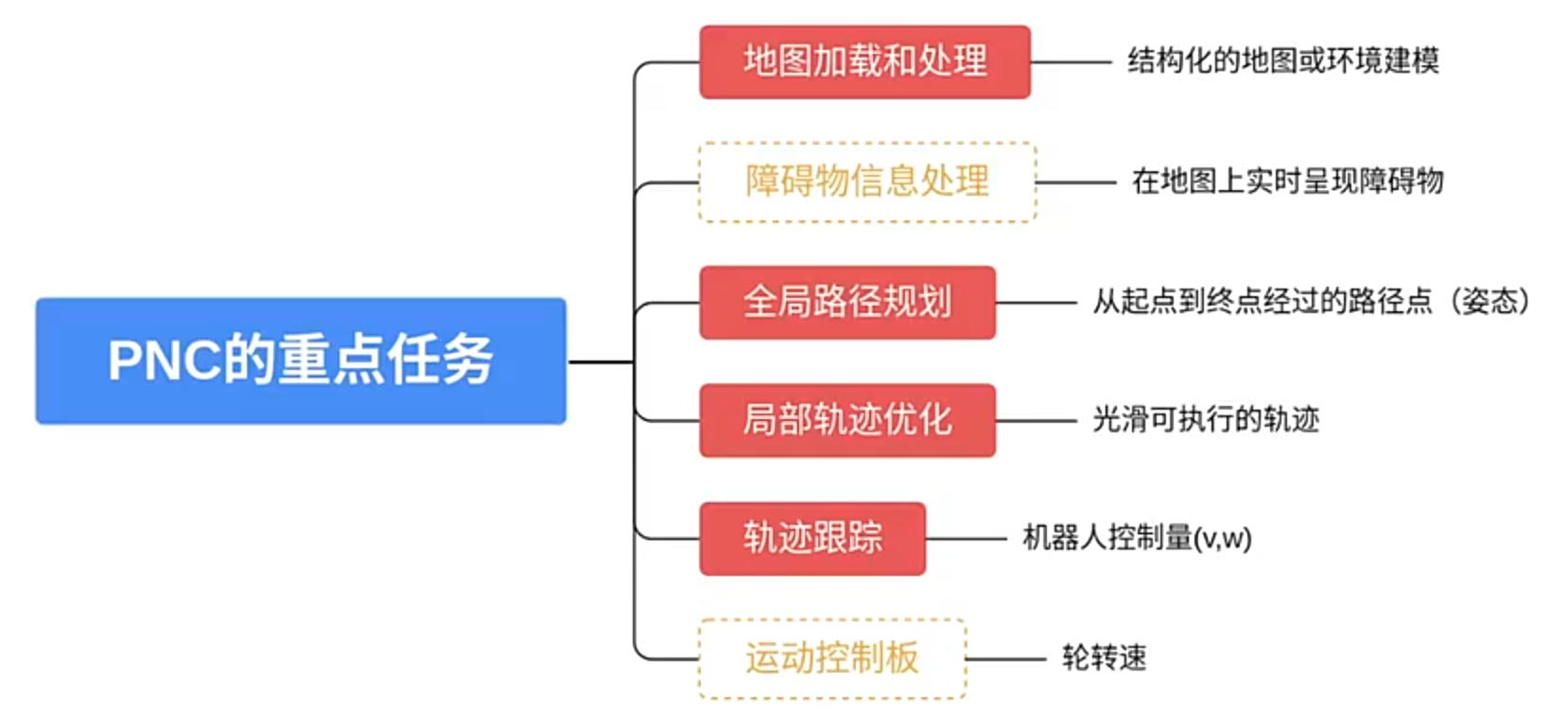
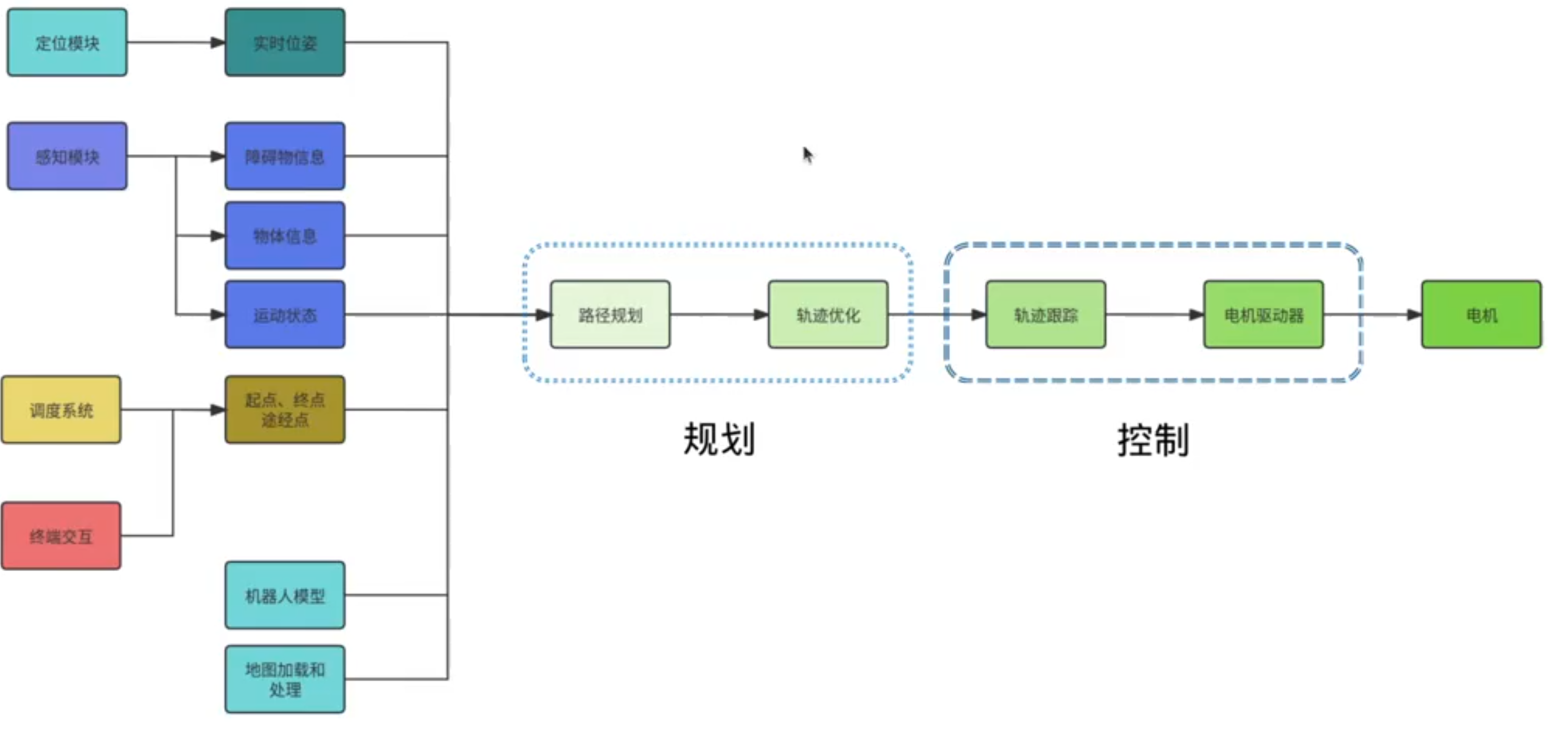

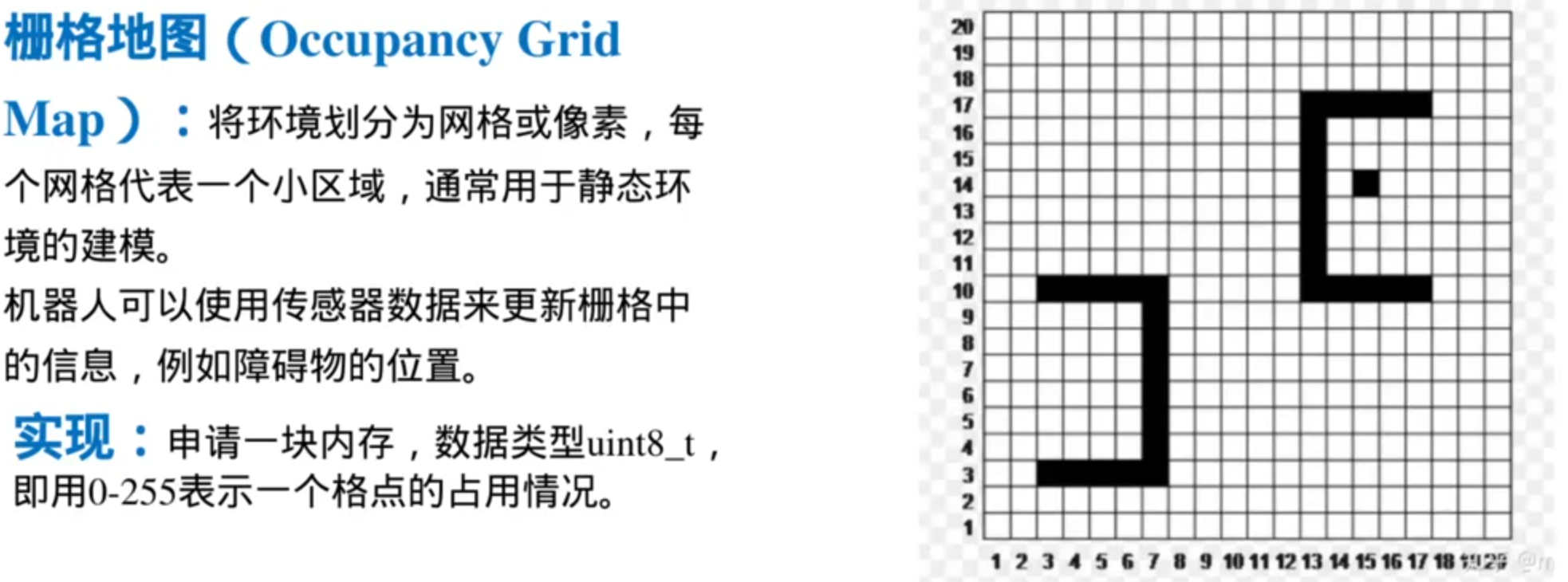
地图处理:
Octree Map存储效率高,占用内存小,适合三维空间
缺点:构建和查询比较复杂,需要递归操作
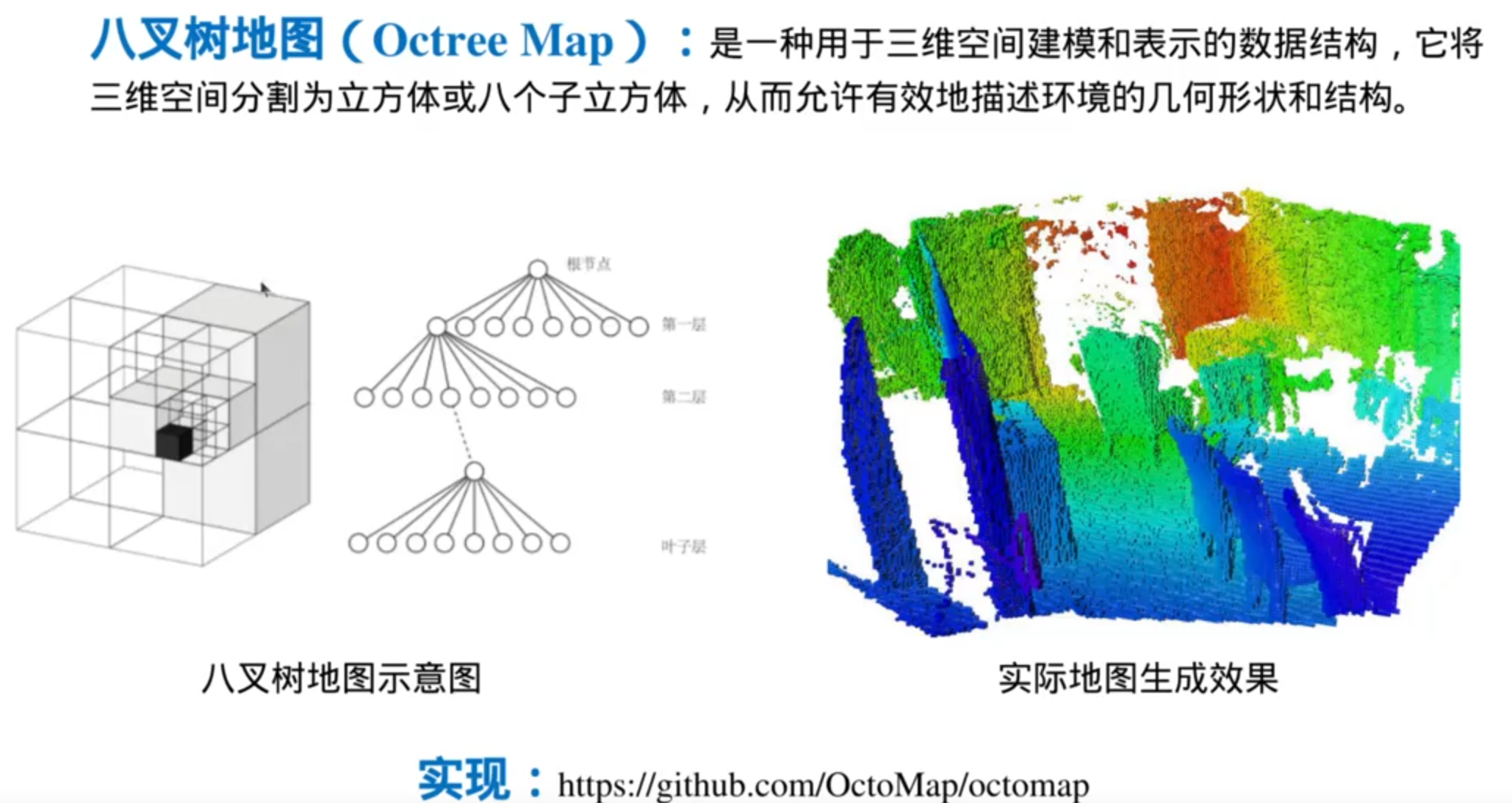
对于平面,可以使用四叉树地图
拓扑地图
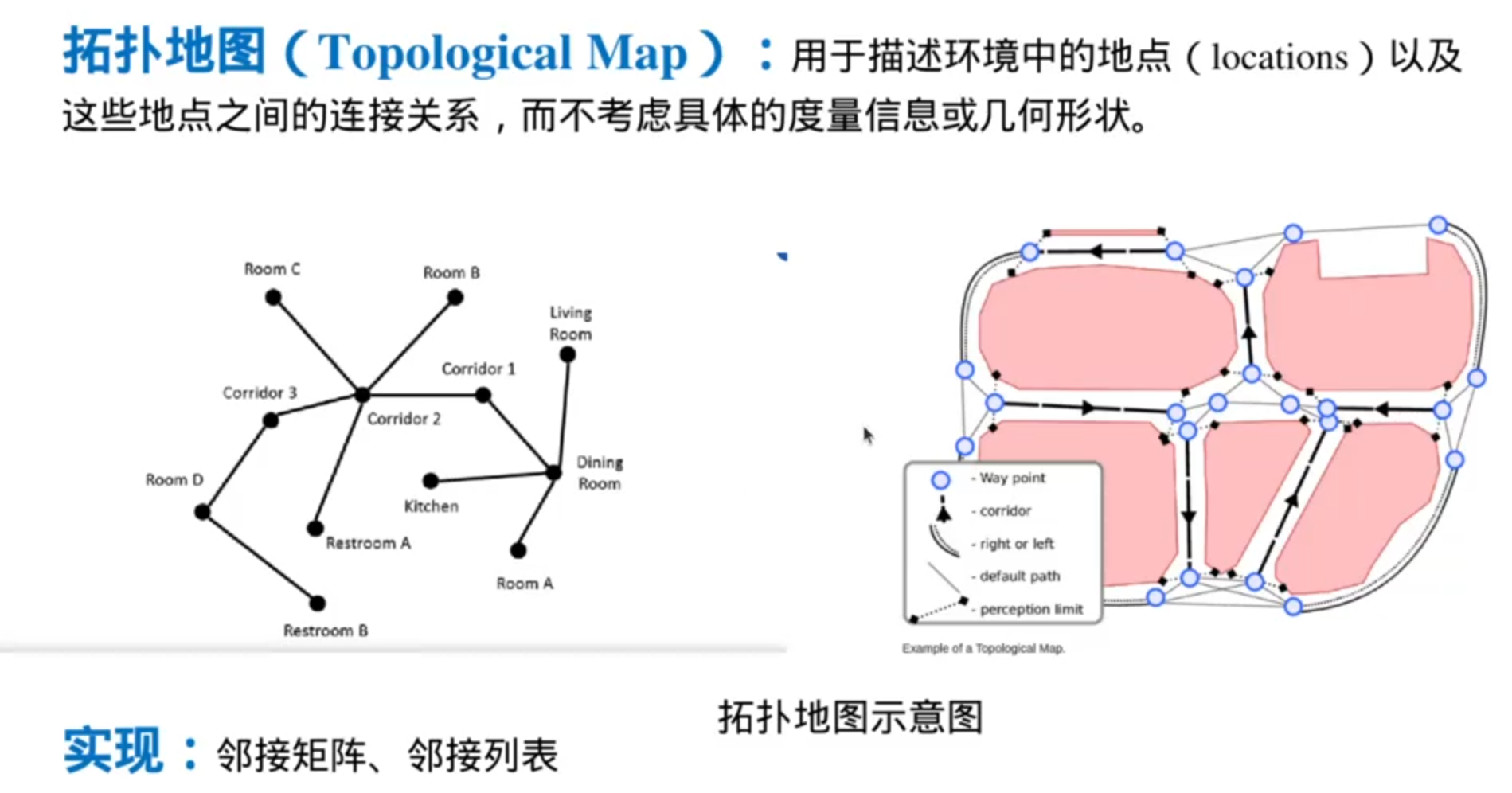
不能生成具体的路径
欧式距离场地图

每一个像素点的值是到目标点的距离
高精地图+激光雷达:

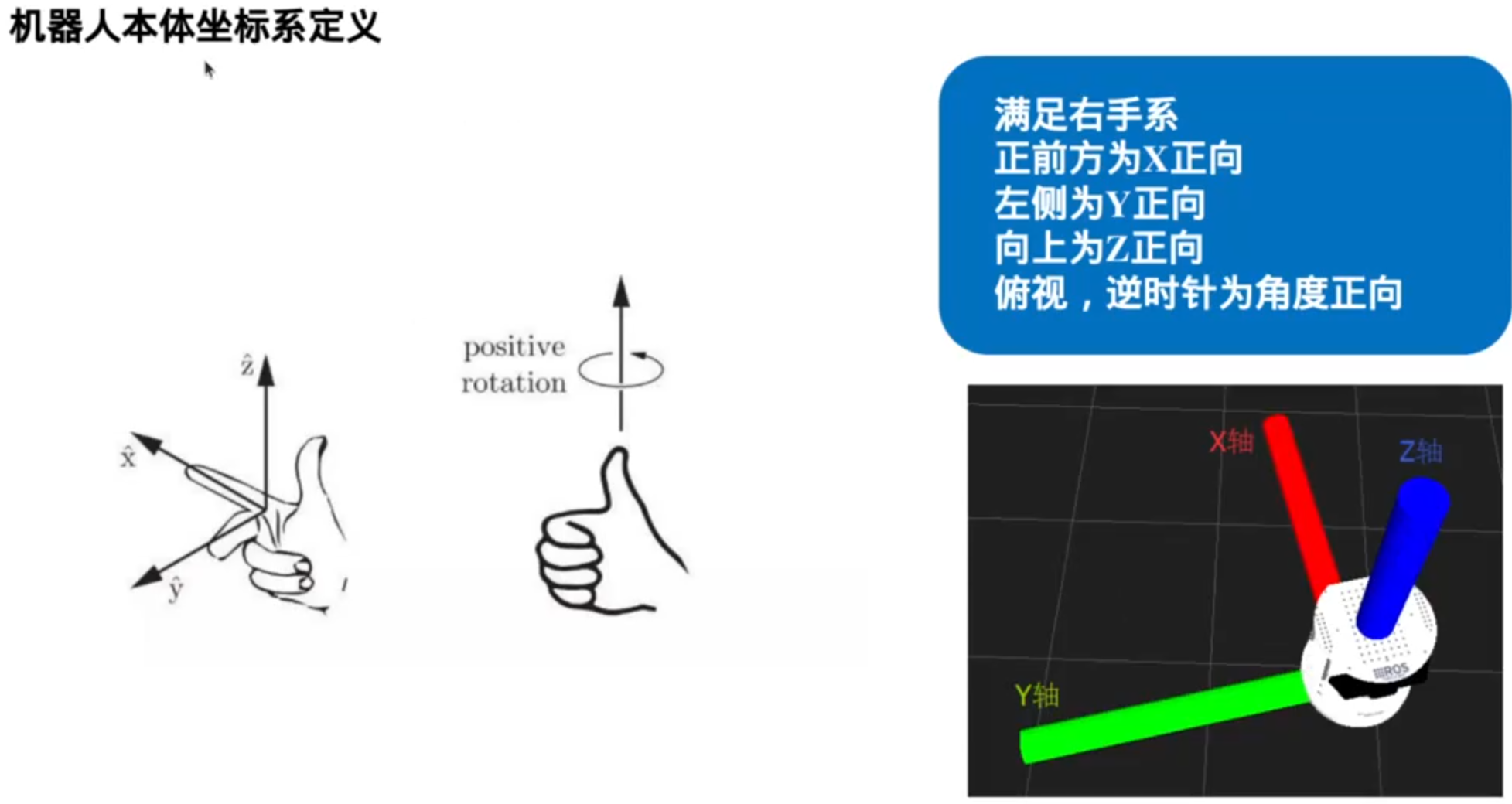
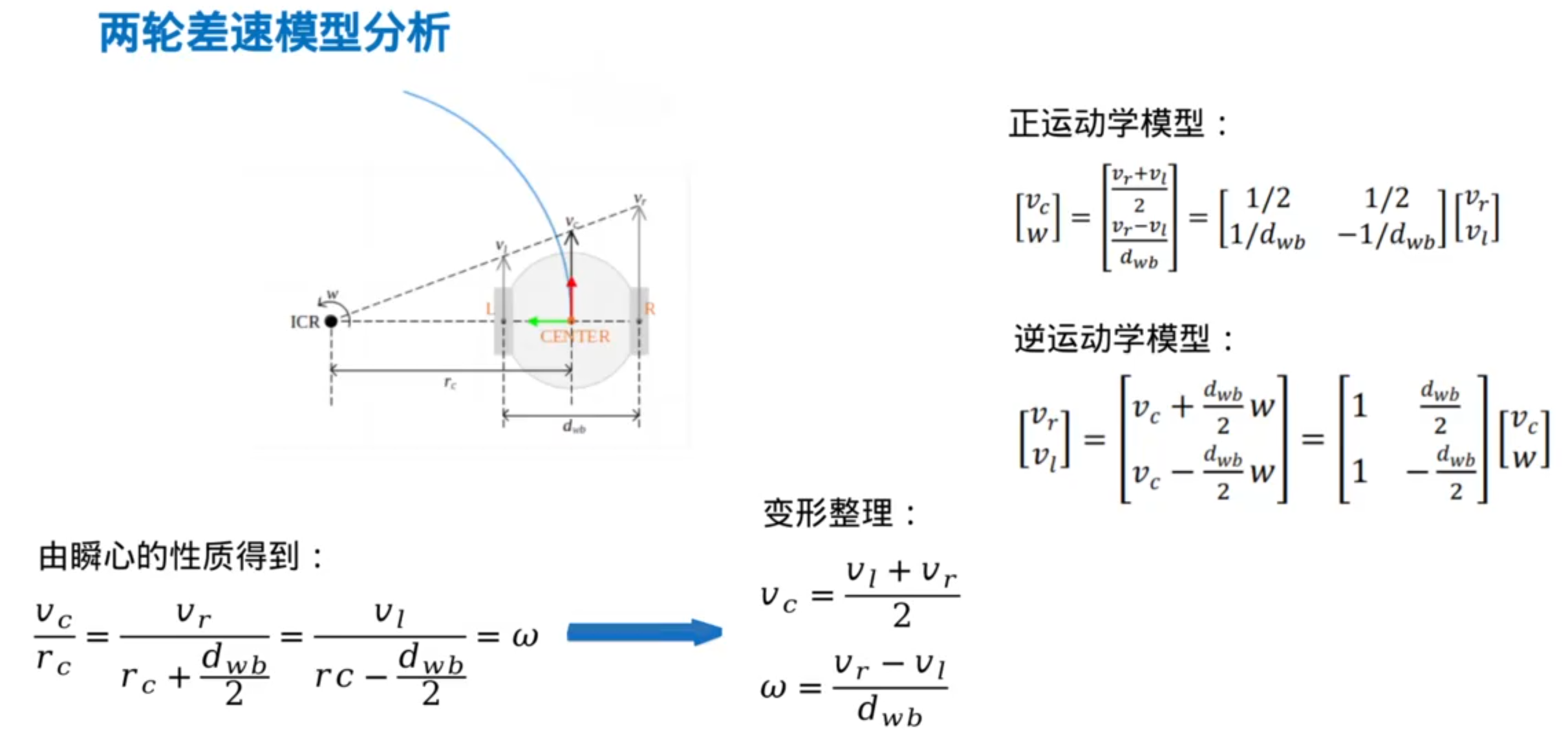
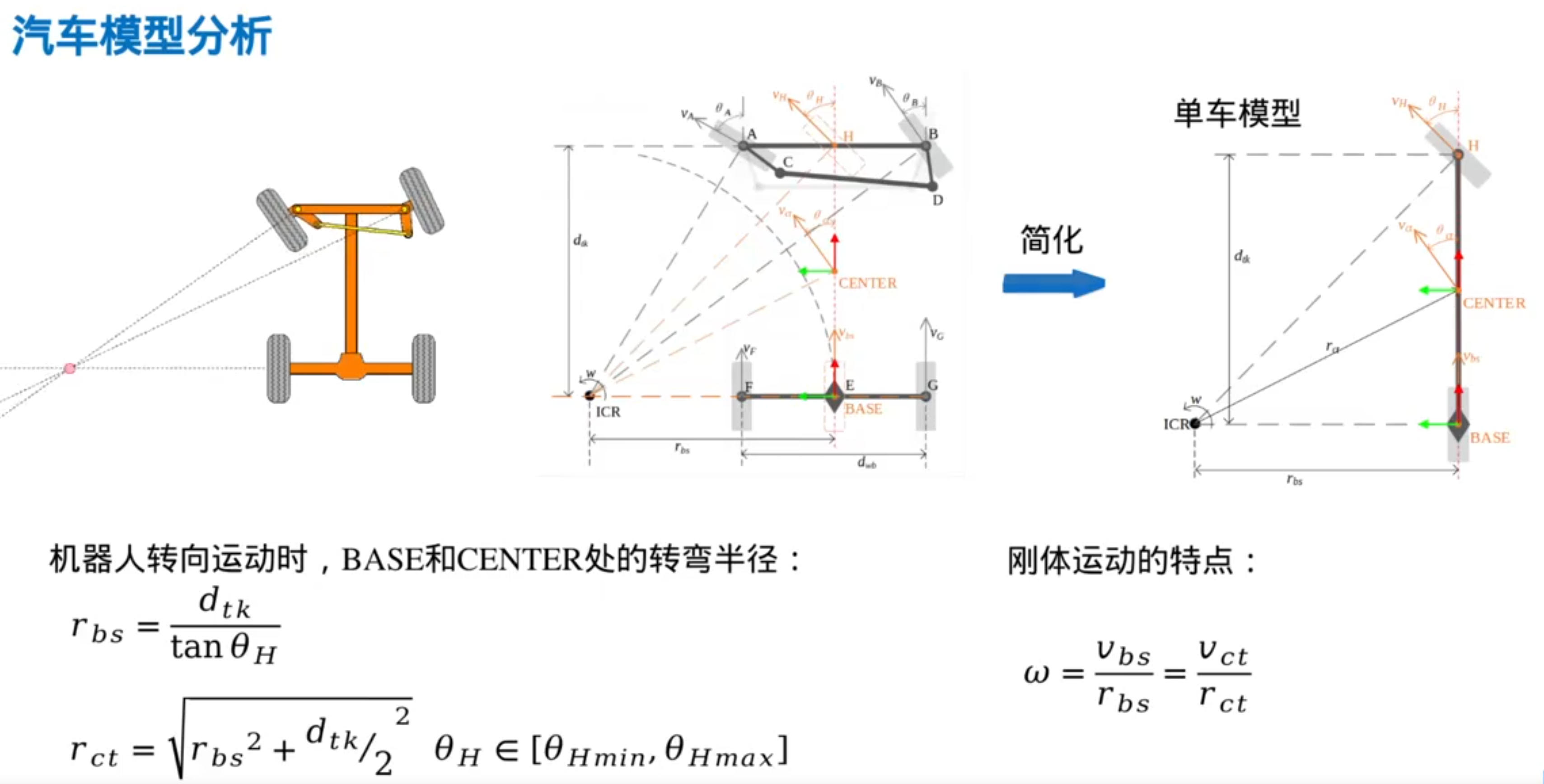
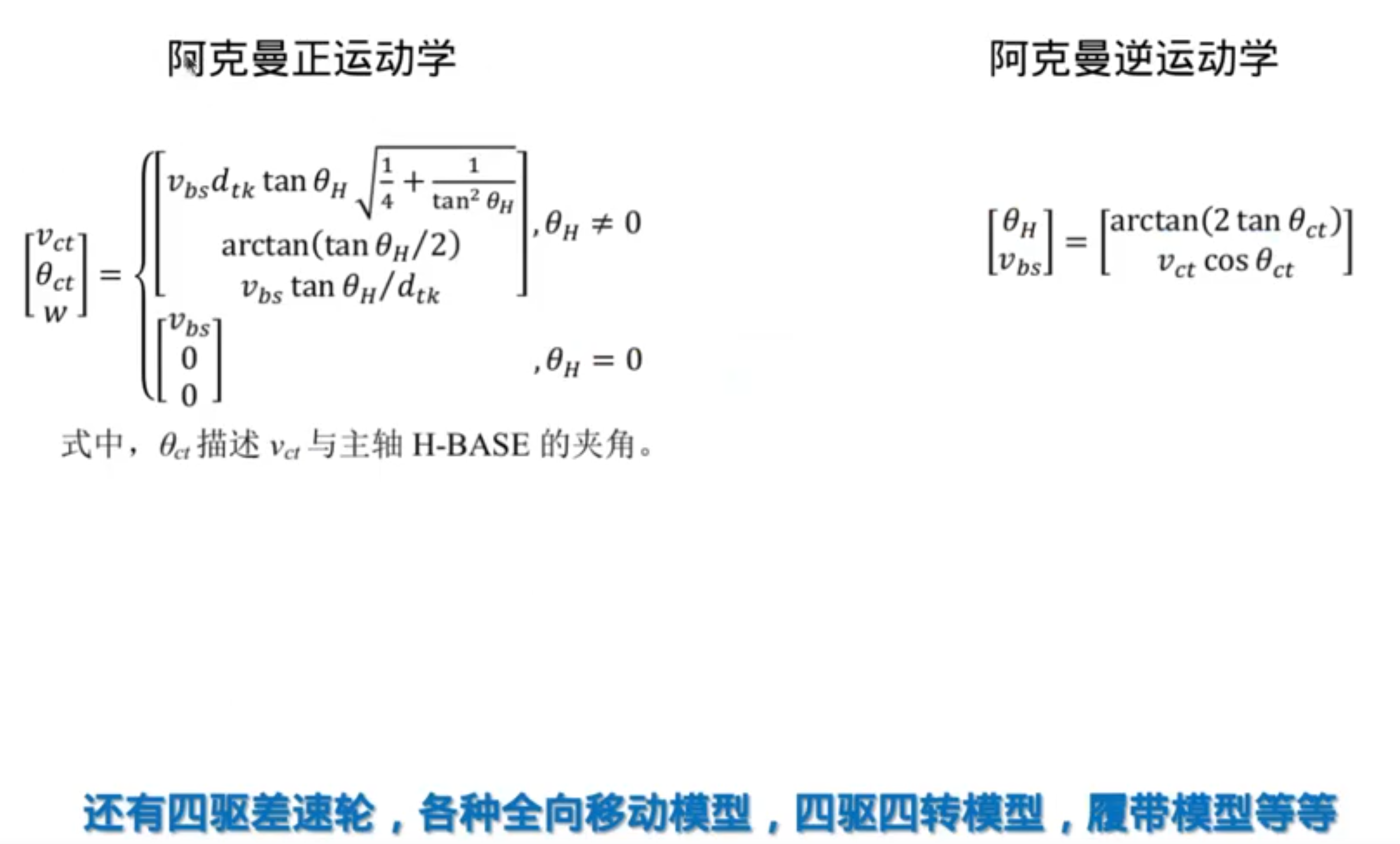
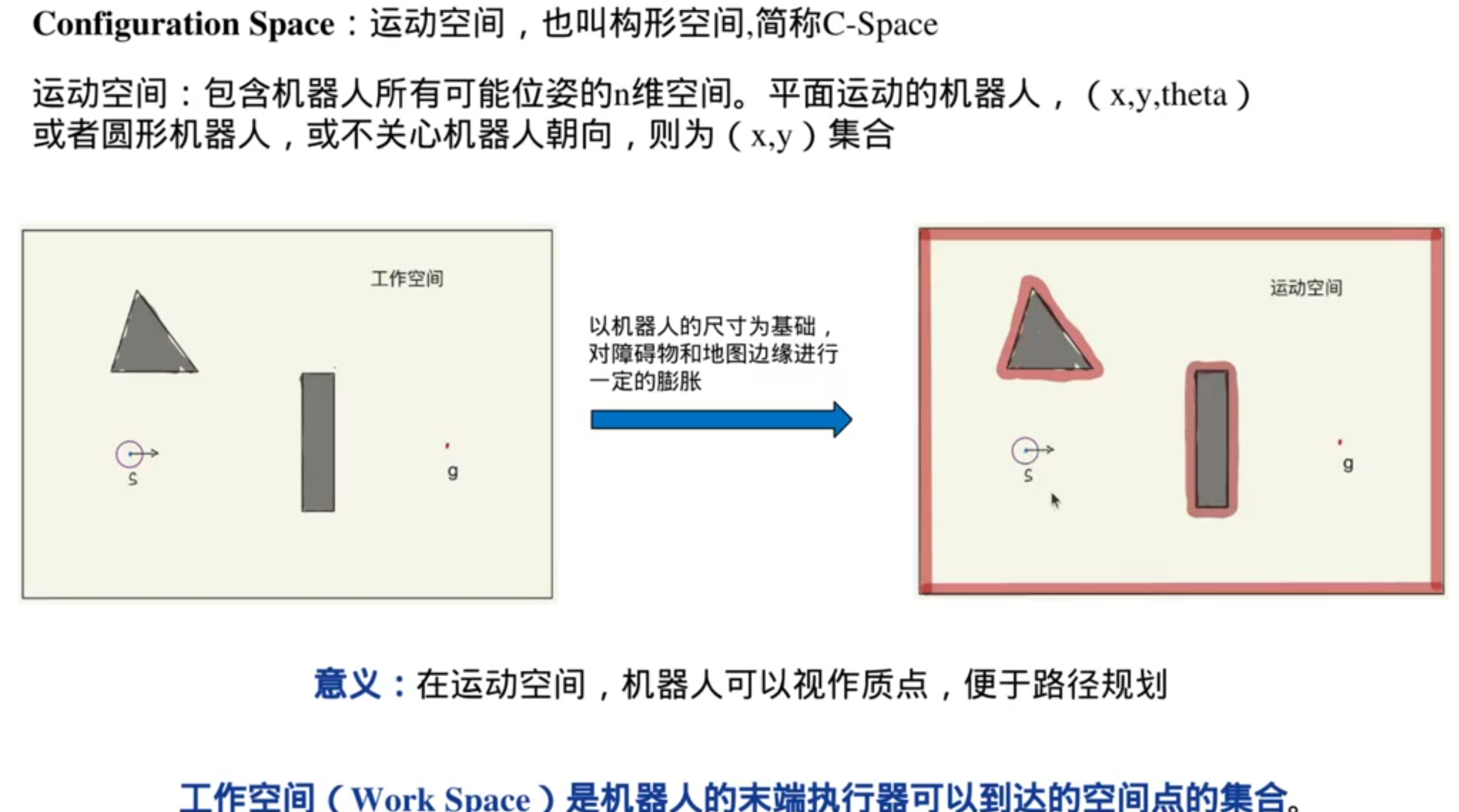
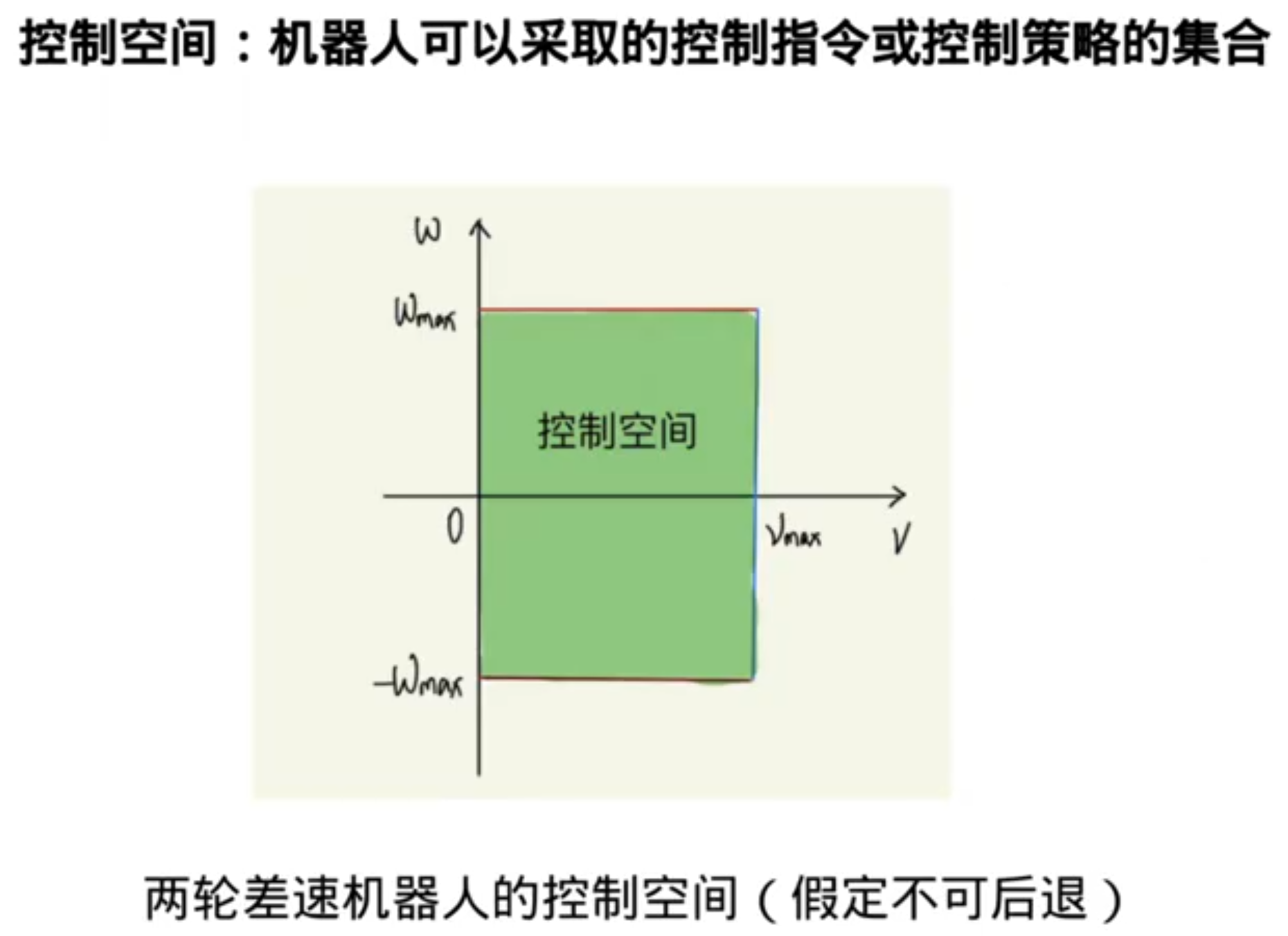
基于结构化地图(已经使用数据结构/储存方式存储好了环境信息)的搜索:

基于采样的路径搜索算法(不太适用于移动机器人)
没有地图的算法:概率路图
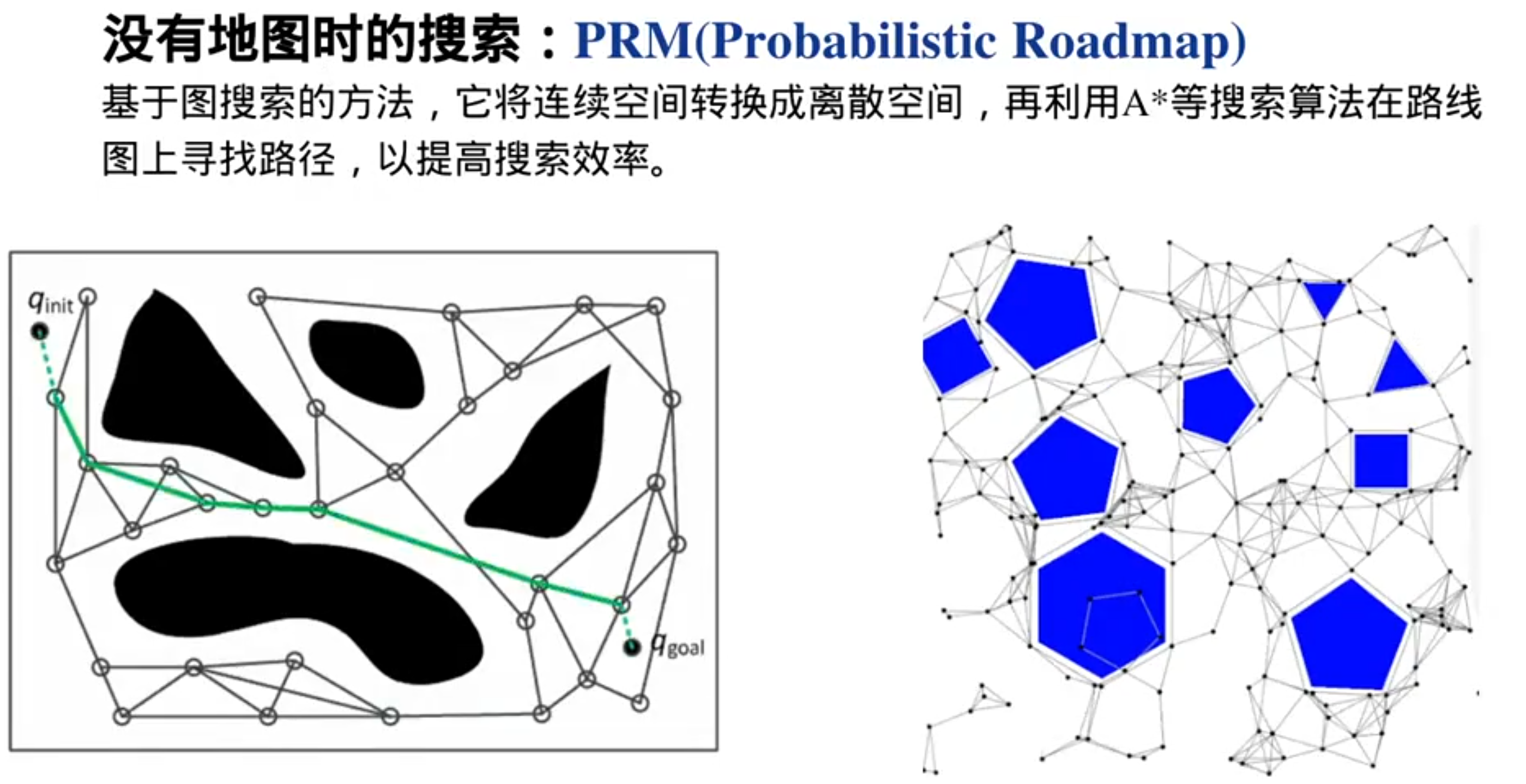

没有地图,先构造地图: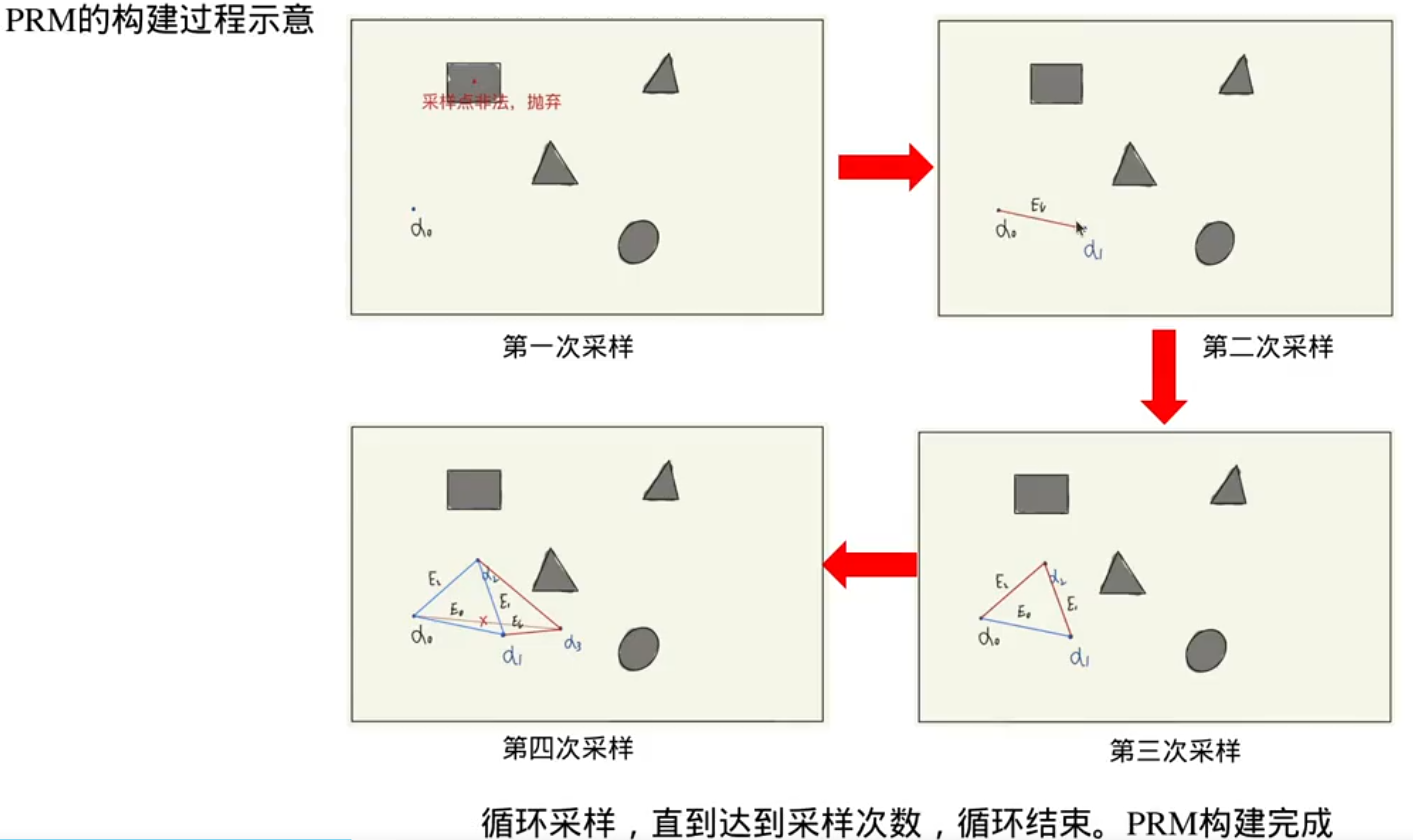
建完图后路径规划:
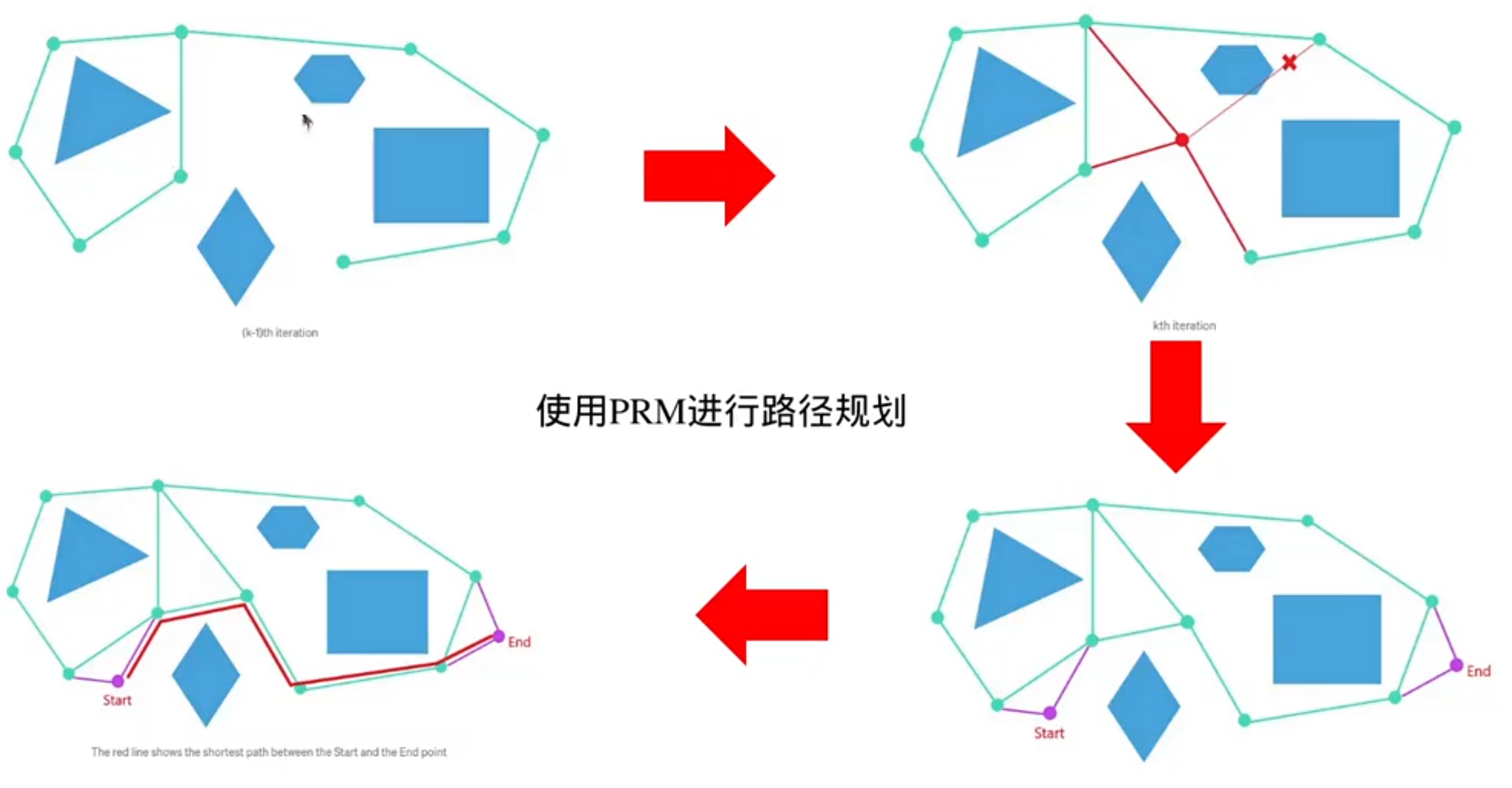


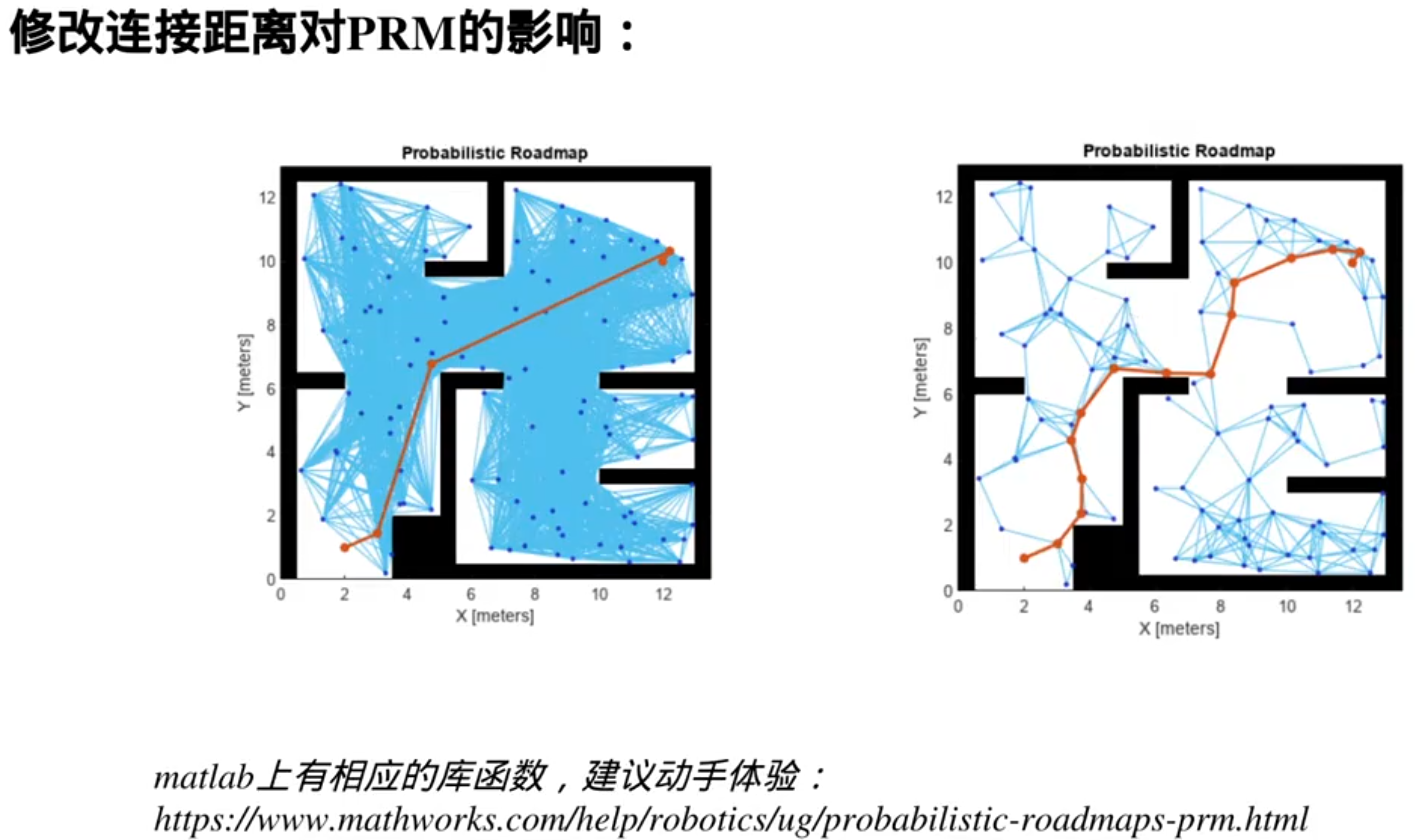
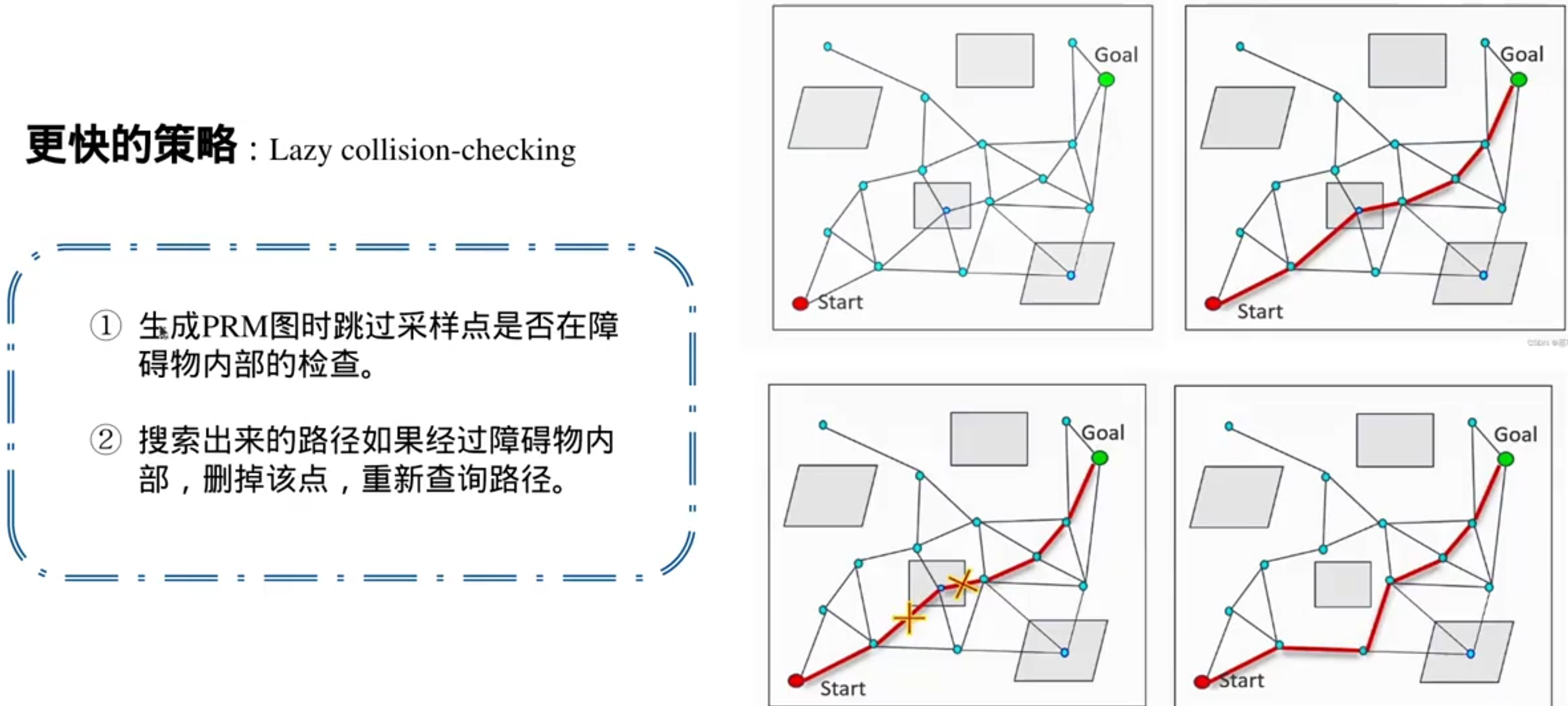
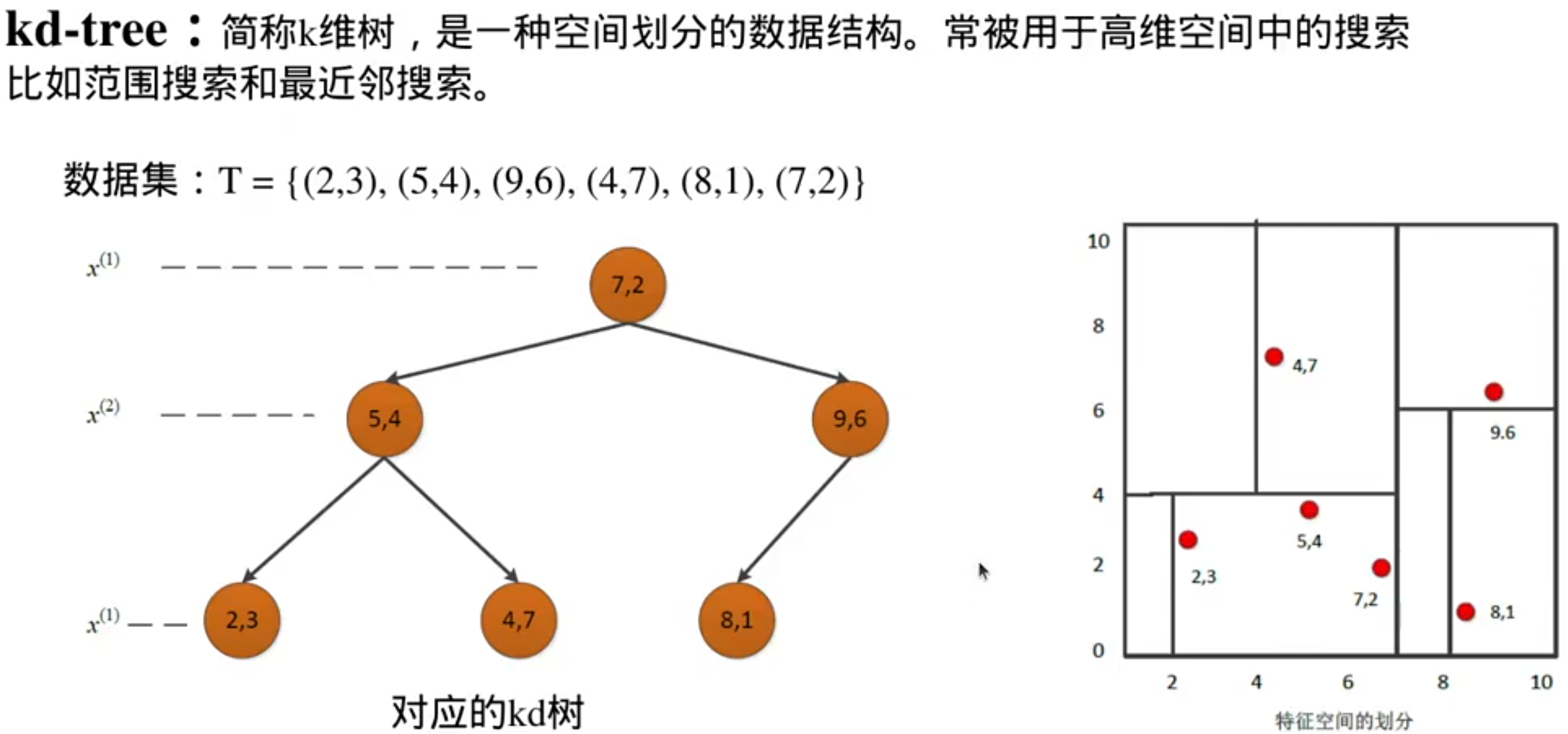
PRM的升级:RRT(快速搜索随机数)
(一边构建地图,一边搜索路径)
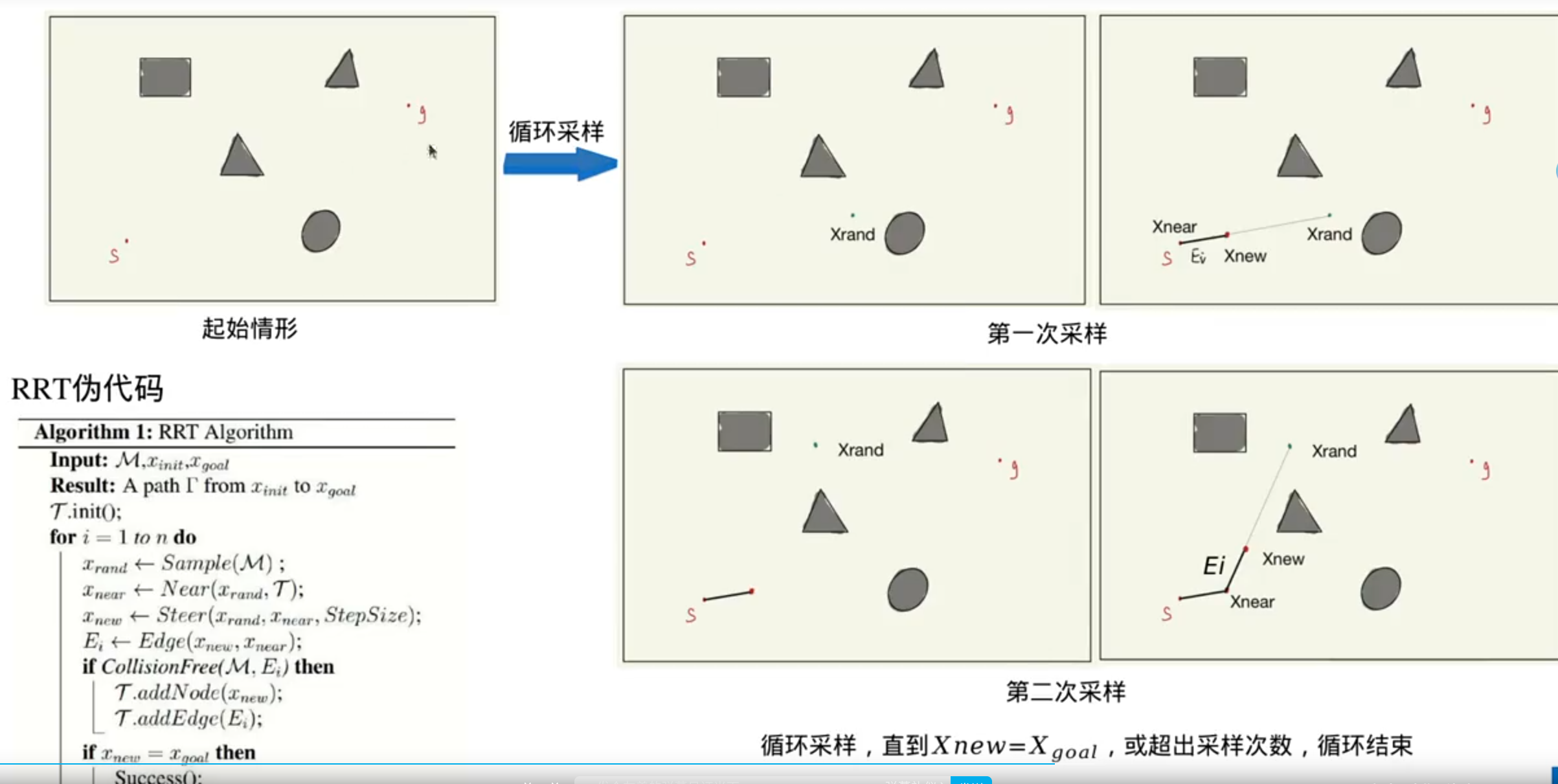


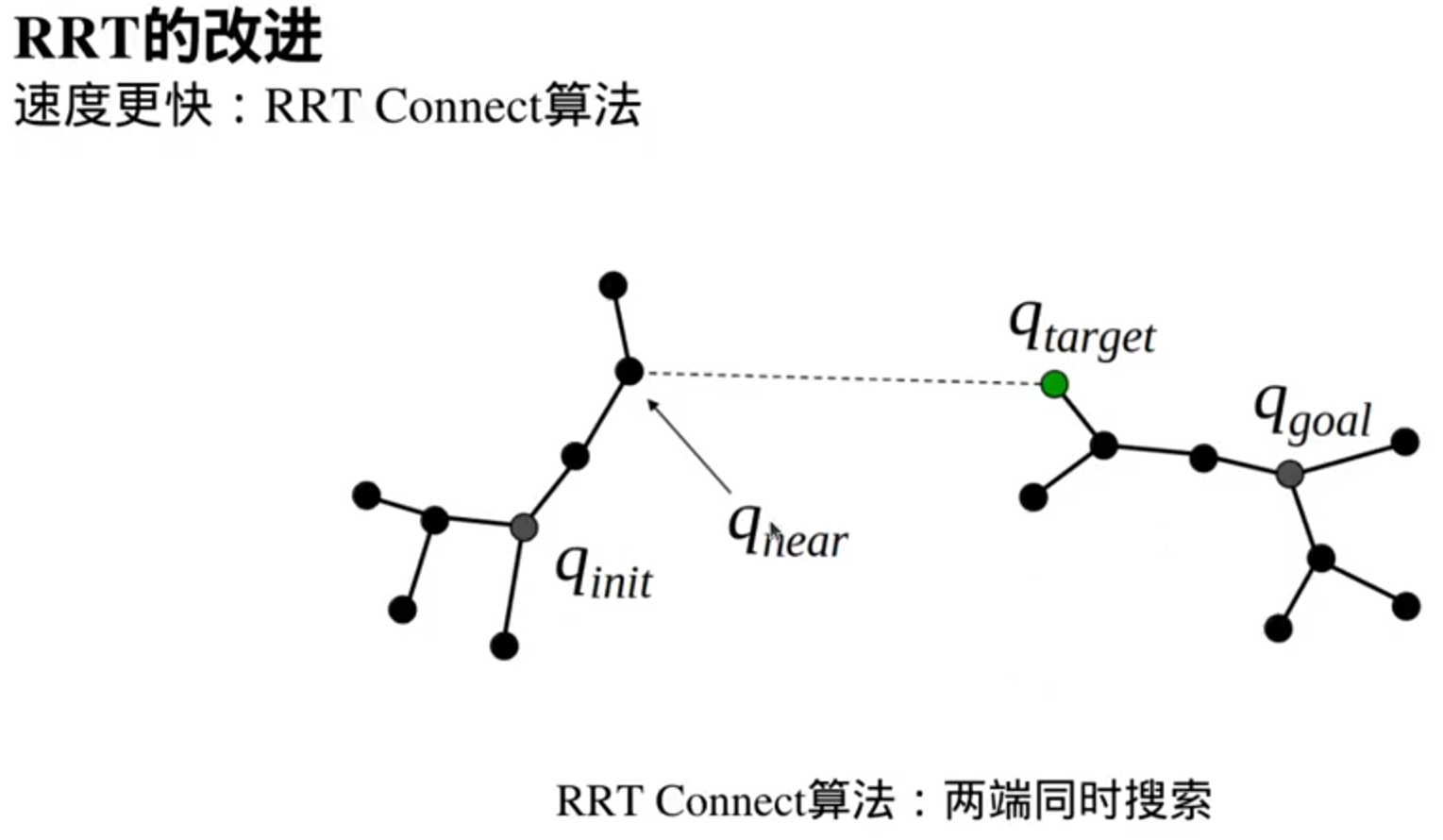

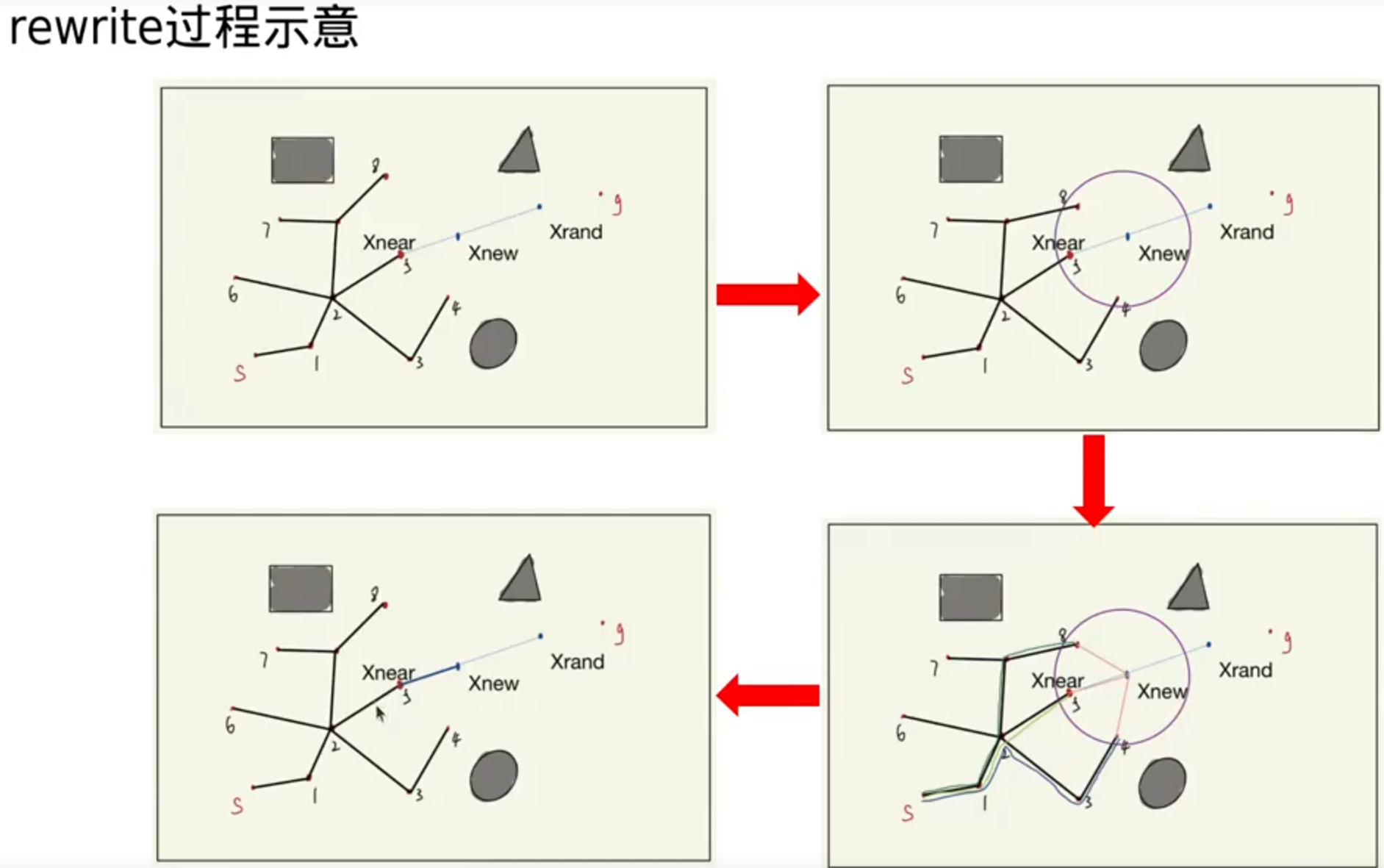
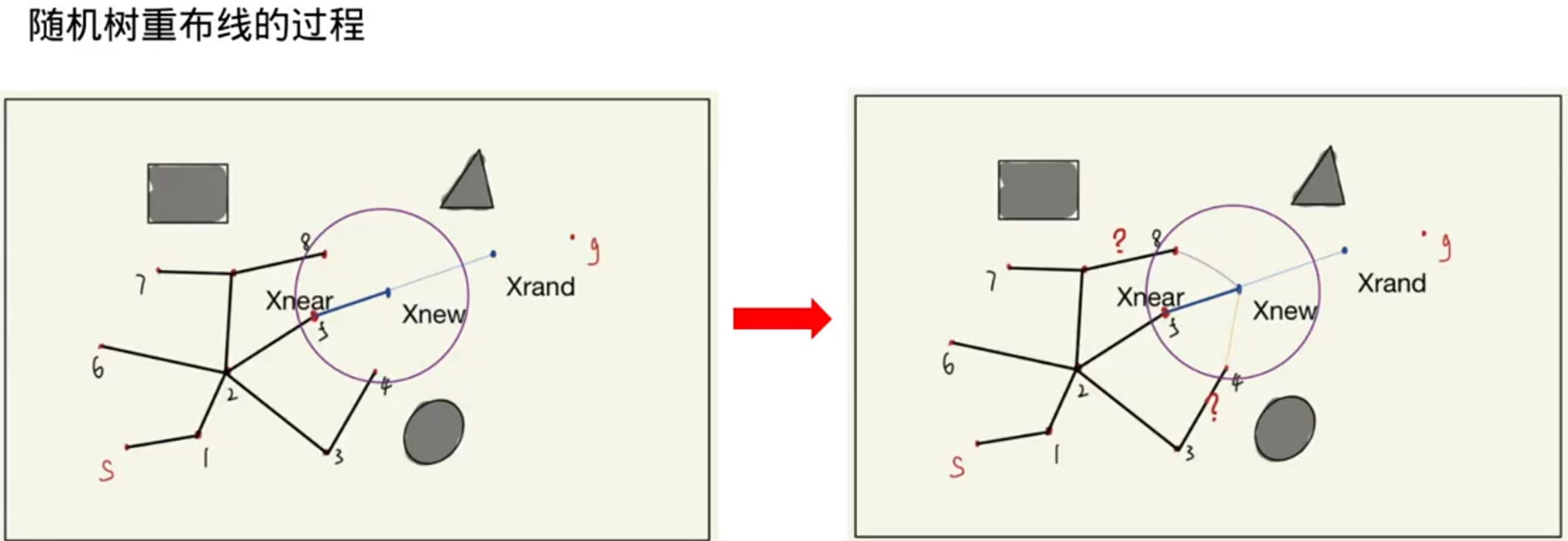
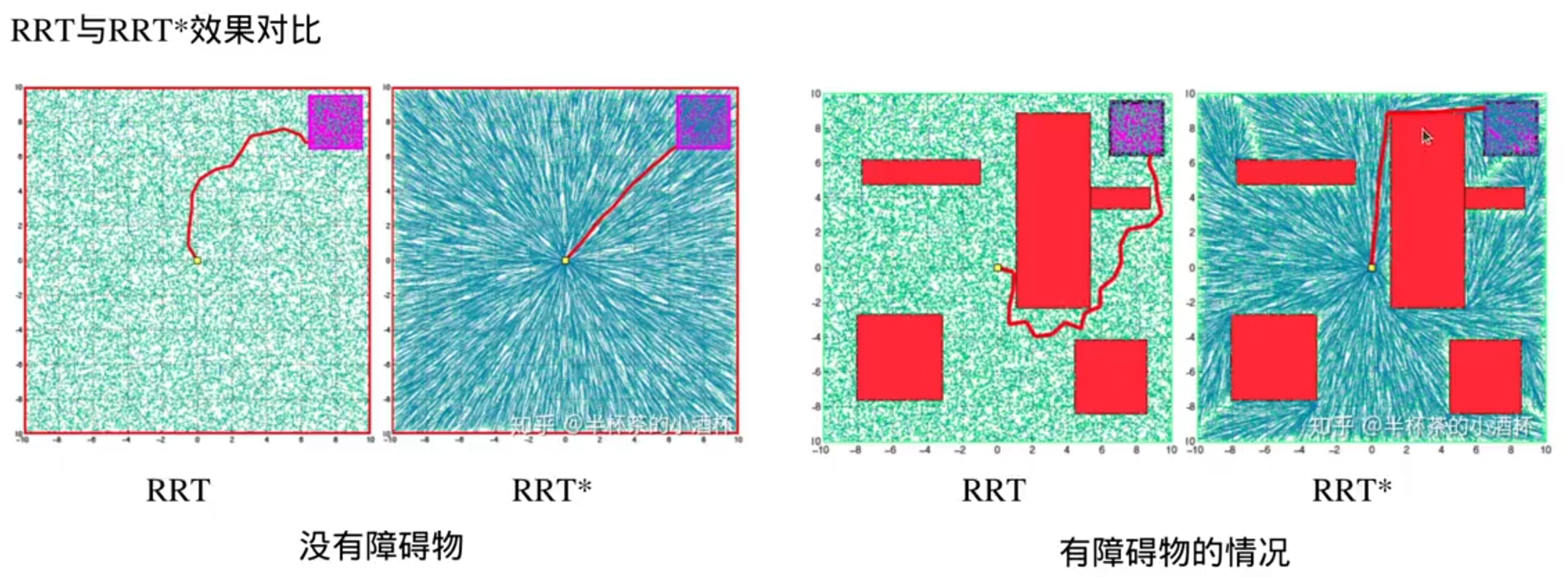
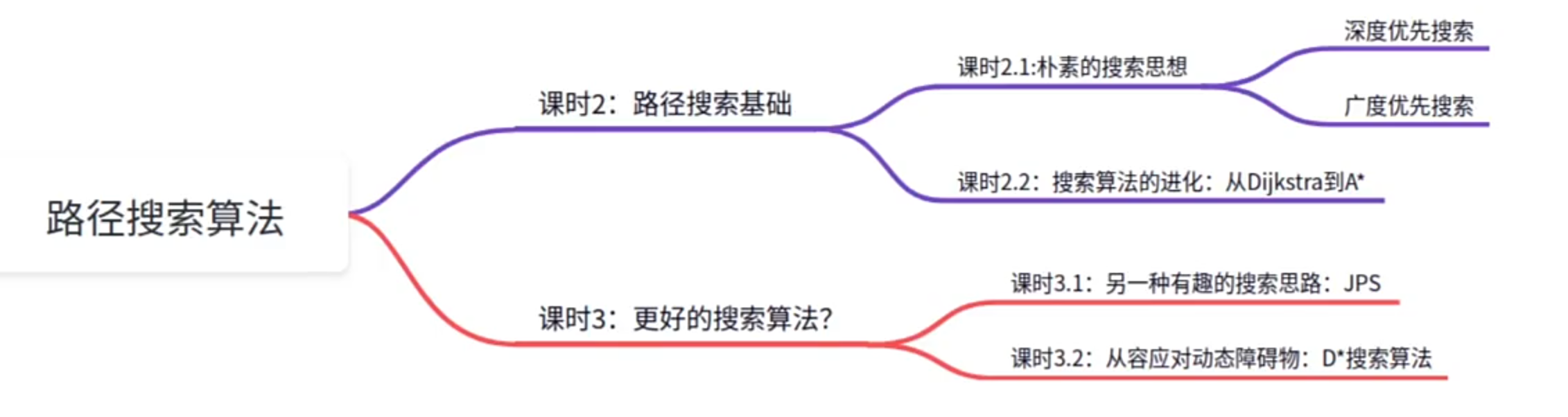
基于图搜索的路径搜索算法
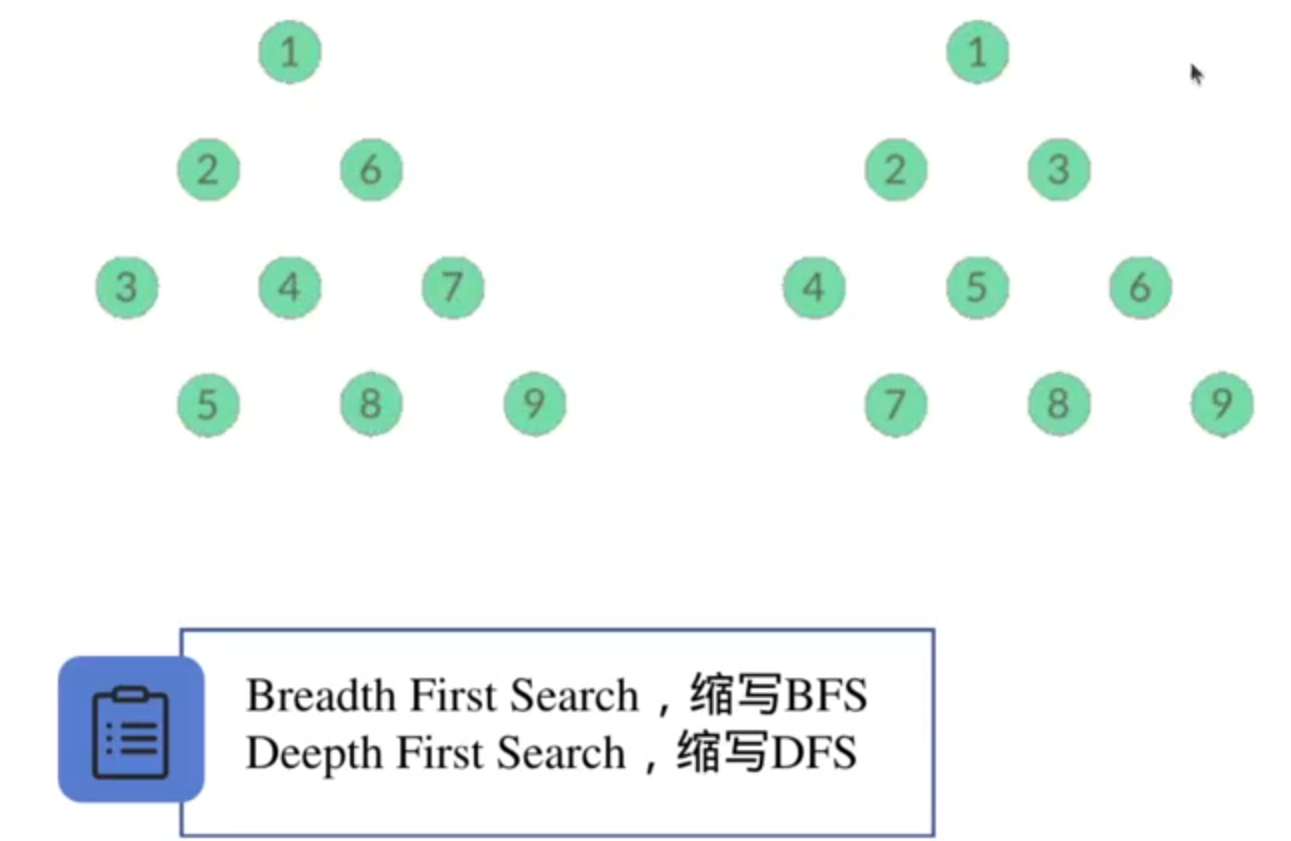
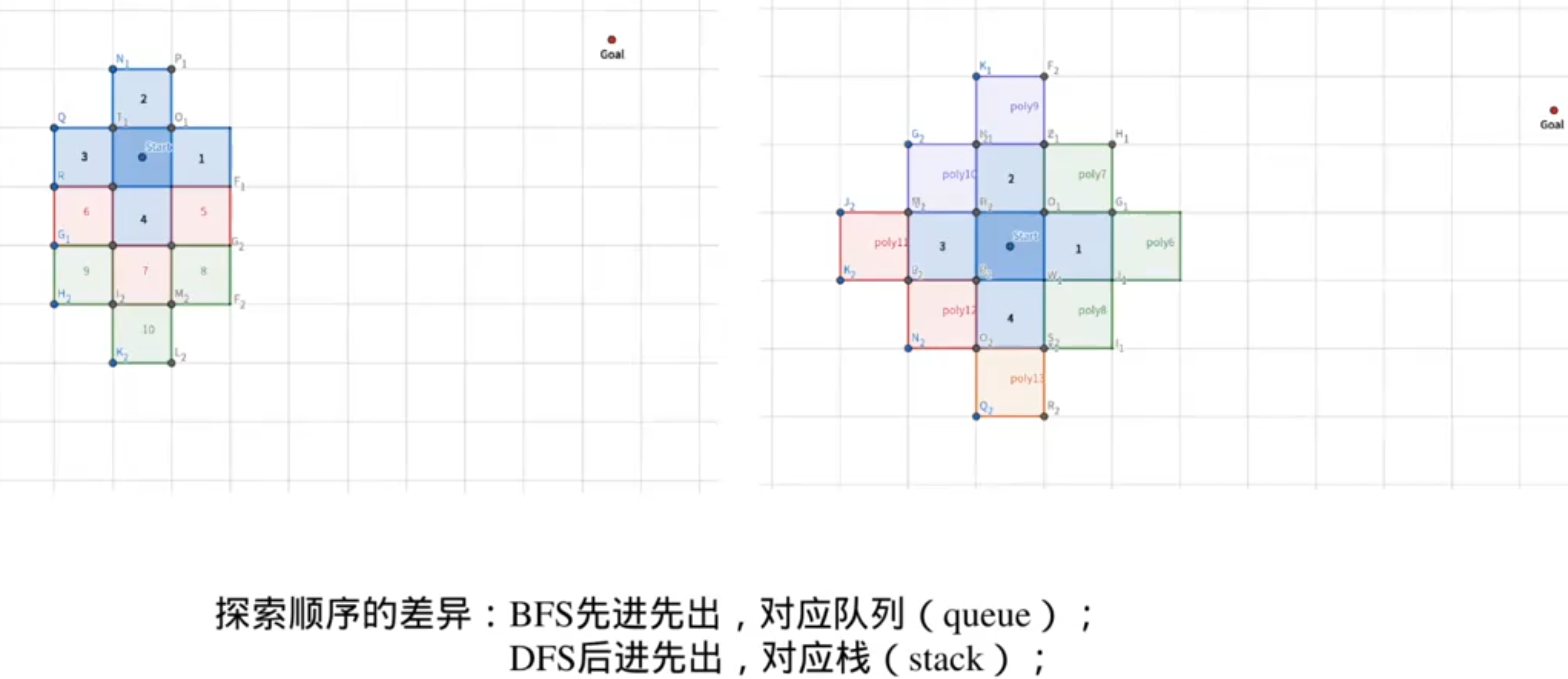
1.朴素的搜索思想——BFS,DFS
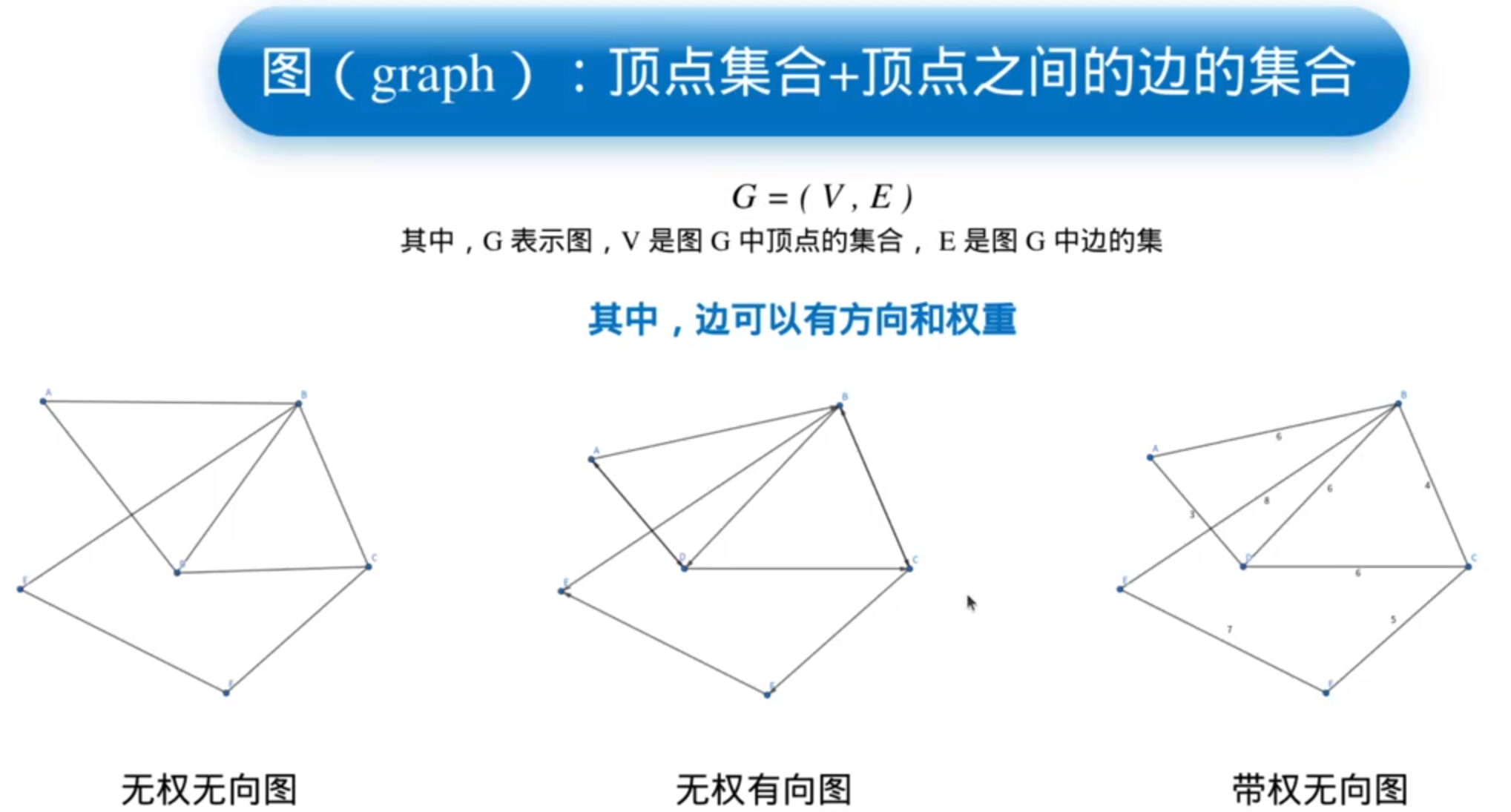
栅格地图可以很容易的转换成graph,欧式距离场可以很容易的转换成栅格地图,拓扑地图本身就是graph
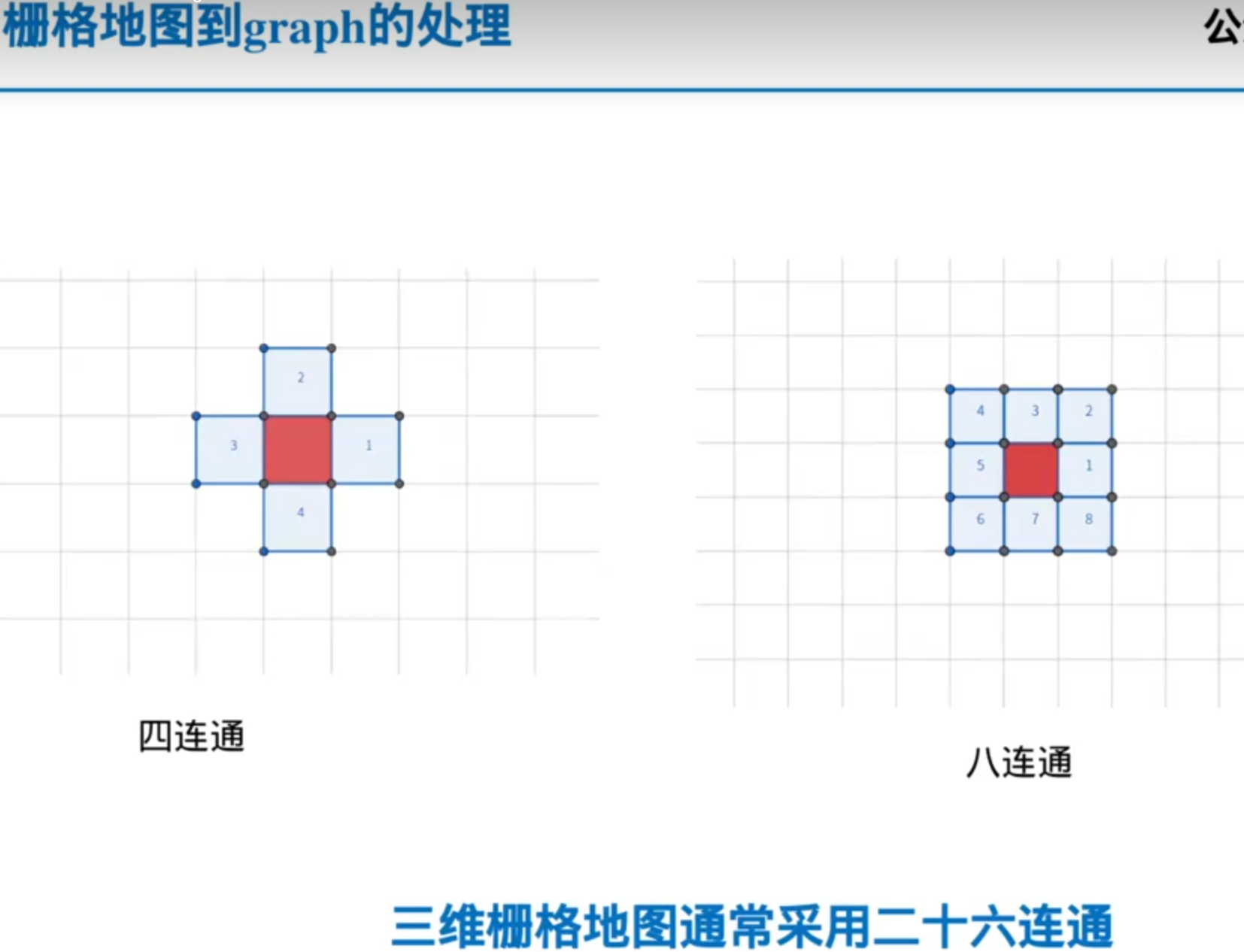
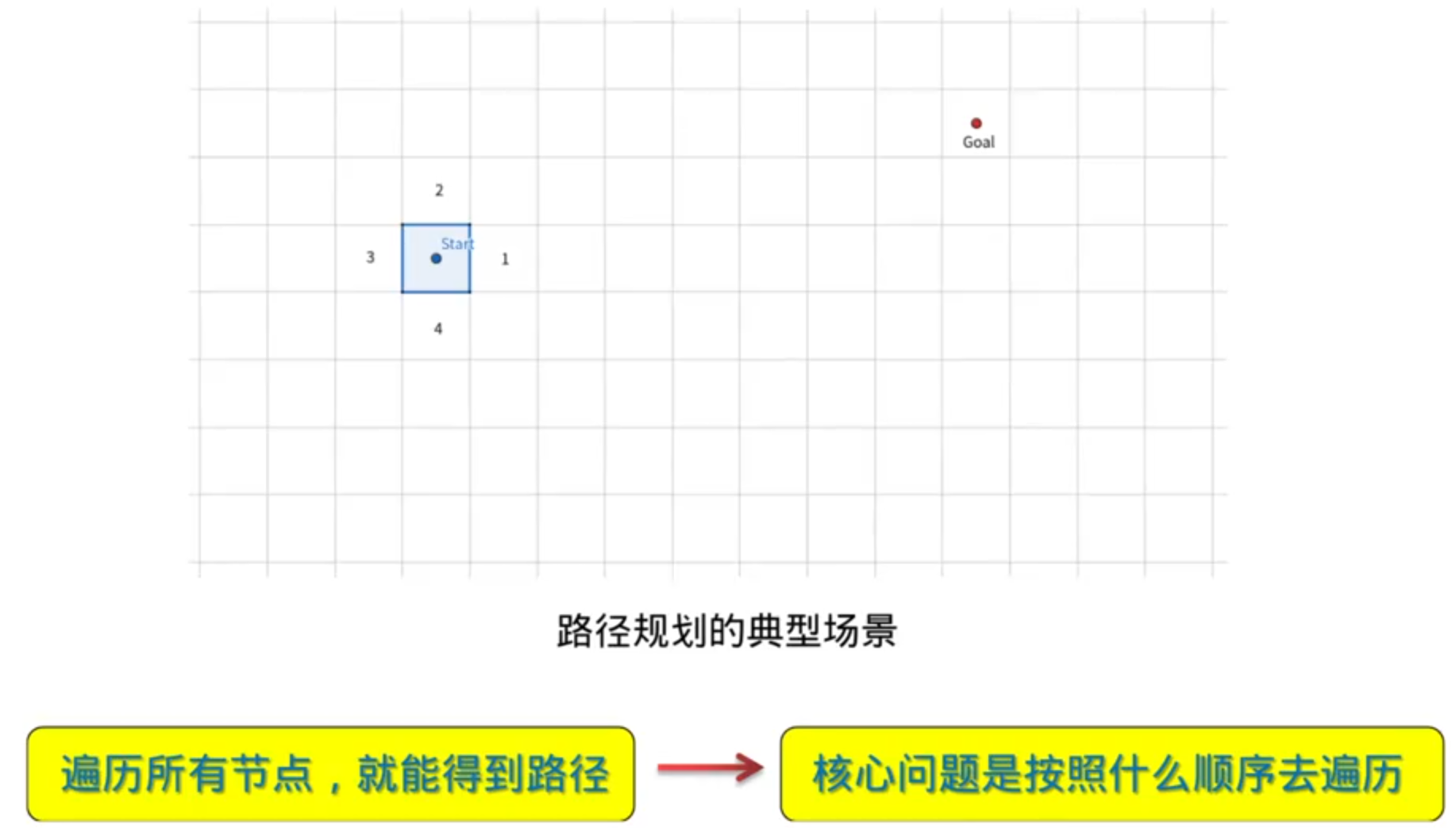
图搜索的核心问题:

std::reverse 是 C++ 标准库中的一个算法,用于反转给定范围内的元素顺序。它定义在 <algorithm> 头文件中。
std::reverse 接受两个迭代器作为参数,表示要反转的范围。其基本语法如下:
#include <algorithm> // 需要包含这个头文件
#include <vector>
#include <iostream>
int main() {
std::vector<int> vec = {1, 2, 3, 4, 5};
// 反转 vec 中的元素
std::reverse(vec.begin(), vec.end());
// 输出反转后的结果
for (int v : vec) {
std::cout << v << " "; // 输出: 5 4 3 2 1
}
return 0;
}
2.(DFS,BFS)搜索算法的进化————Dijkstra,A*
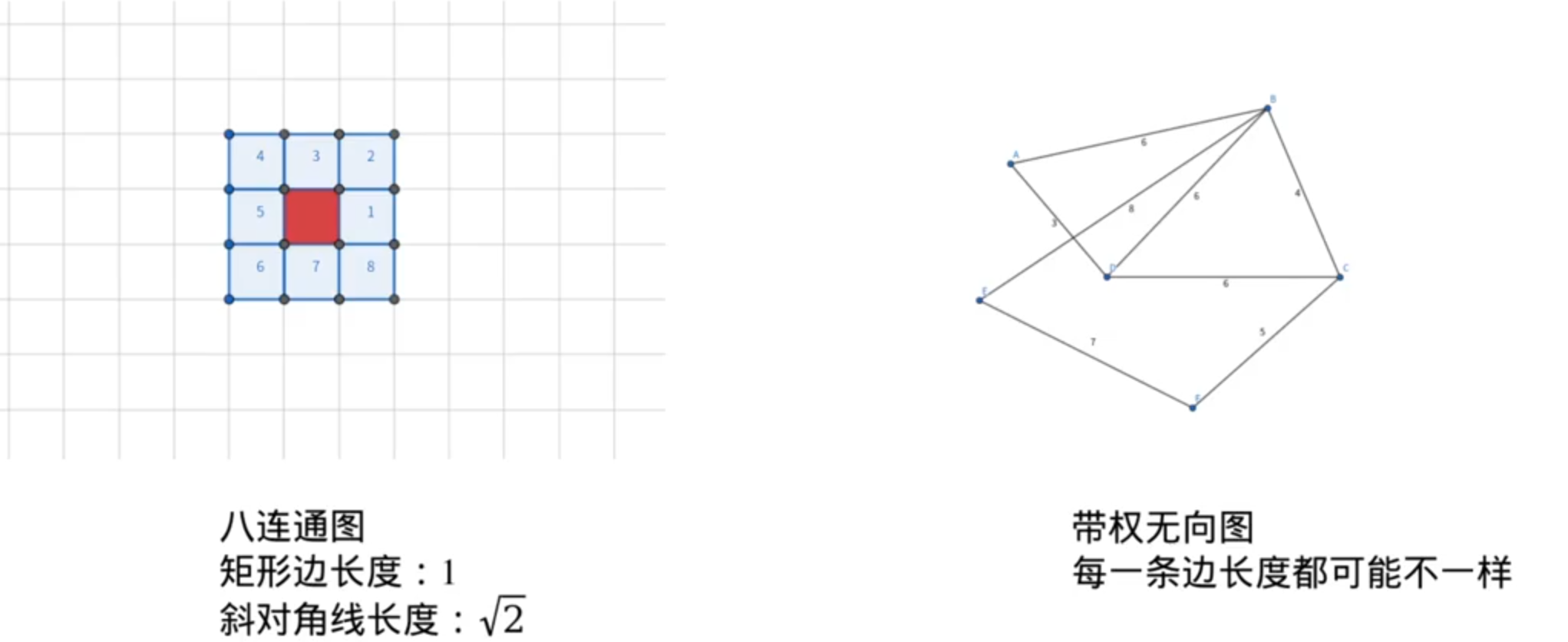
Dijkstra(使用八联通图,可以走斜线)

为什么: 如果distance._current大于distance[current]: 继续下一次循环
优先队列会按照节点的最小距离进行排序。可能在多个阶段,一个节点被加入队列,但这些加入可能是基于旧的距离值。
当我们从队列中弹出一个节点时,这个节点的距离可能并不是它的最短距离(因为它可能已经被更短的路径更新过)。
如果当前弹出的节点的距离大于我们在
distance数组中记录的最短距离,这意味着我们已经找到了一条更短的路径到达这个节点,因此可以跳过对这个节点的处理。
A*(优化搜索速度)
A*的核心思想:不但考虑七点到当前节点的代价值,还要考虑当前节点到目标点的代价值
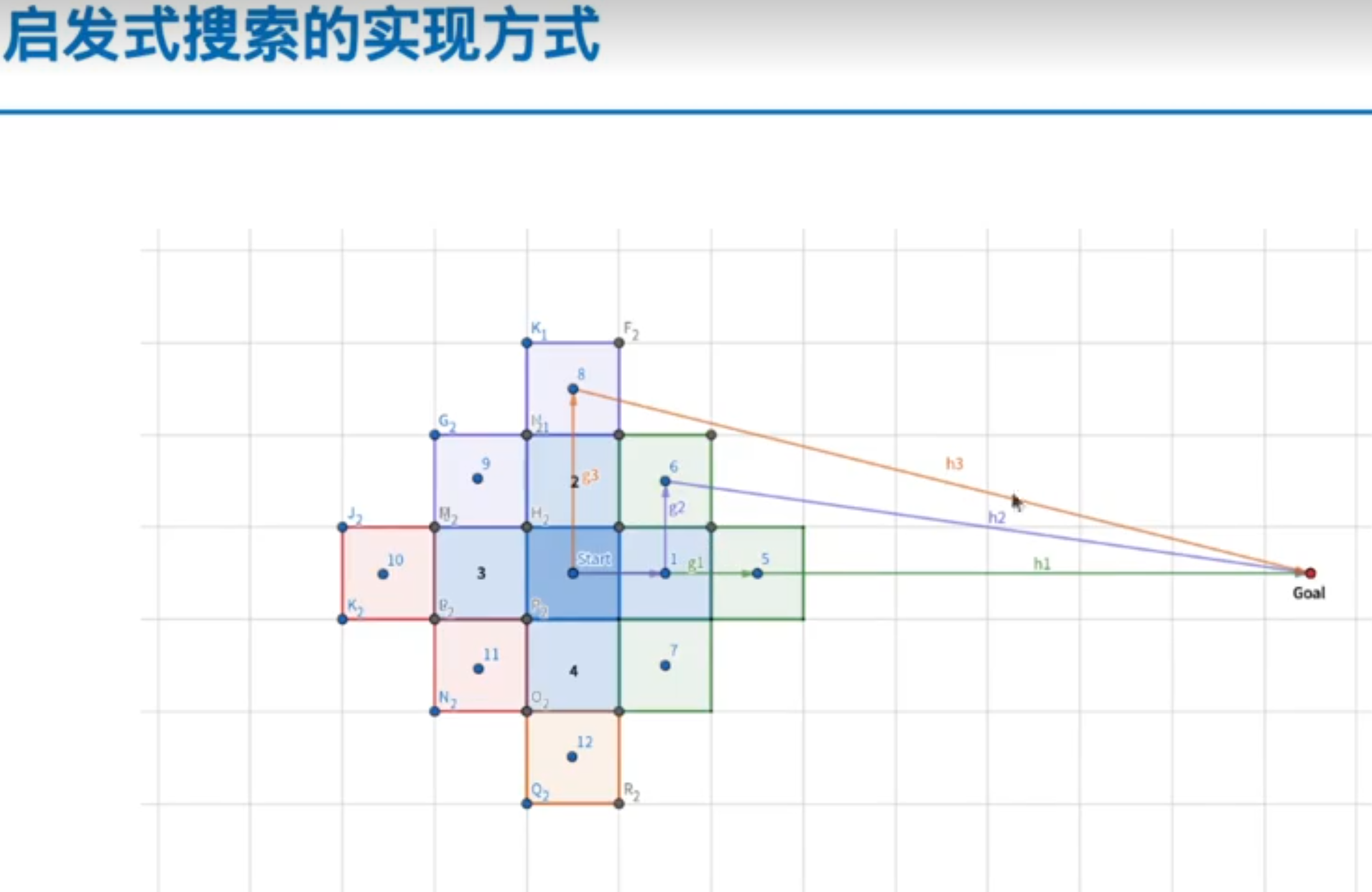
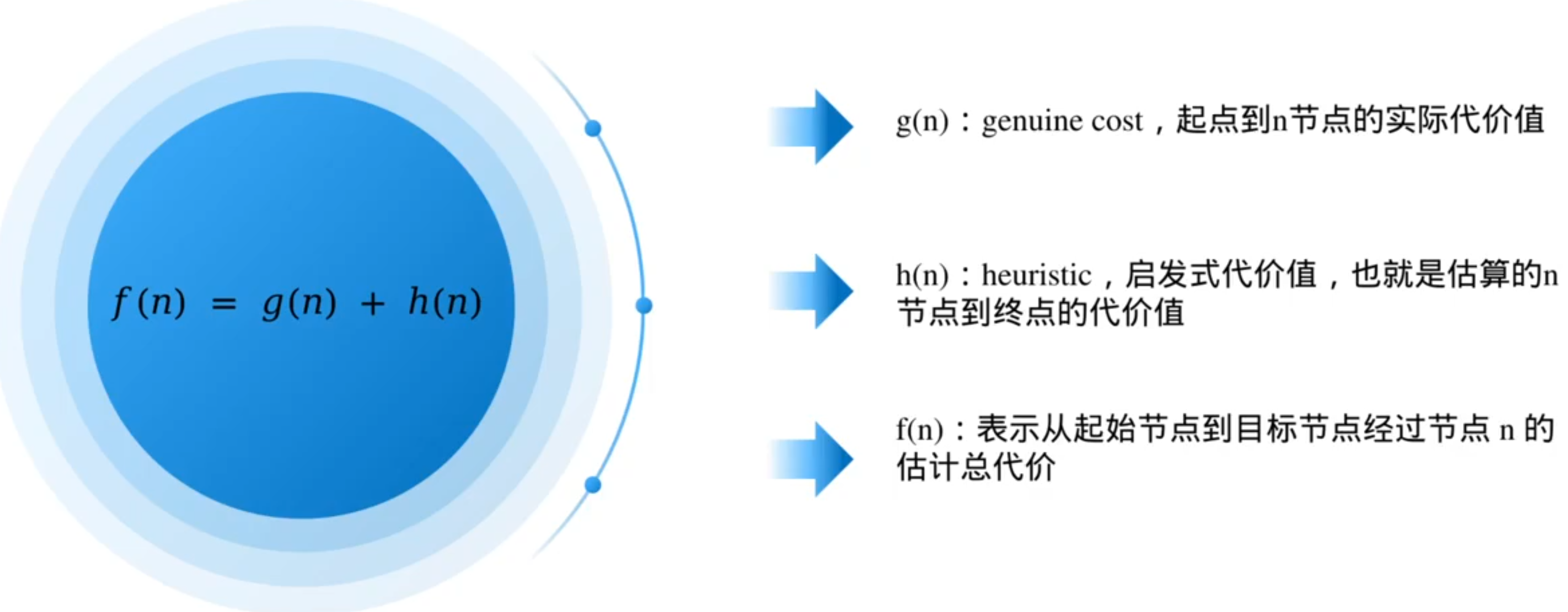
这里的估算函数叫启发式函数
常用的启发式函数
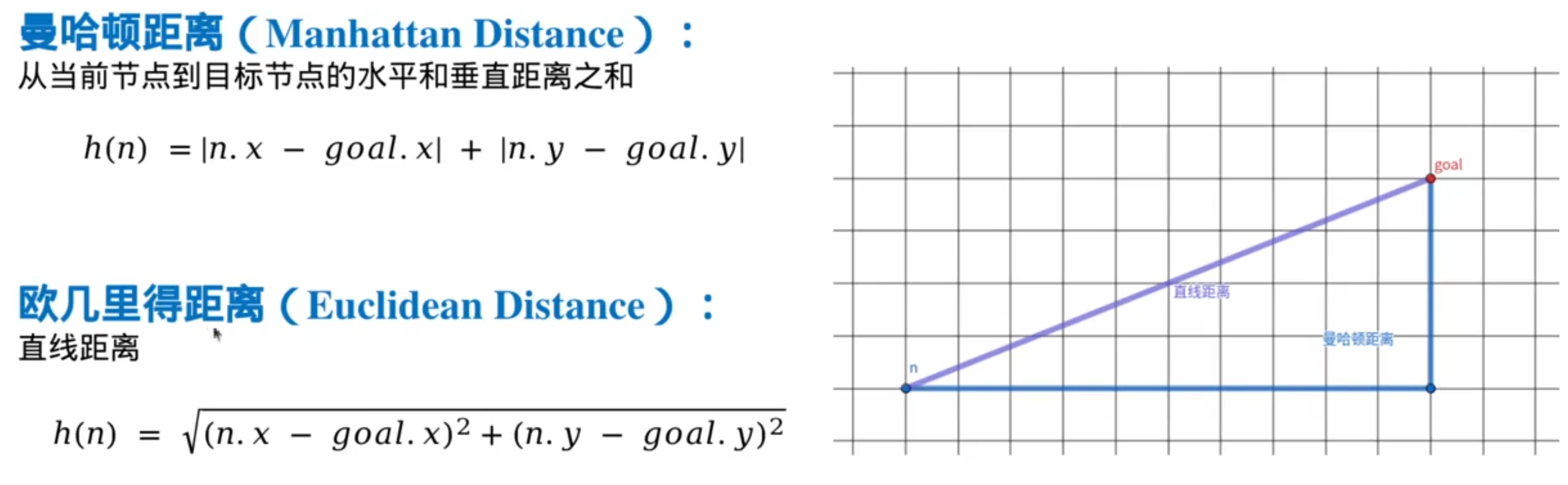
注意:曼哈顿距离>真实距离(有可能无法保证路径最优),但就因为它比较大,所以有时候它的效果最好
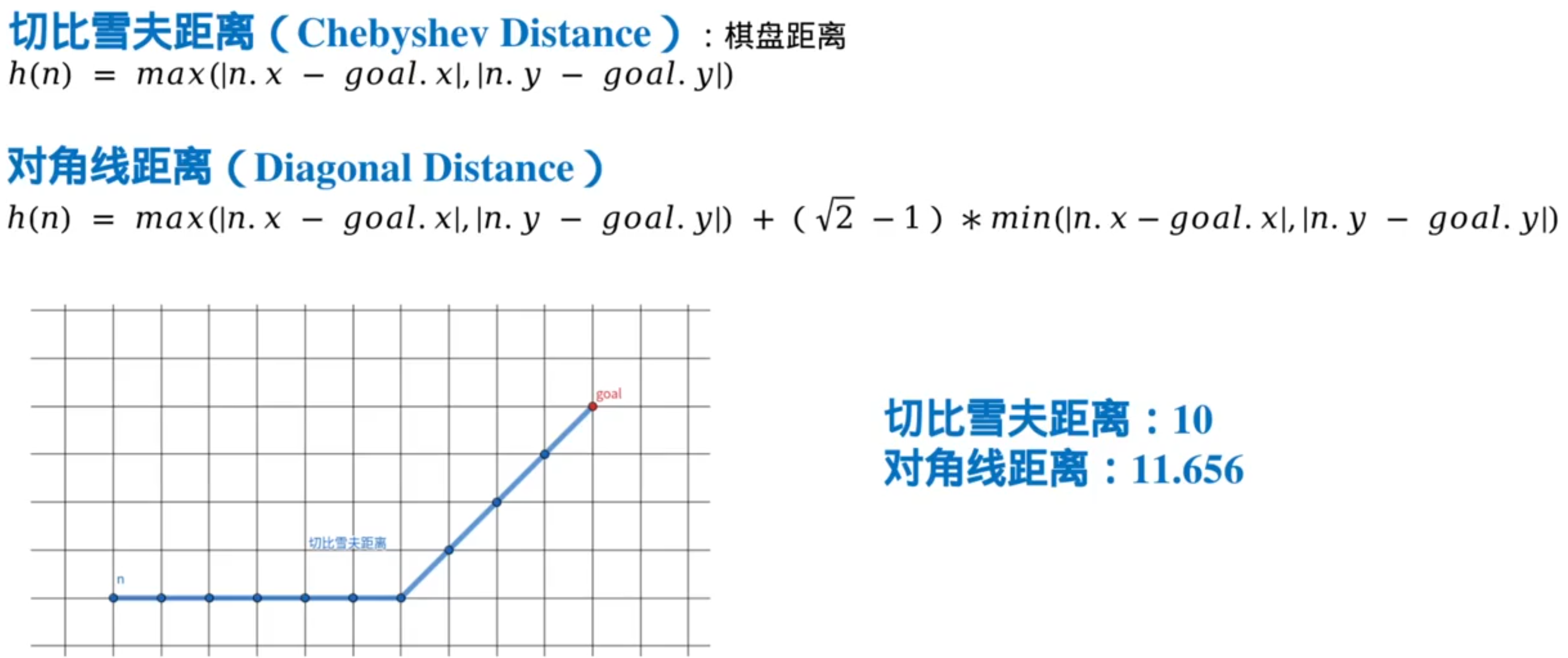

A*算法的最优性保证:
只有满足条件,A*所得的路径才是最短路径
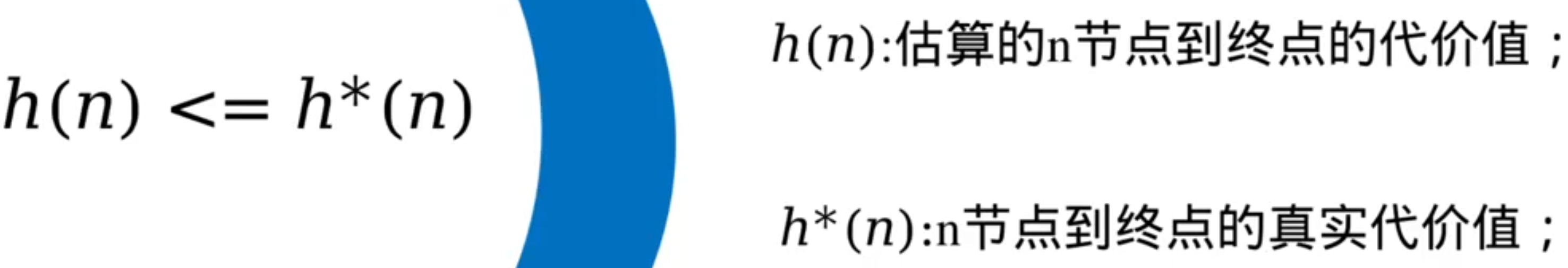
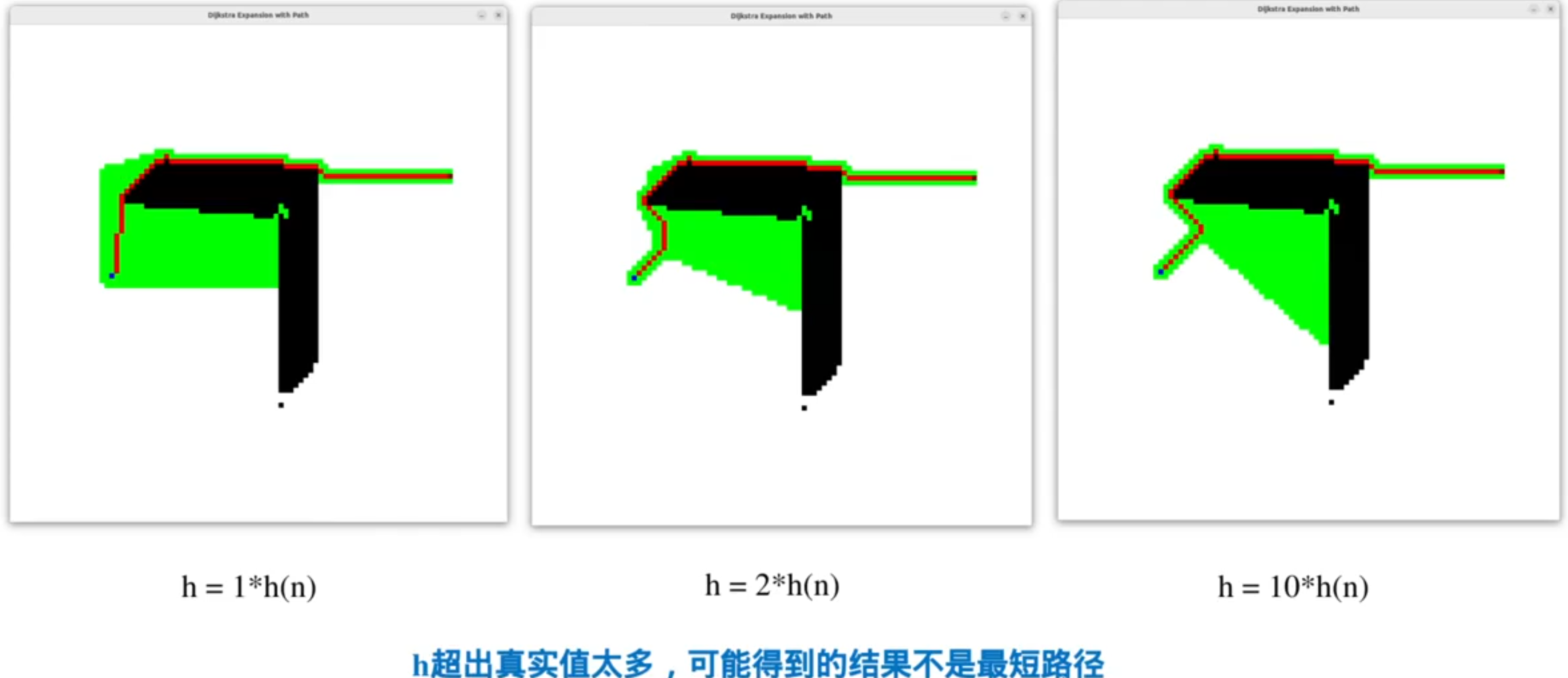
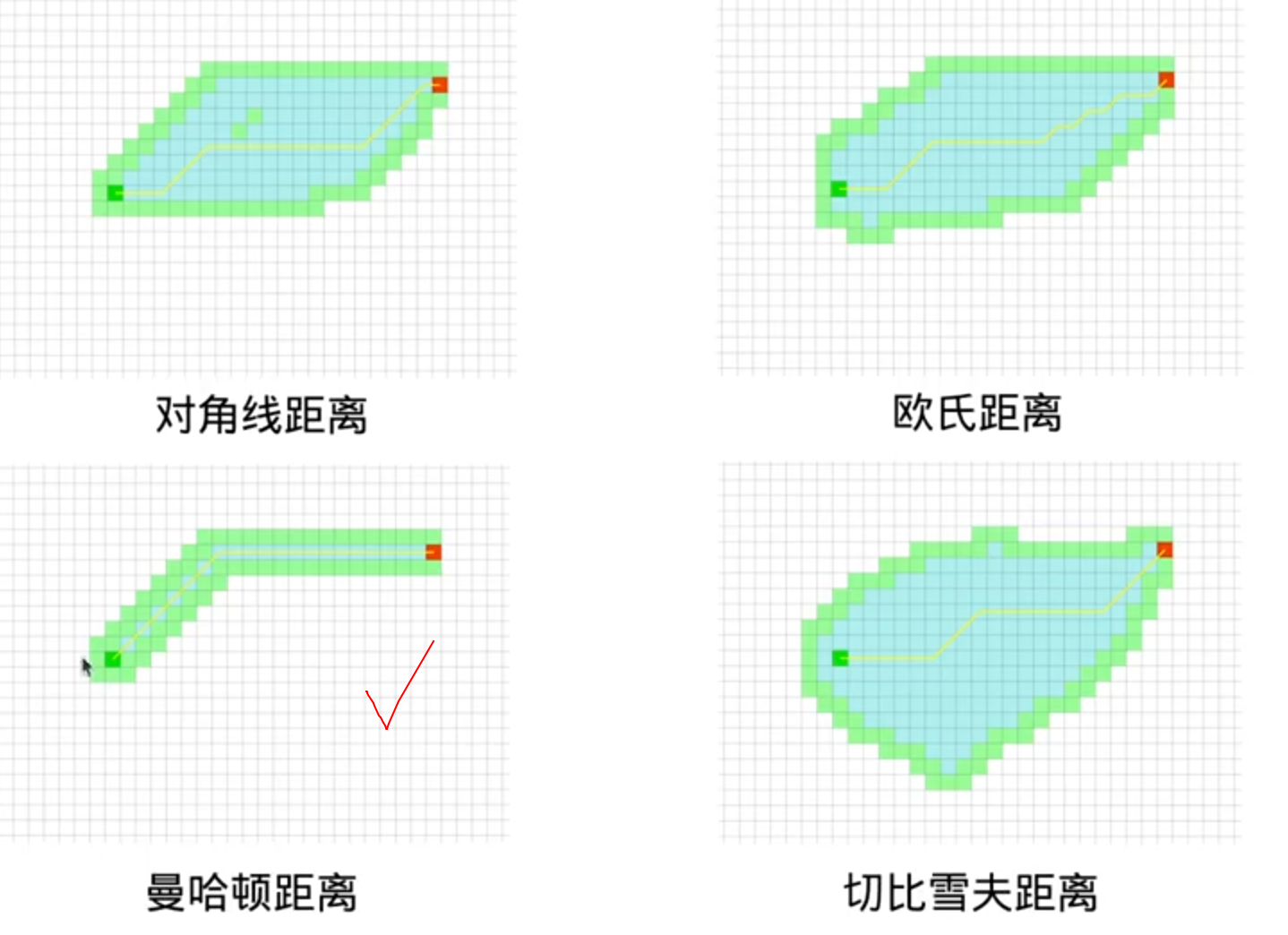
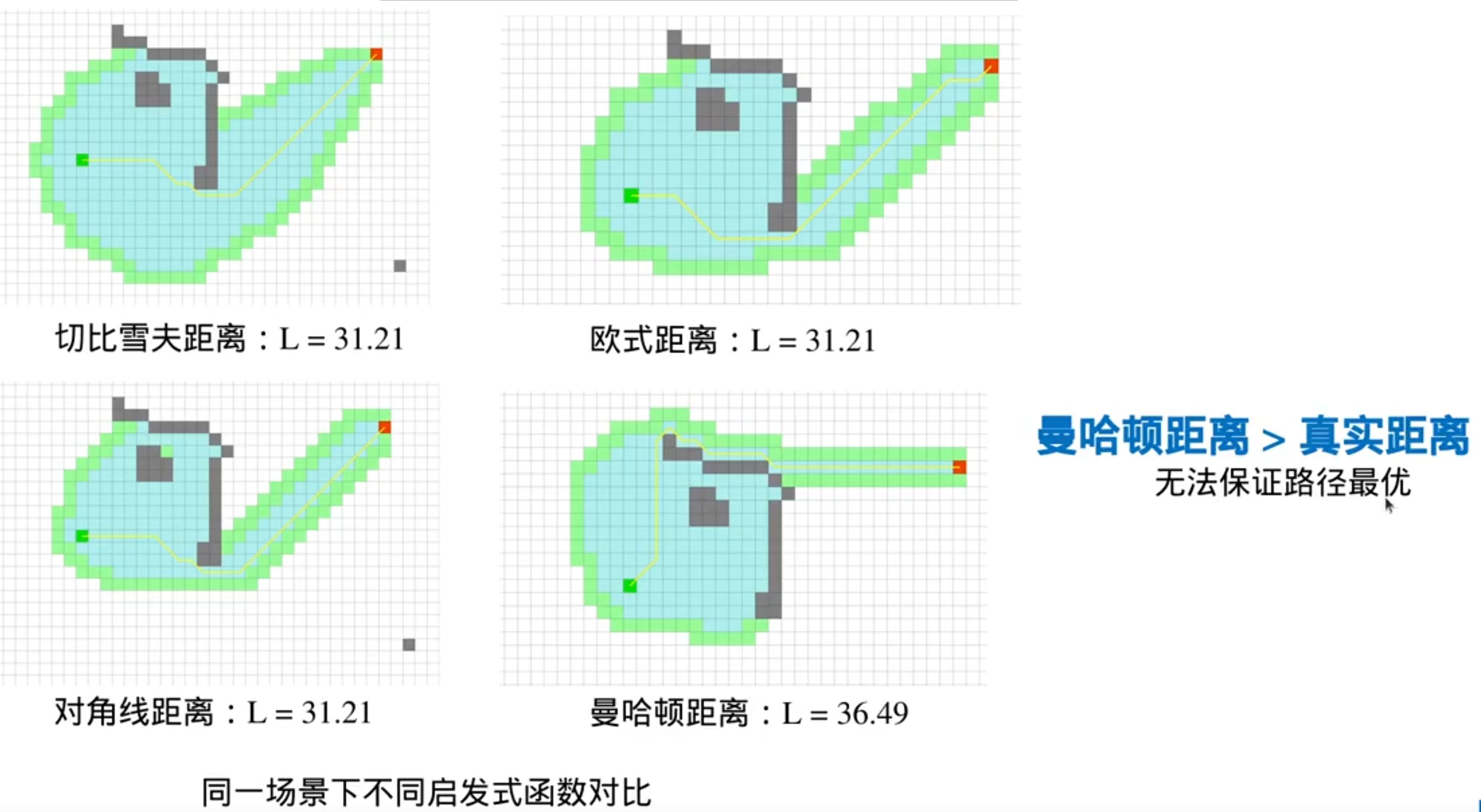
启发函数的选择:

A*的平衡性问题:
虽然A* 算法的结果和理想结果的路径都是最短的,但是理想结果的转折更少,更适合使用,而且A* 算法搜索的节点还是有点多
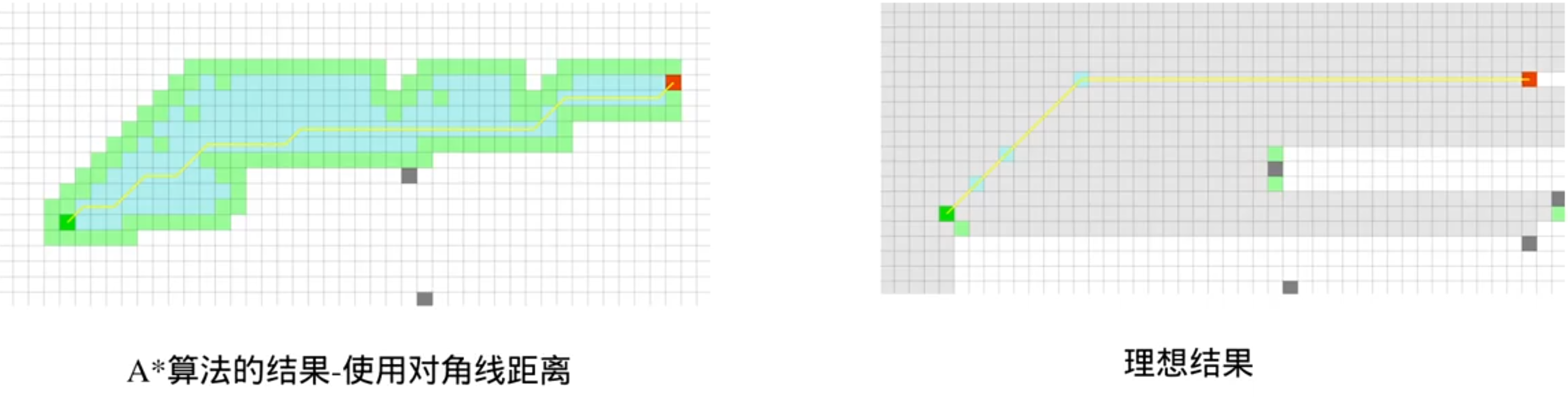
怎么解决呢?
从Dijkstra到A *增加了一个指标,效果大大提升,那再加一个指标

在实际工程上,DFS会用递归方法实现

一种有趣的搜索思路:JPS
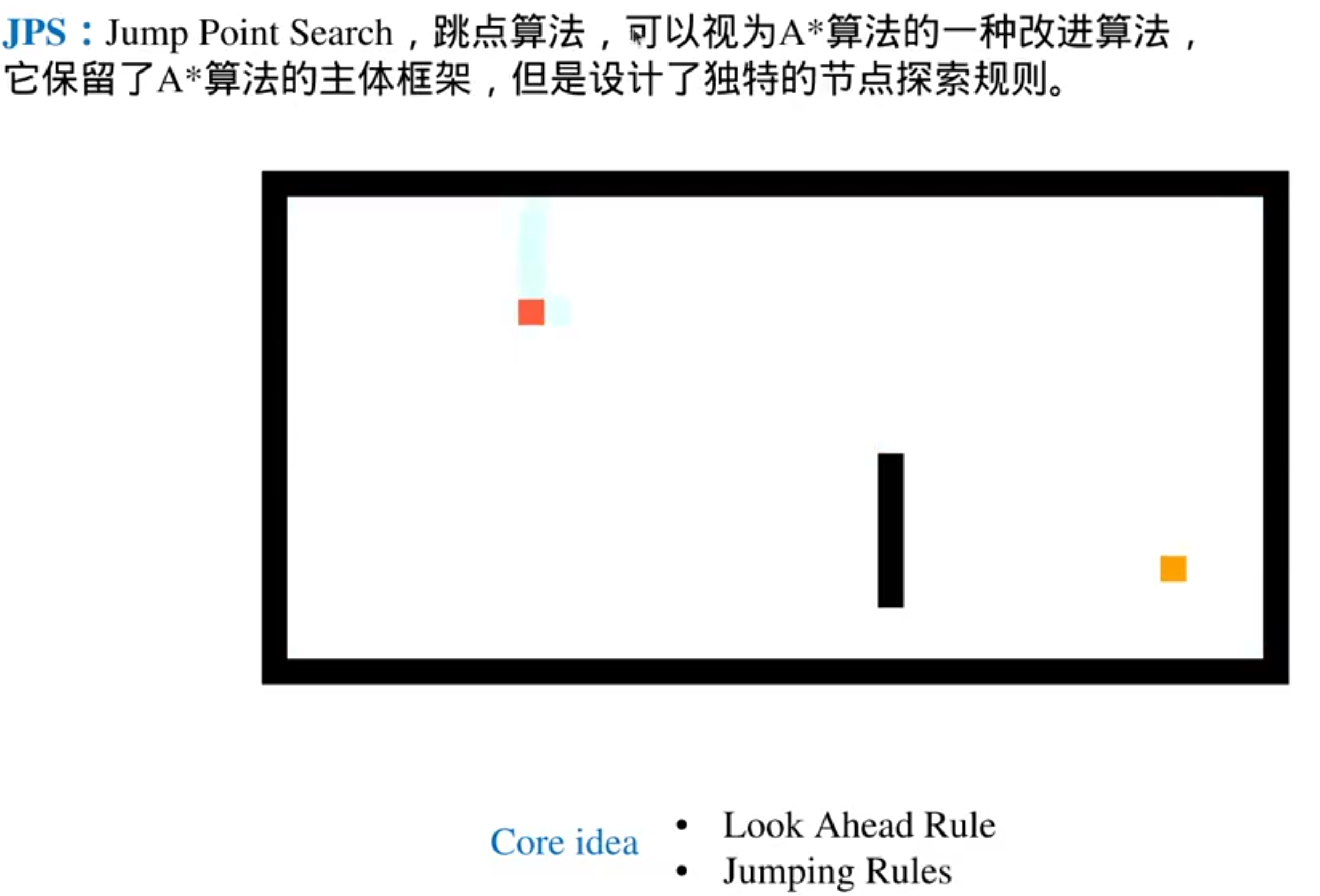
JPS是一种跳跃式搜索算法:关注障碍物边缘的关键性节点(最短路径是起点+障碍物边缘节点+终点)
解决A *算法的平衡性问题
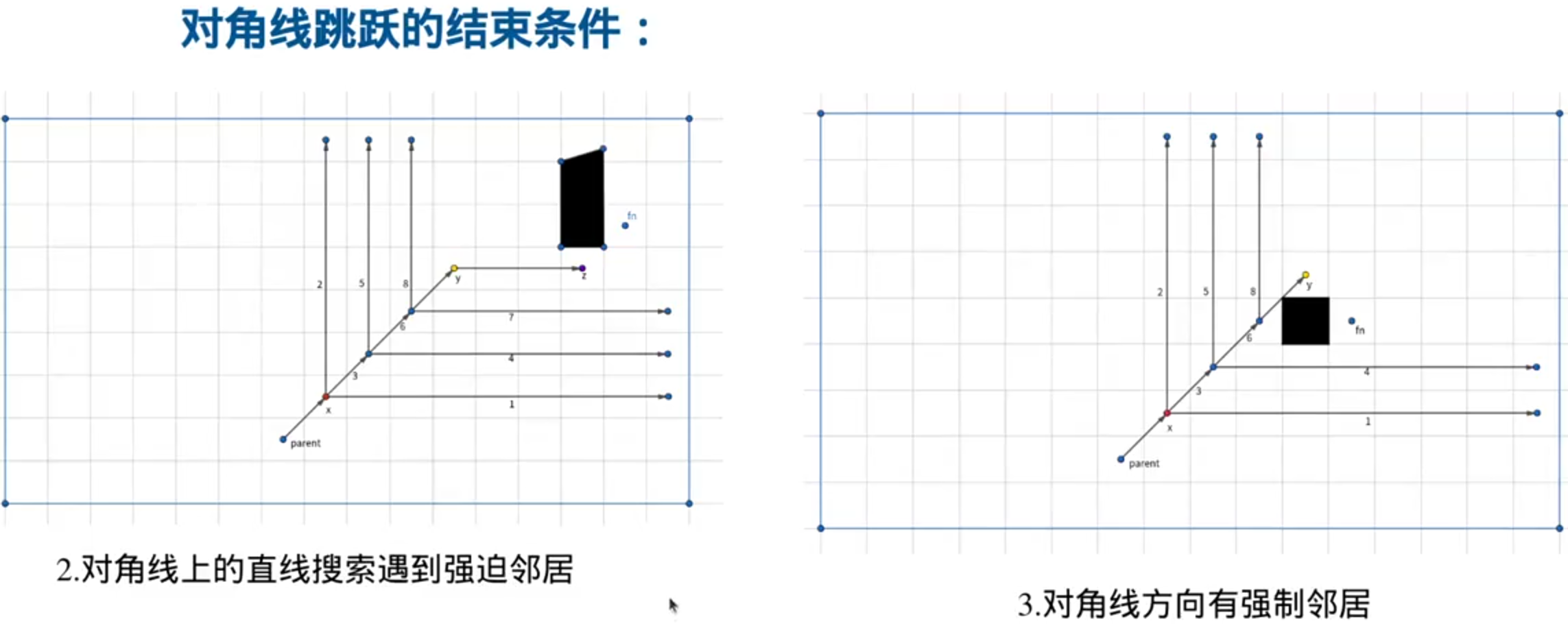
强迫邻居是必须要探索的点(强迫邻居有可能就是绕过障碍物的关键节点)
跳点和强迫邻居都需要继续拓展,所以都要加到openlist里面
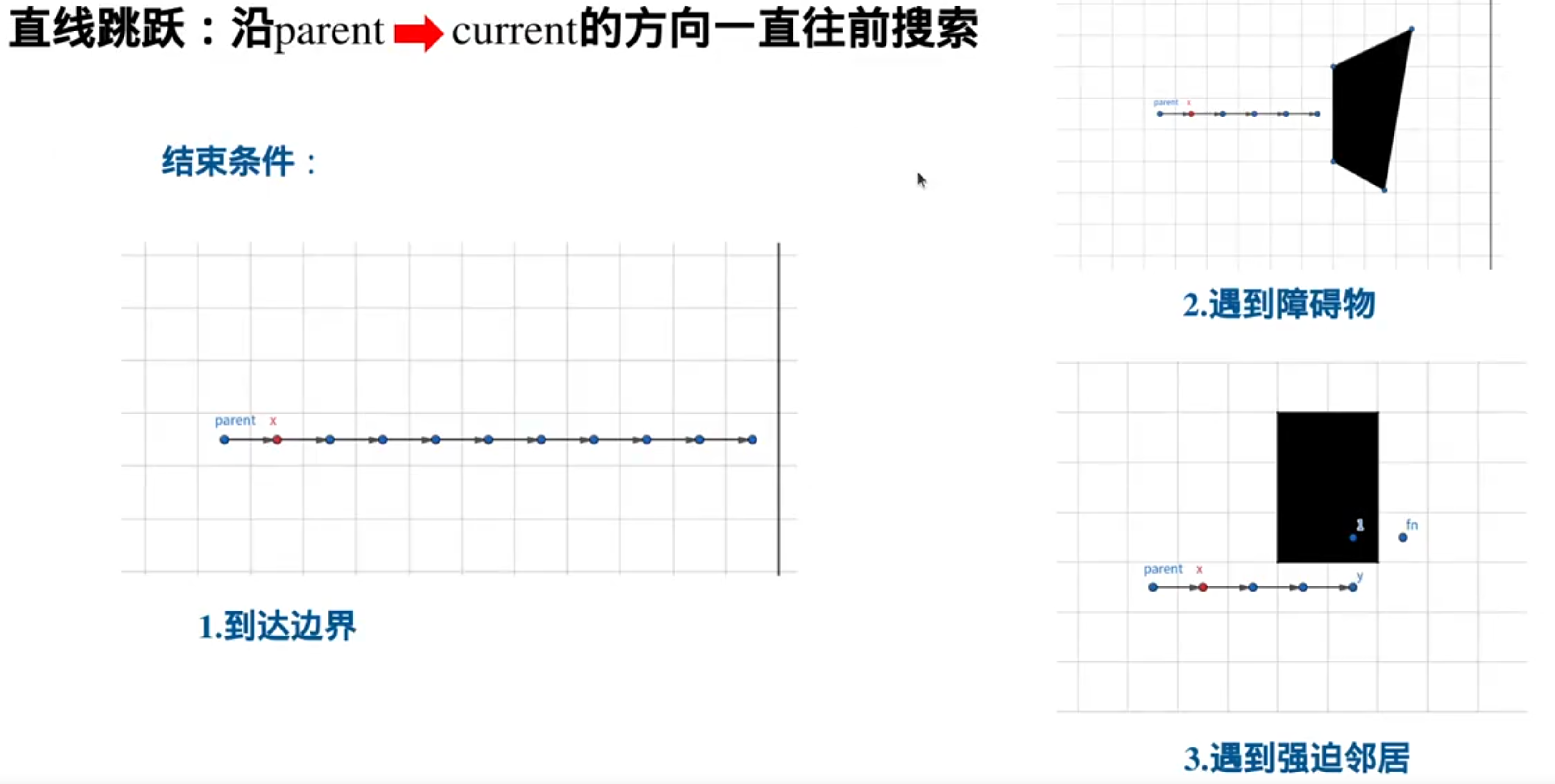
这就是向前看规则:
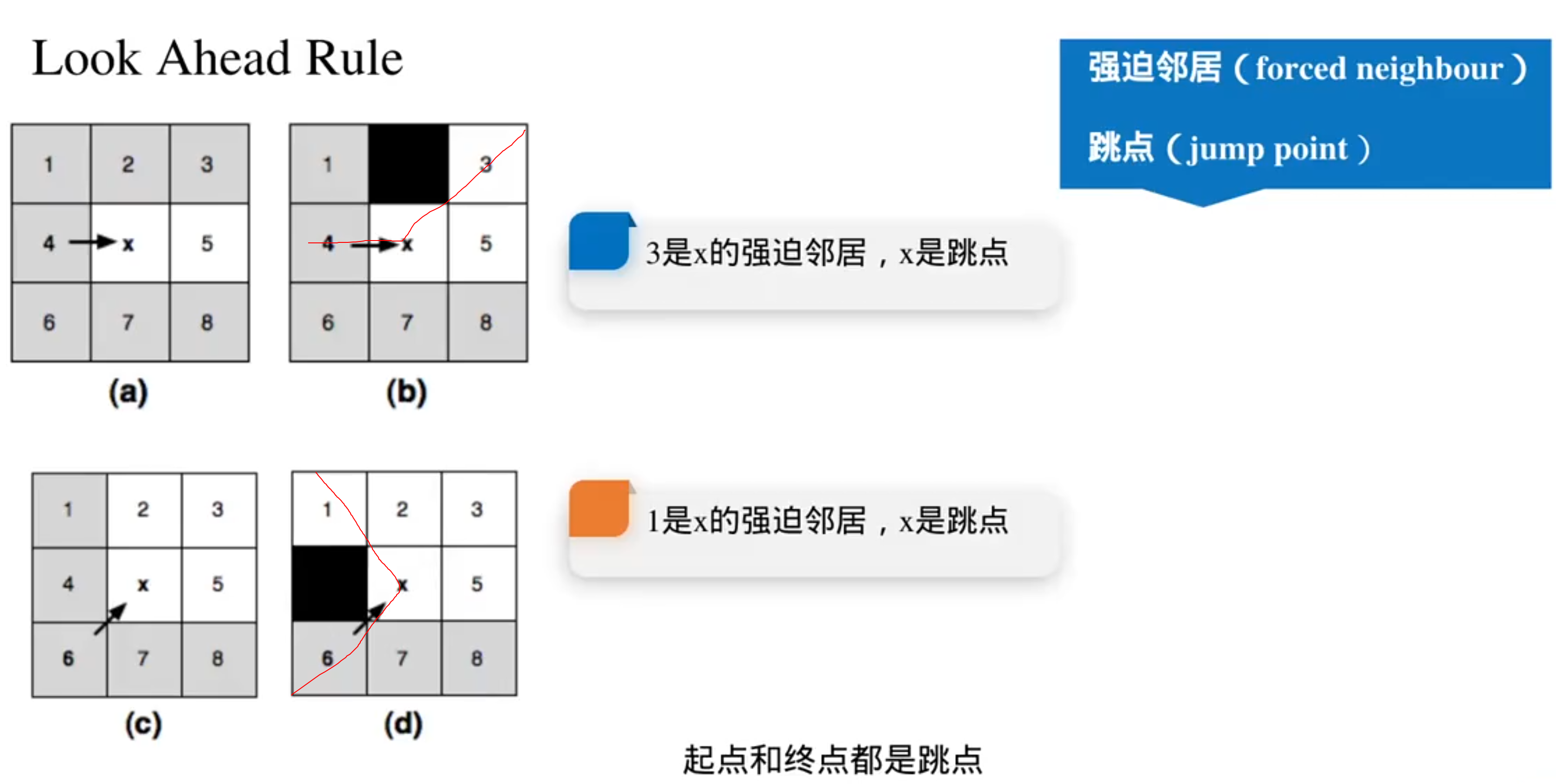
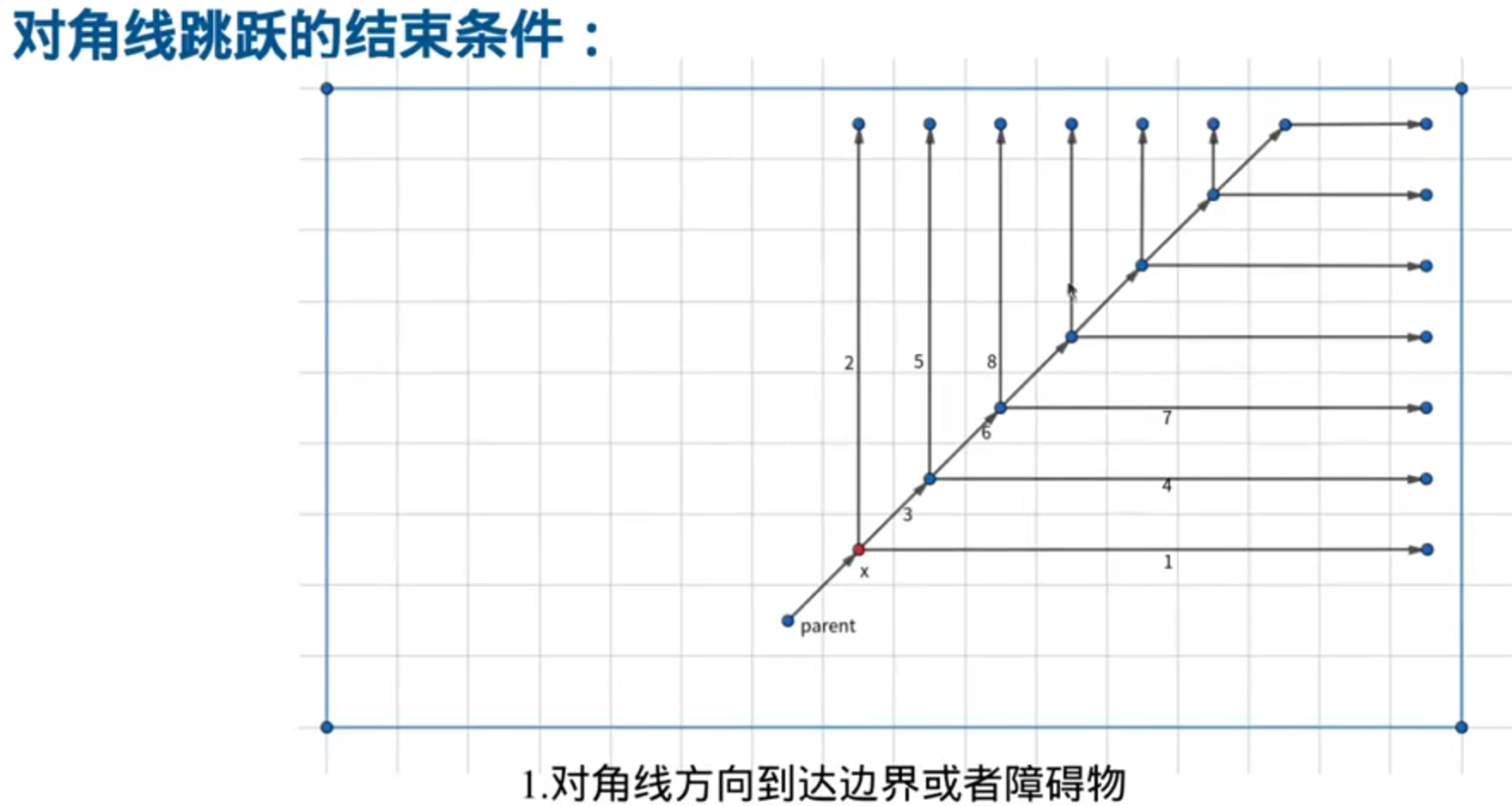
跳跃规则:
起点的八个邻居都需要加入到openlist里,都需要拓展

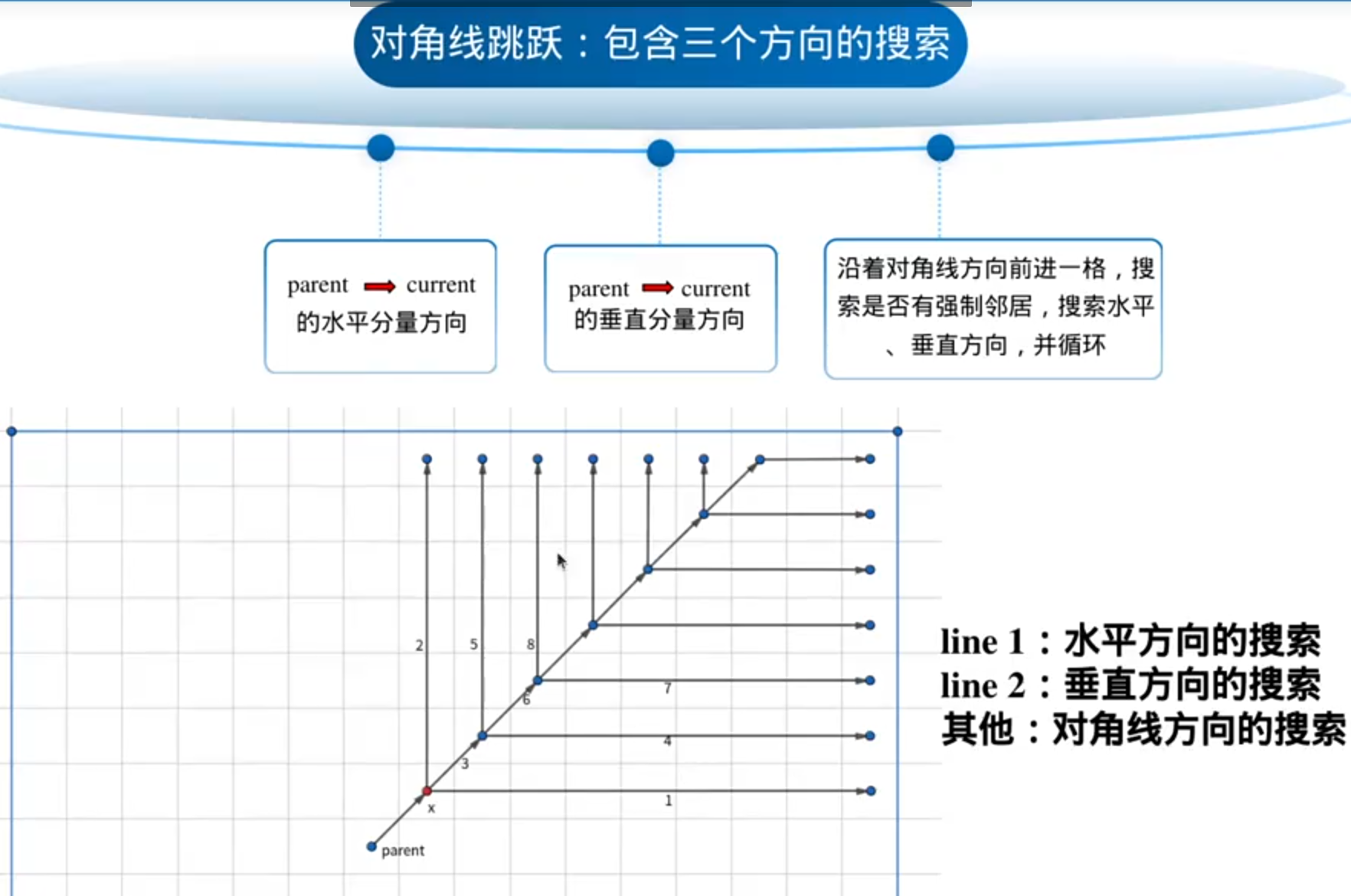
八邻域探索方向可分为正向和对角线方向

A*会八个方向一圈一圈的探索,JPS是只沿一个方向探索:

对比:
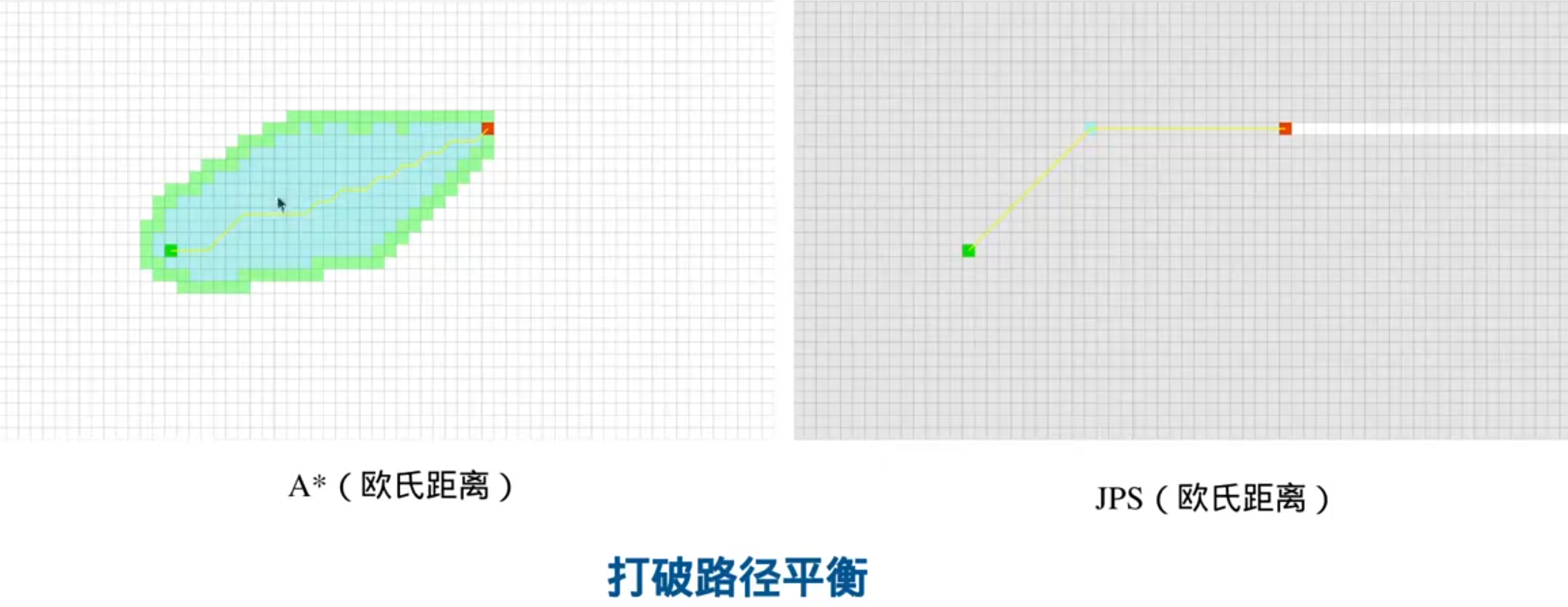
蓝色是被拓展过并添加到openlist里的,绿色是没有拓展过但是添加到openlist里的,右图里灰色是访问过的点
A*的openlist里的节点更多

从容应对动态障碍物–D*(动态A星算法)
D* 又称Dynamic A*
初始生成一条最优路径,在跟踪过程中,根据障碍物的变化,实时调整受影响的局部局部路径
算法流程:

1.方向构建:
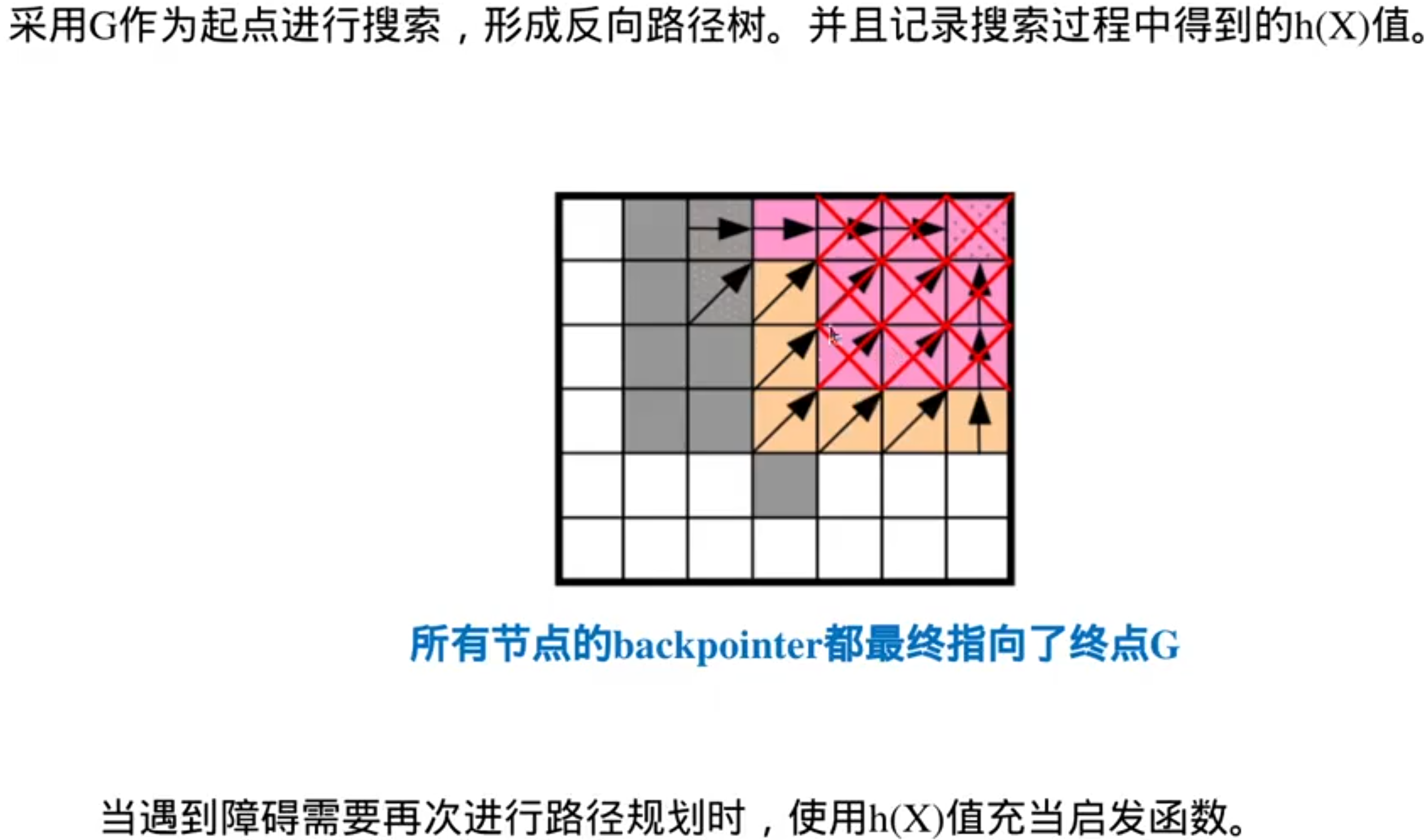
h(X):用来存储路径代价,指从X到达终点G的路径({X,……G},简记为{X})代价,不一定是全局最优,第一次搜索到起点时时,所有点的h会被更新,计算方式同Dijkstra算法,是用相邻两点的代价+上一个点的代价累加得到
k(X):用来记录自X节点被加入到OPEN_LIST中后的最小h(X)值(具体计算方式由Insert函数决定),也是优先队列OPEN_LIST的排序依据,k将会保持到最小,它表示了本点在全图环境中到G点的最小代价(k(x)没有受到障碍物增加的影响)
3,代价修改:

4,状态处理



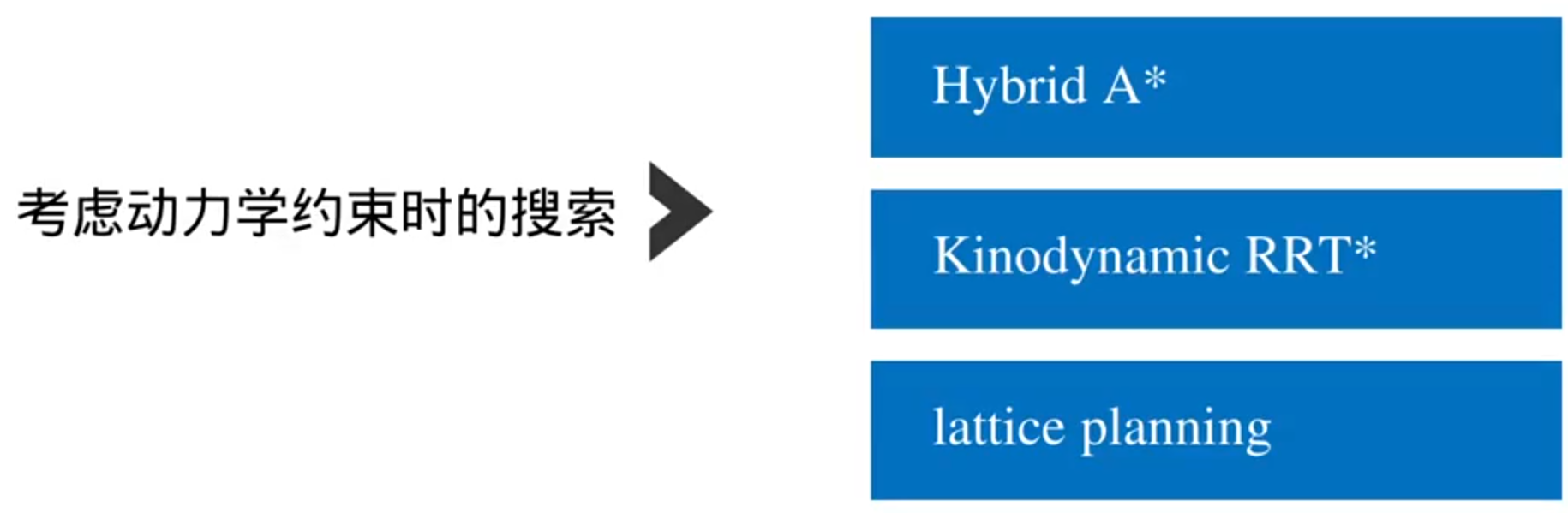
考虑动力学和运动学的路径搜索
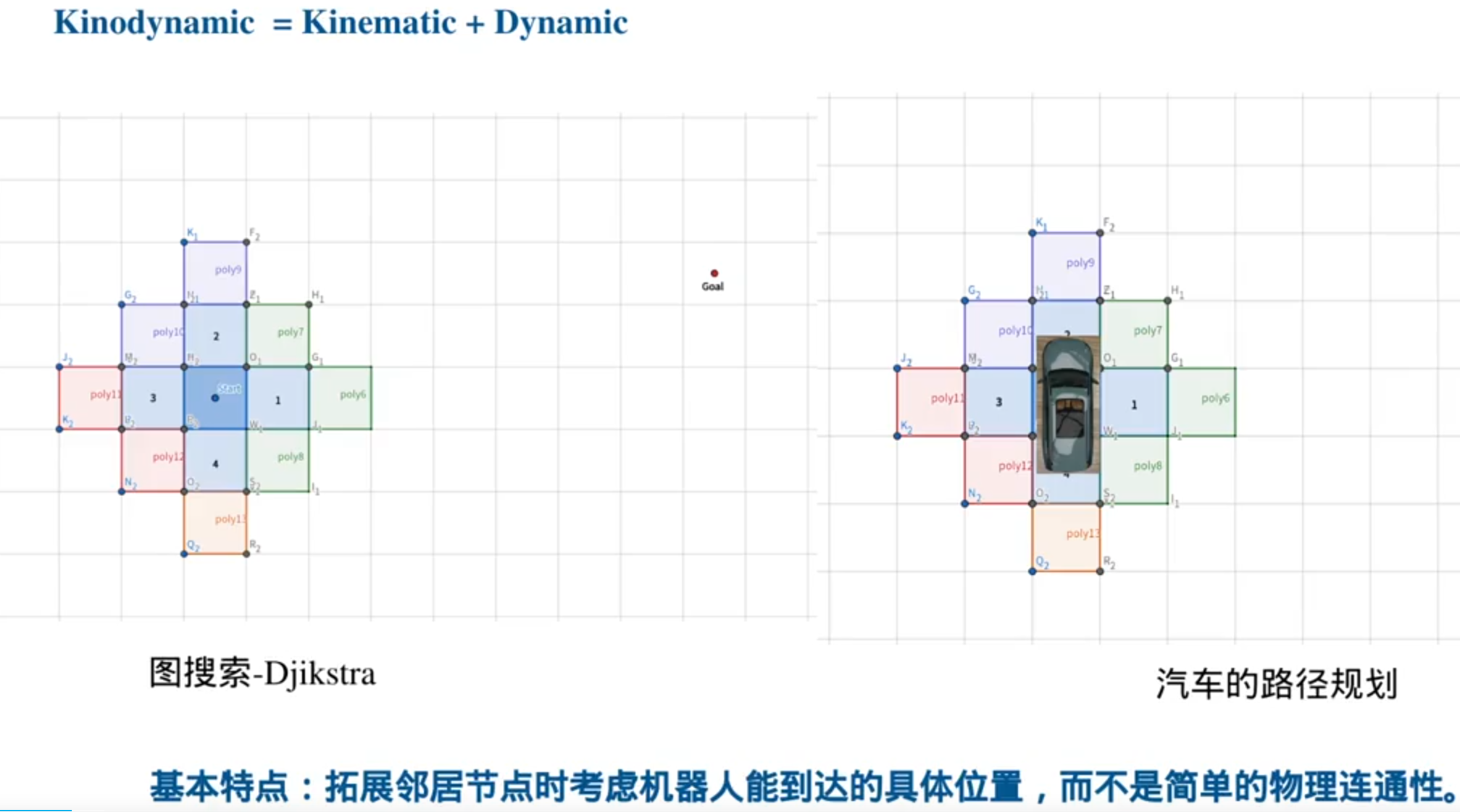
优化了节点的扩展方式,节点不一定是栅格的中心(弧形路径)
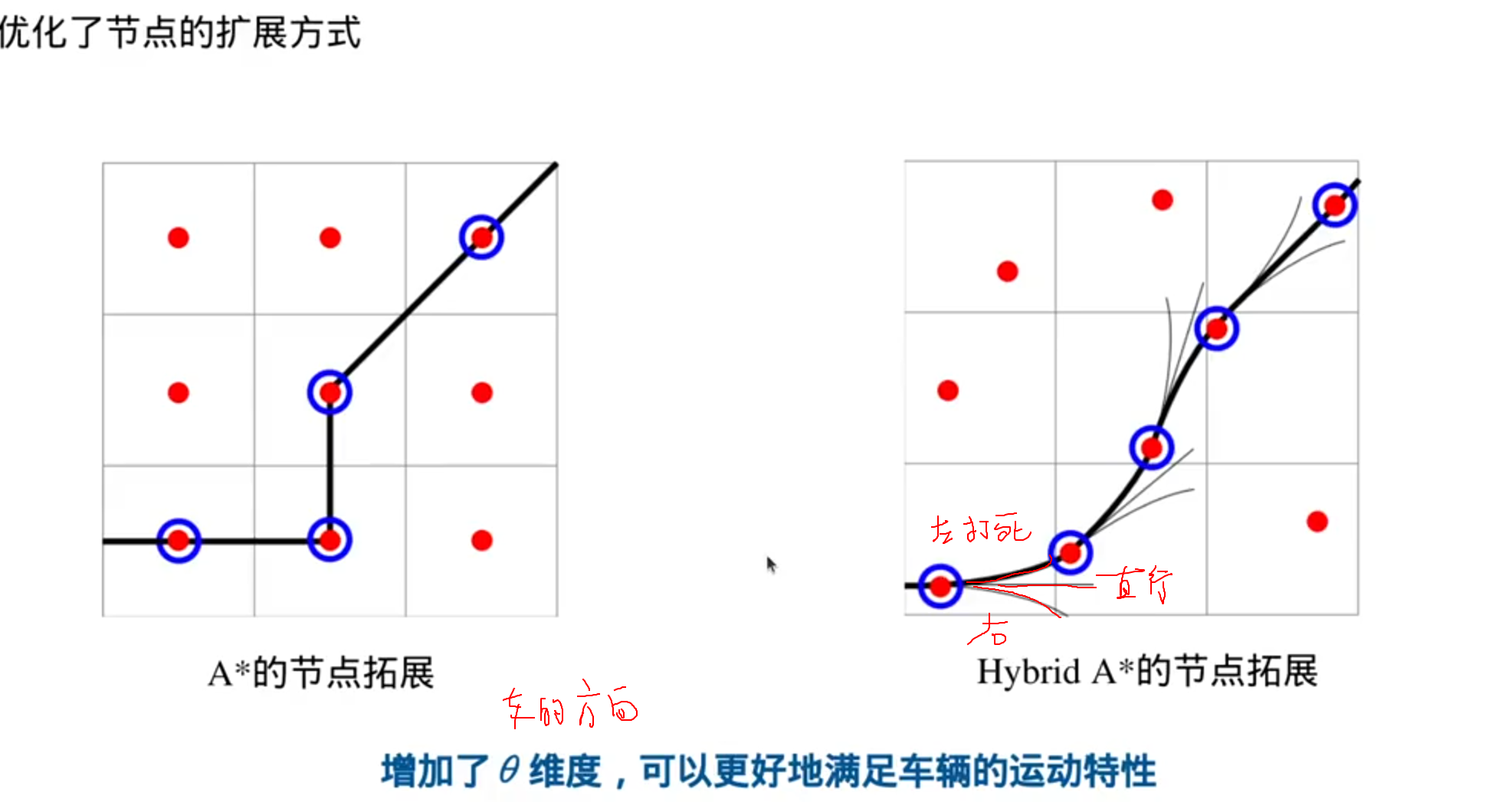
优化了启发式函数
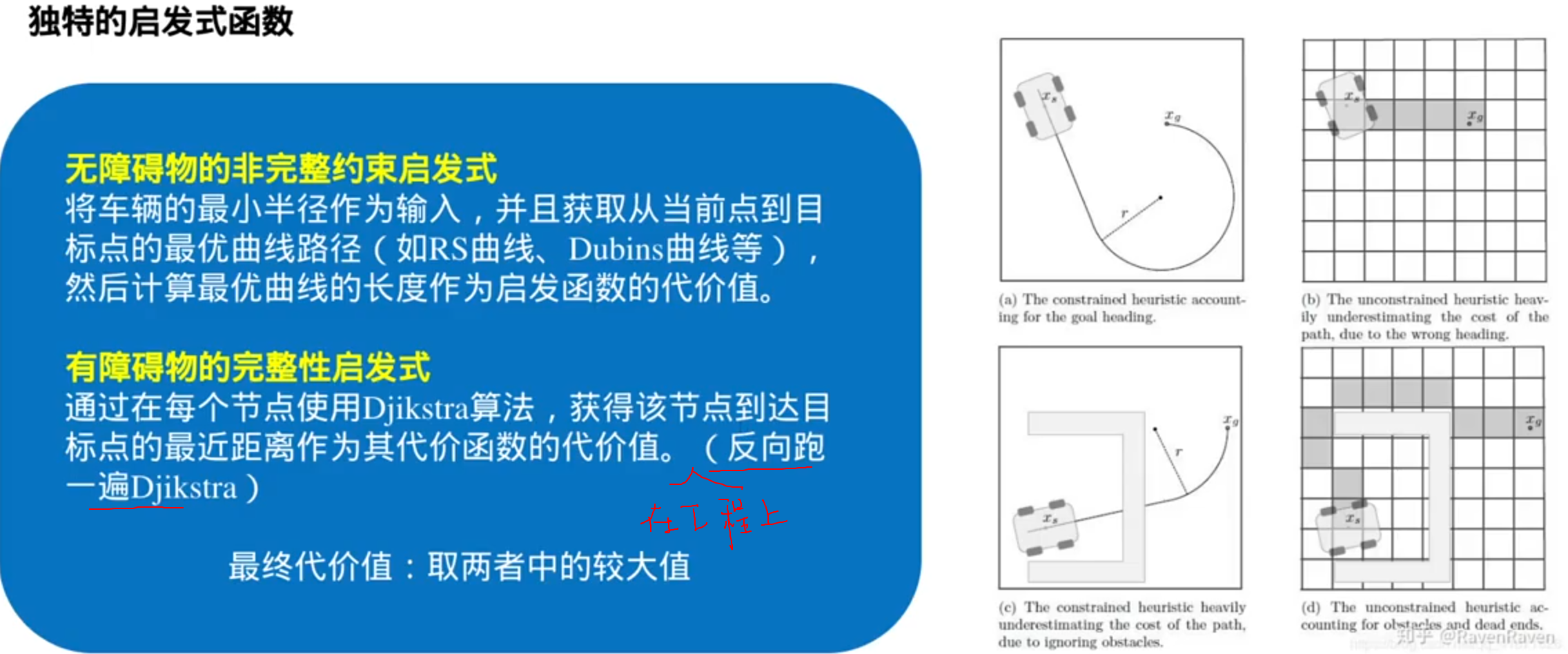
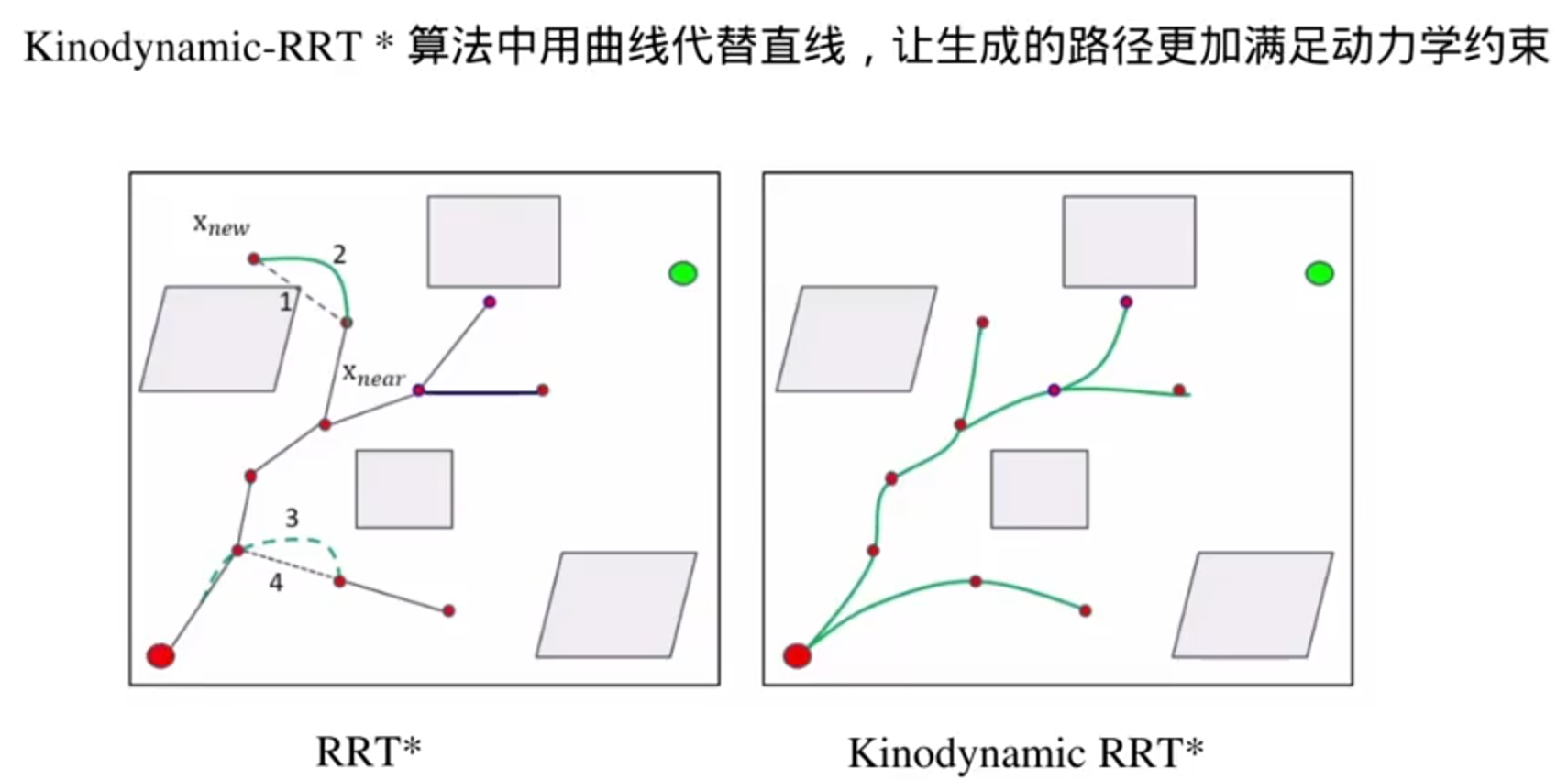
搜索到的路径还要进行轨迹优化
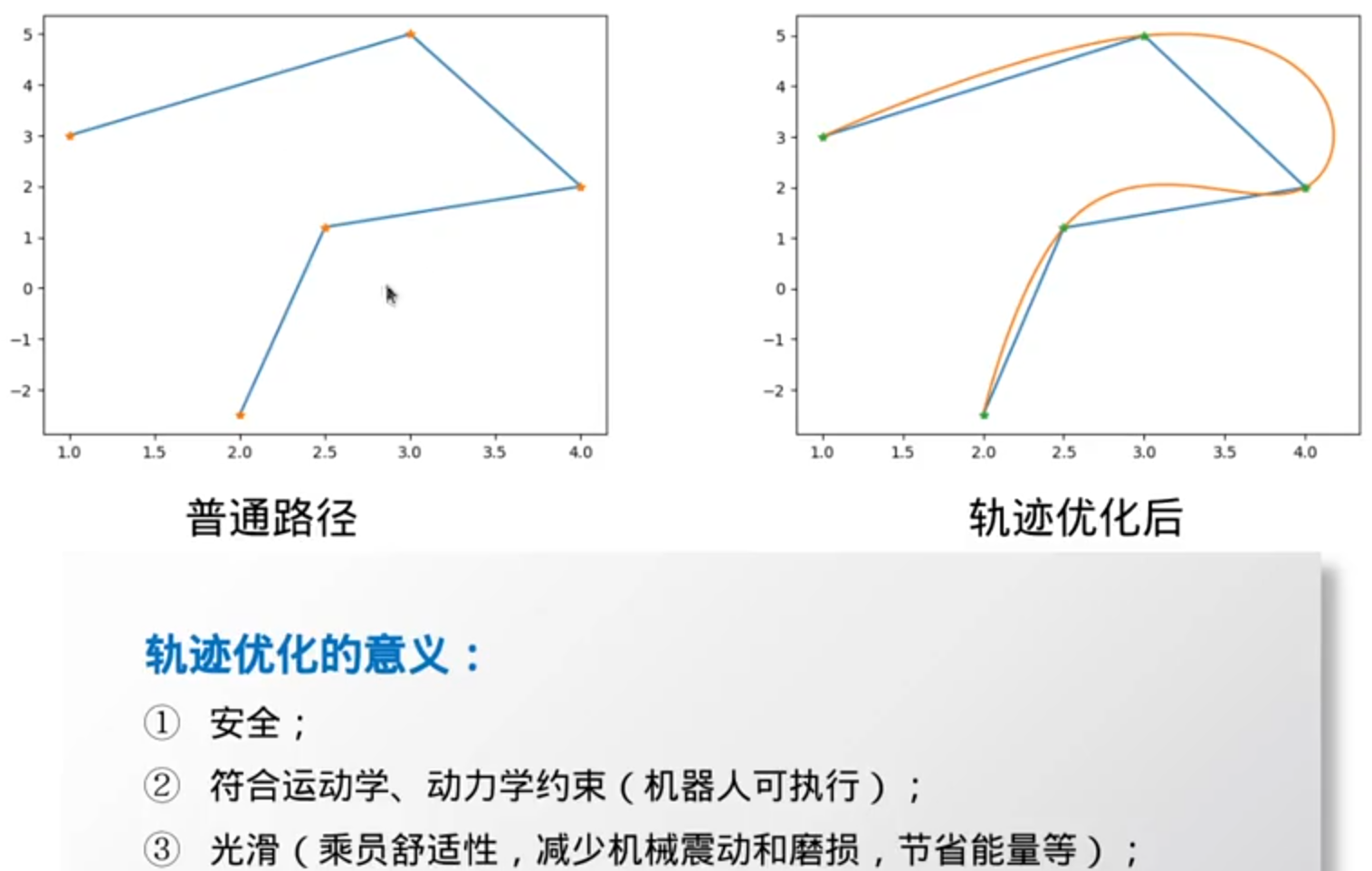
轨迹优化——Min-Jerk(jerk是加加速度)


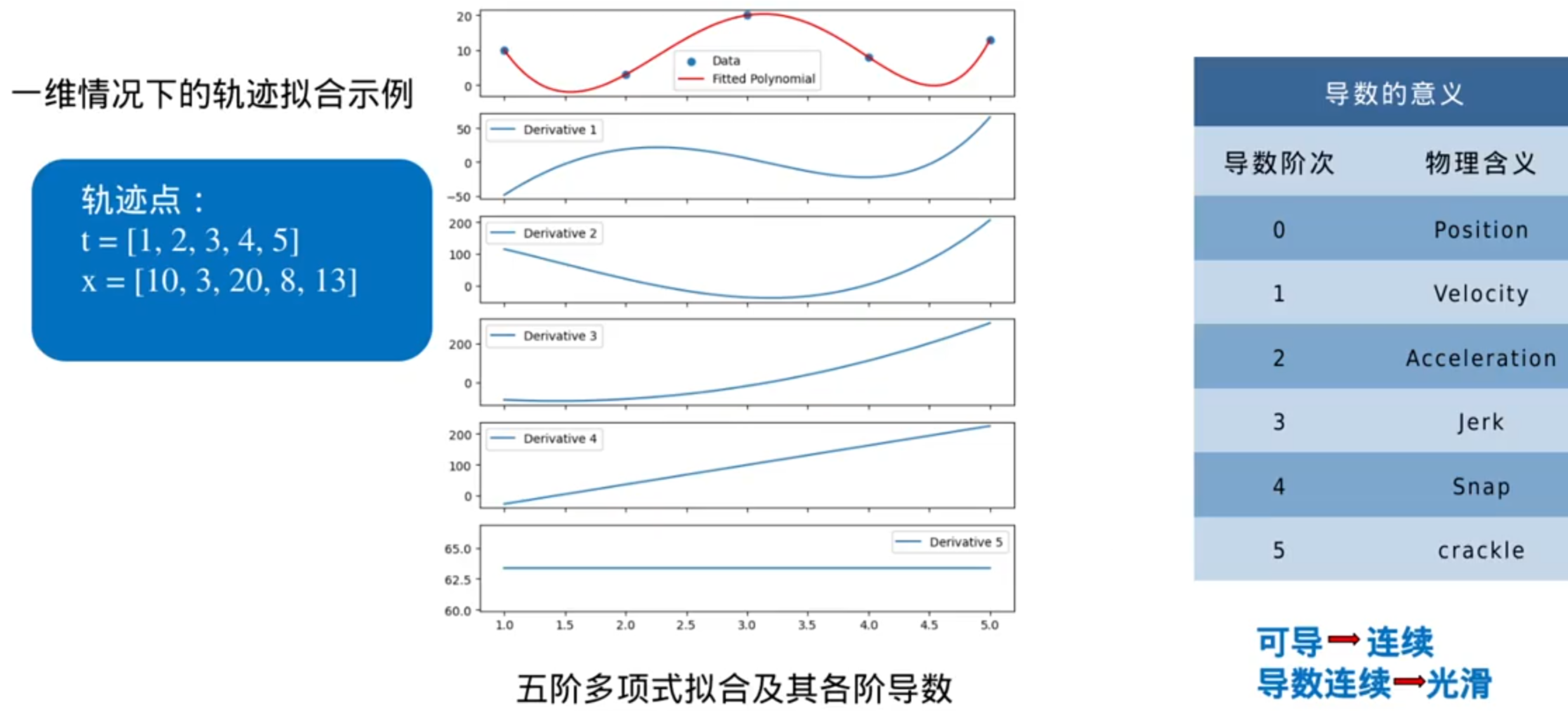
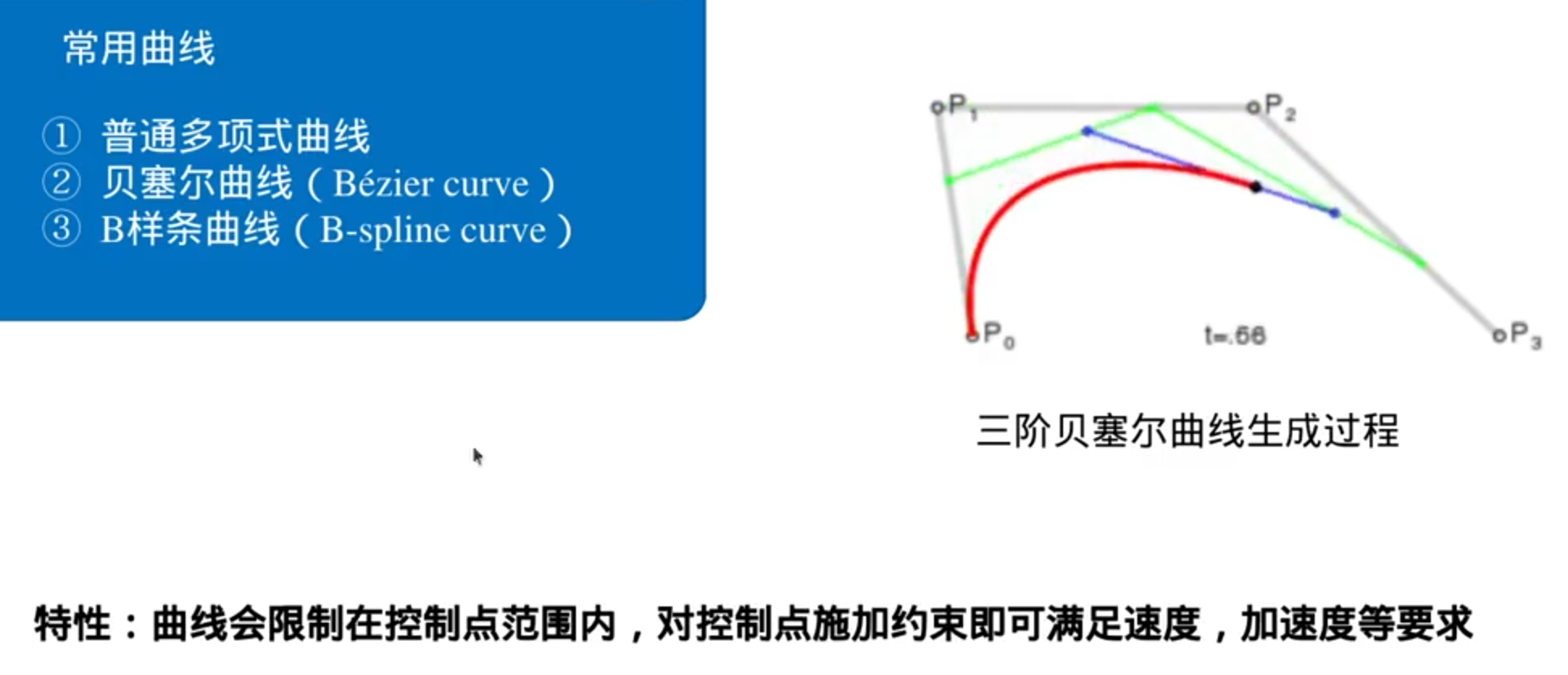
贝塞尔曲线把对连续曲线的规划,转变为对控制点的规划
贝塞尔曲线还有一个巨大的优点:导数还是贝塞尔曲线,仍然有控制点
缺点:贝塞尔曲线的形状完全依赖于控制点的数量和位置
移动一个控制点可能会对曲线的整体形状产生意想不到的影响,这使得局部控制变得困难
B样条曲线解决这两个问题
2.

 Min-Jerk是舒适性,Min-Snap是节省燃料
Min-Jerk是舒适性,Min-Snap是节省燃料
lattice planner
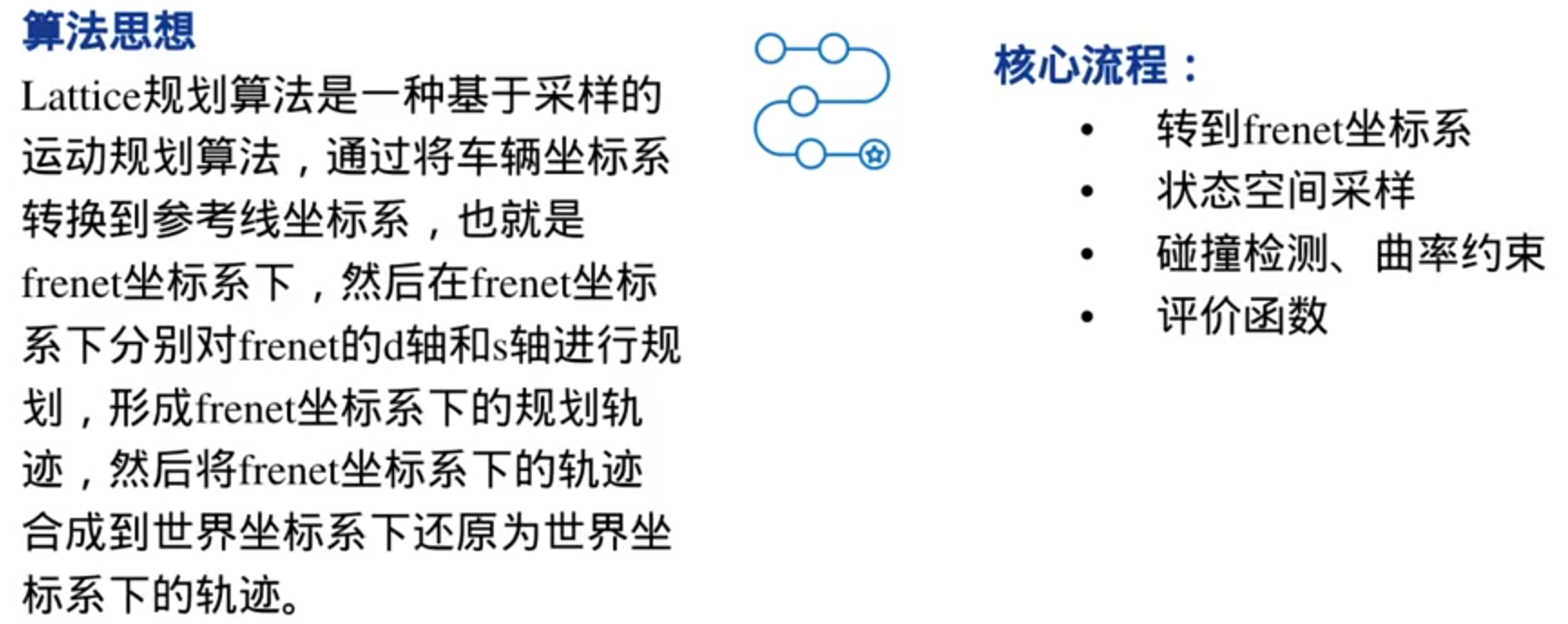
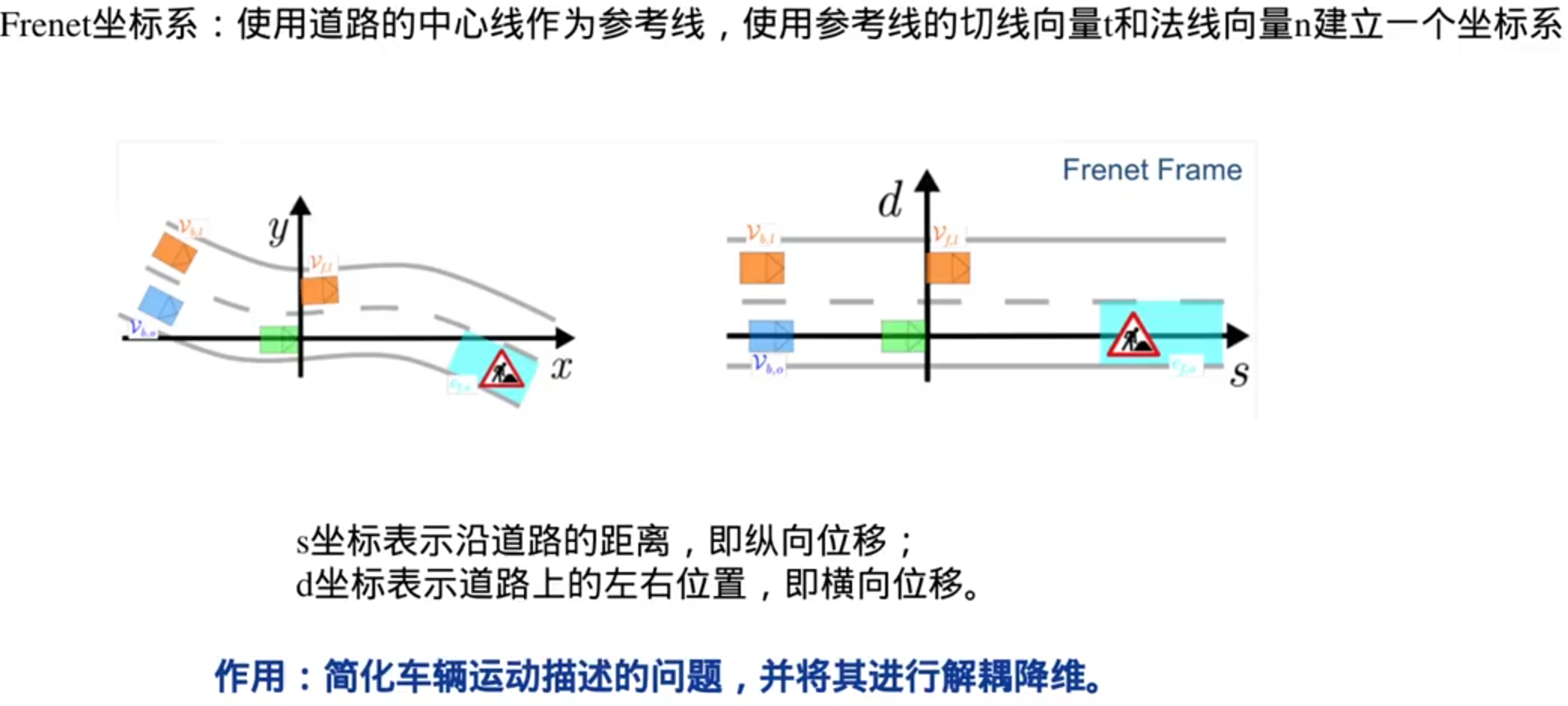
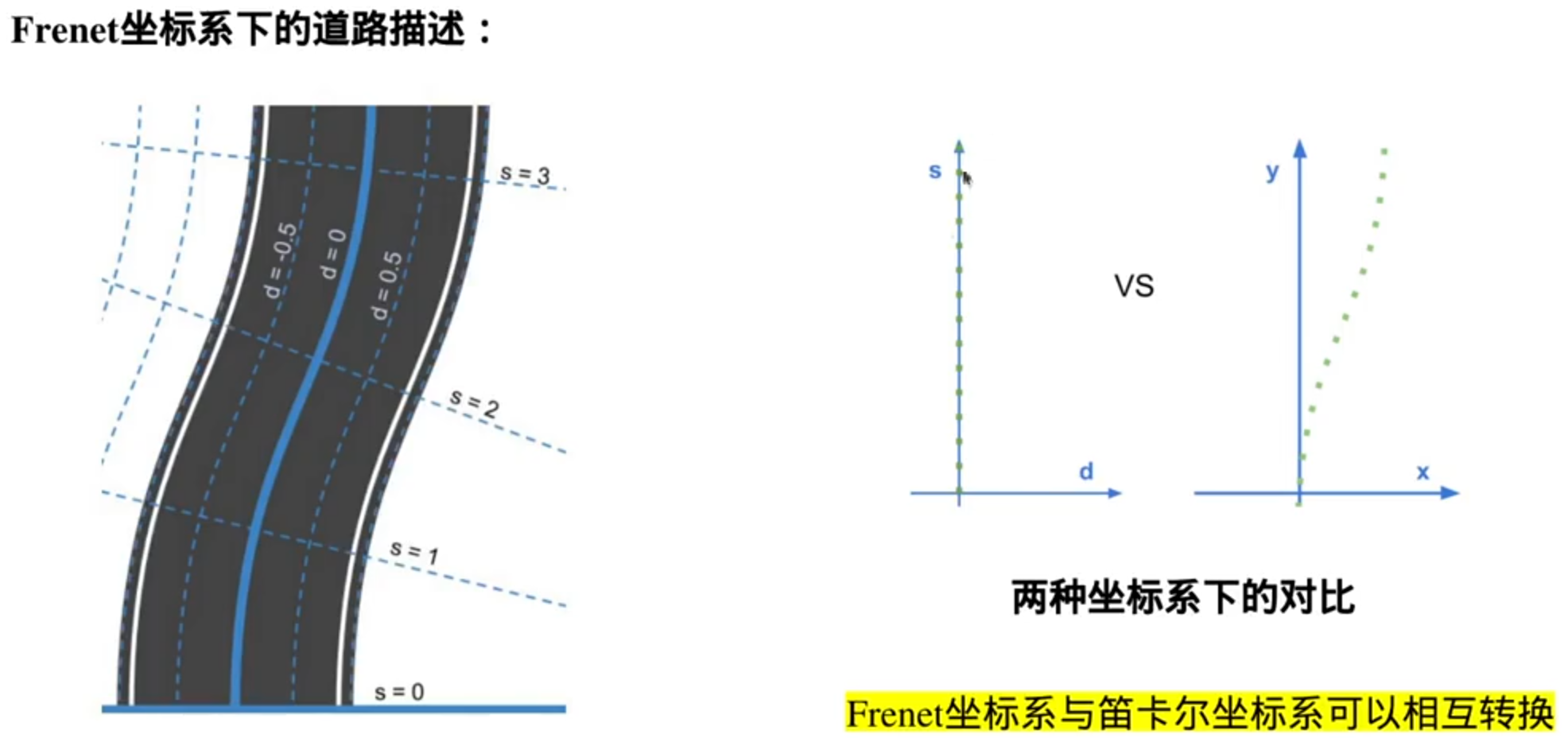
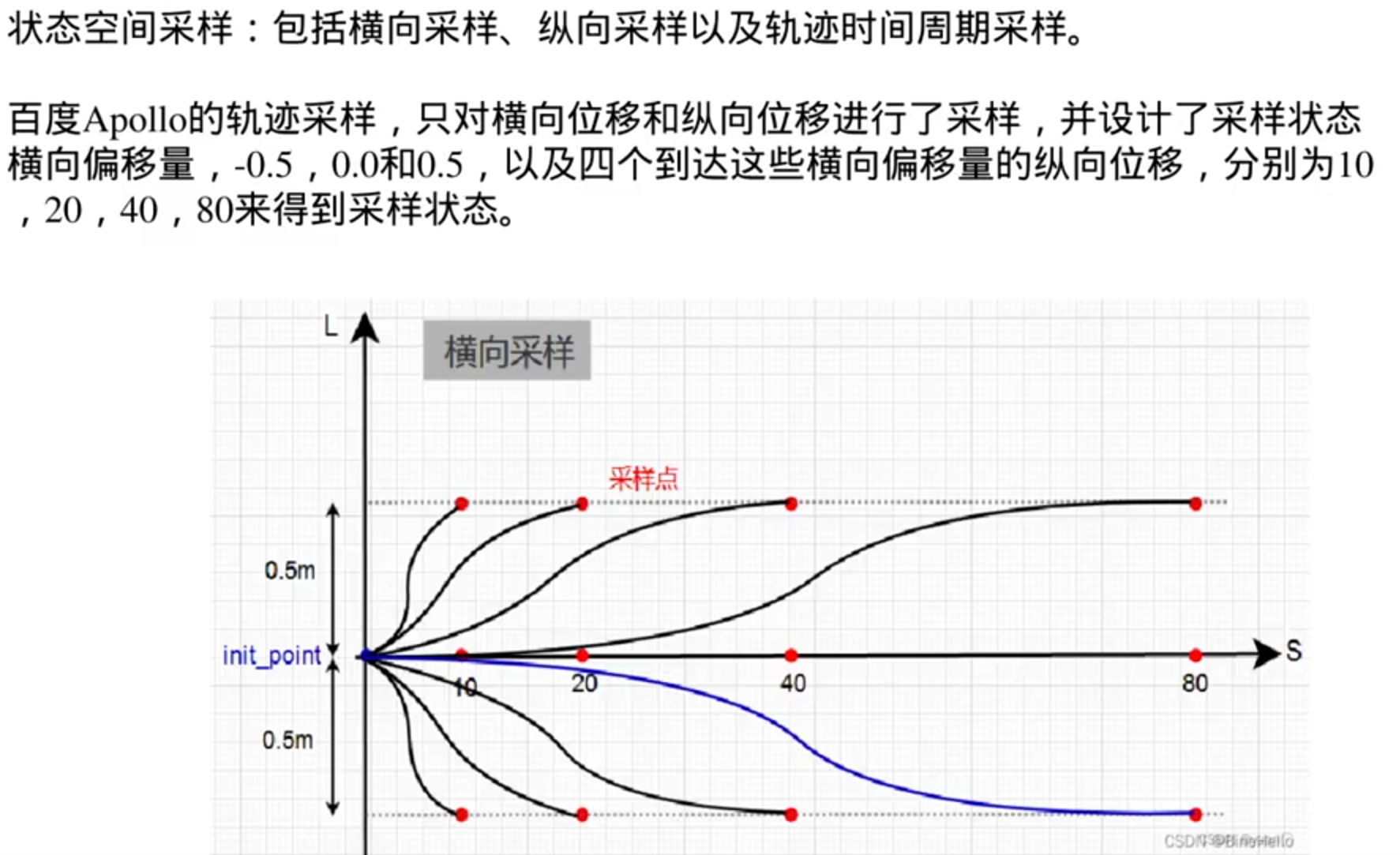
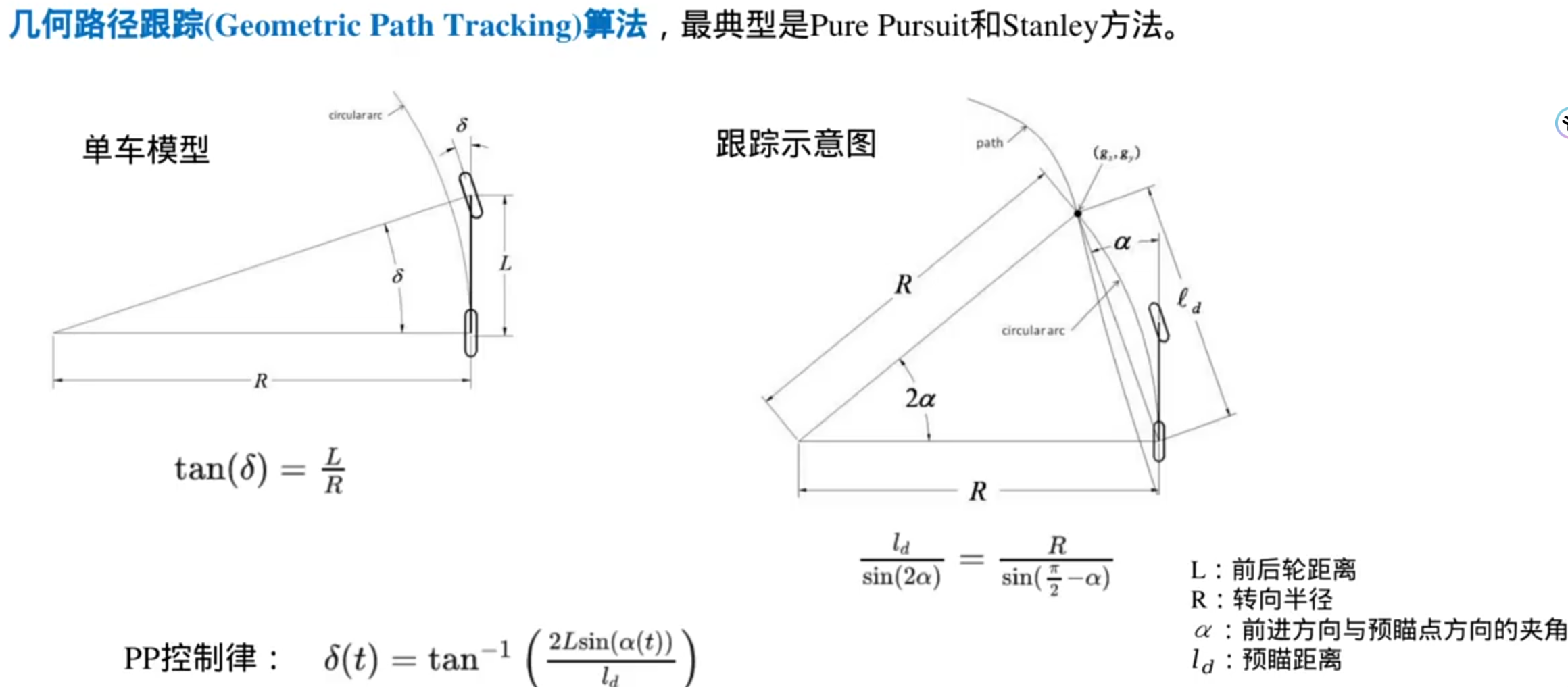
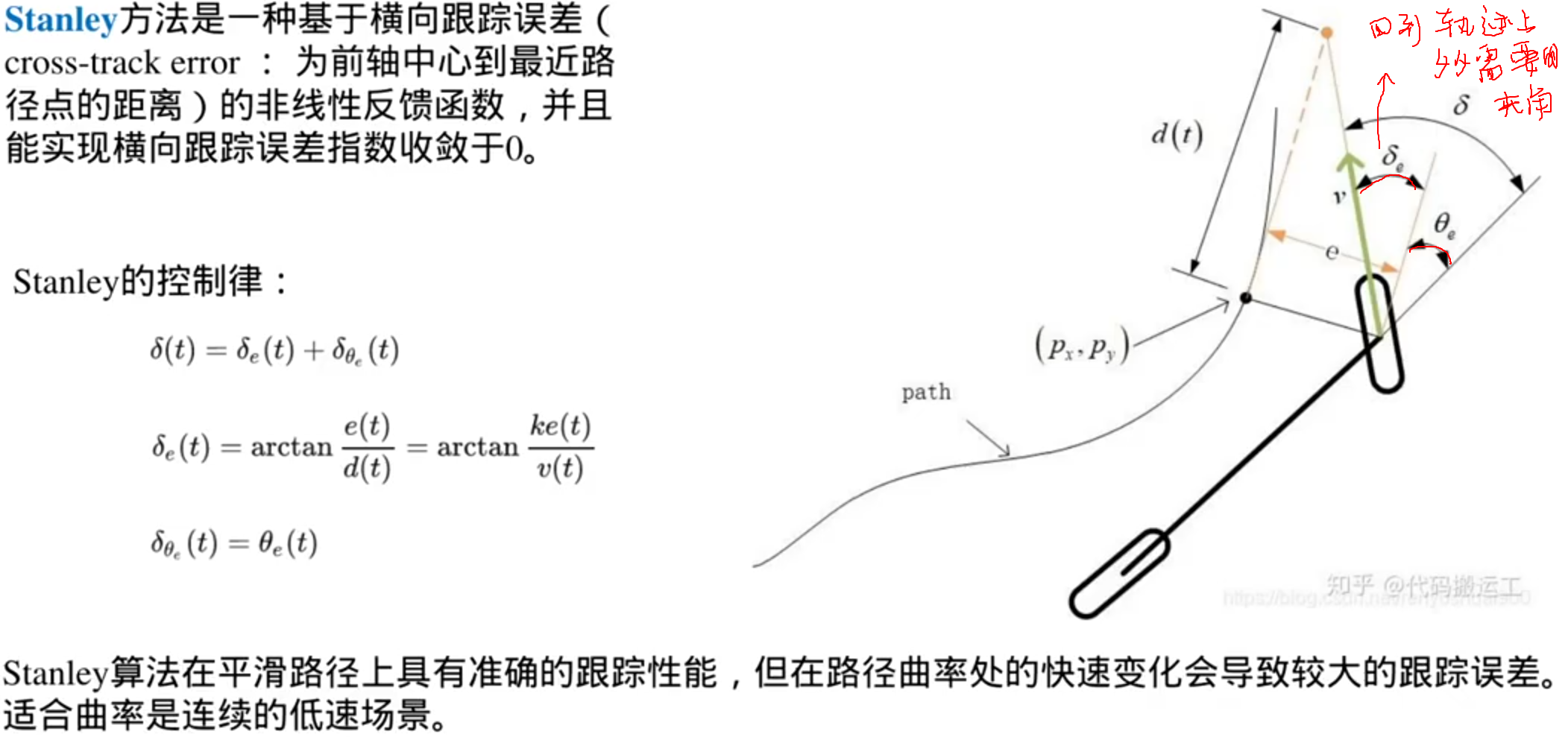
轨迹跟踪


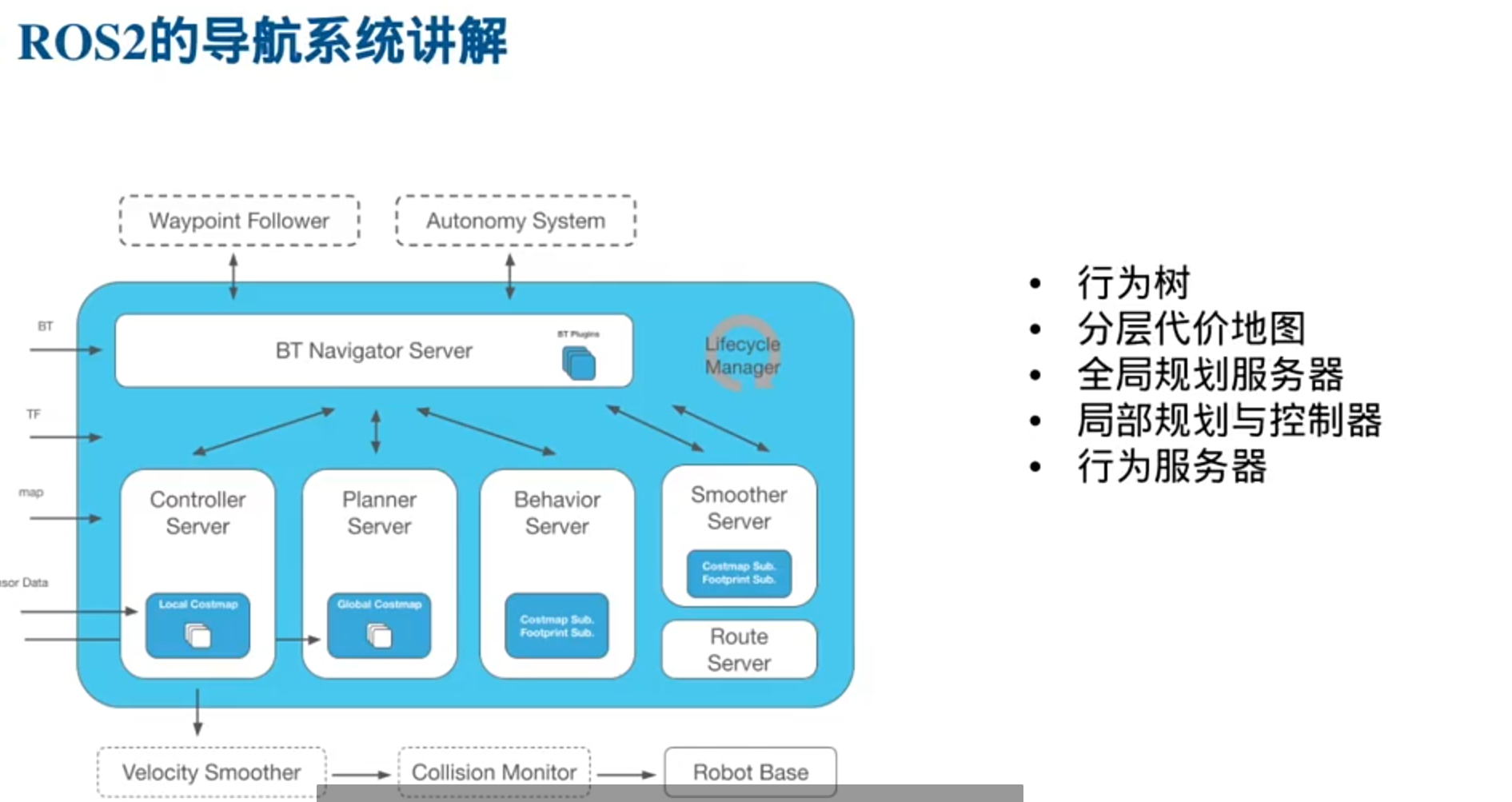
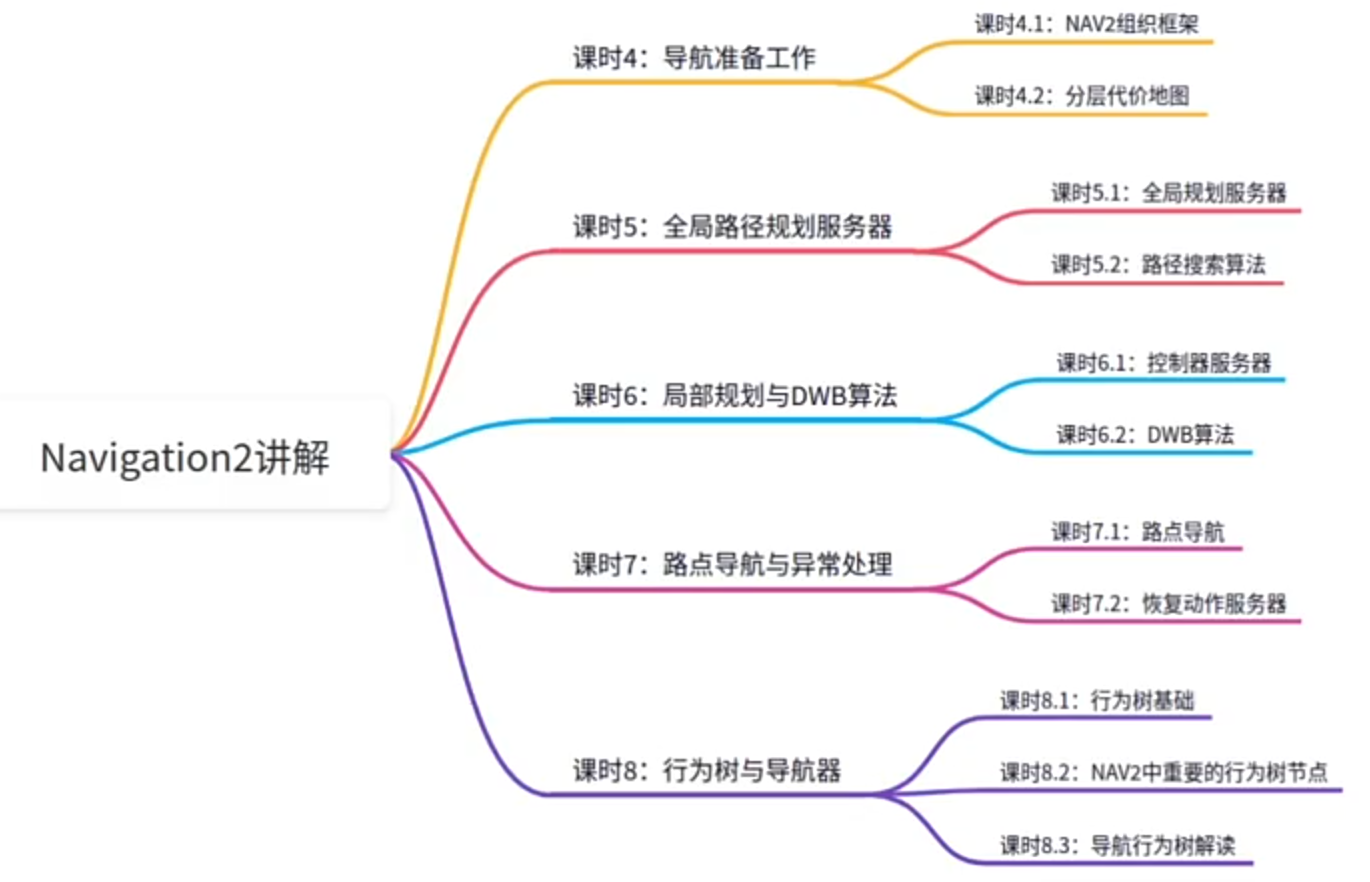
Navigation2组成模块
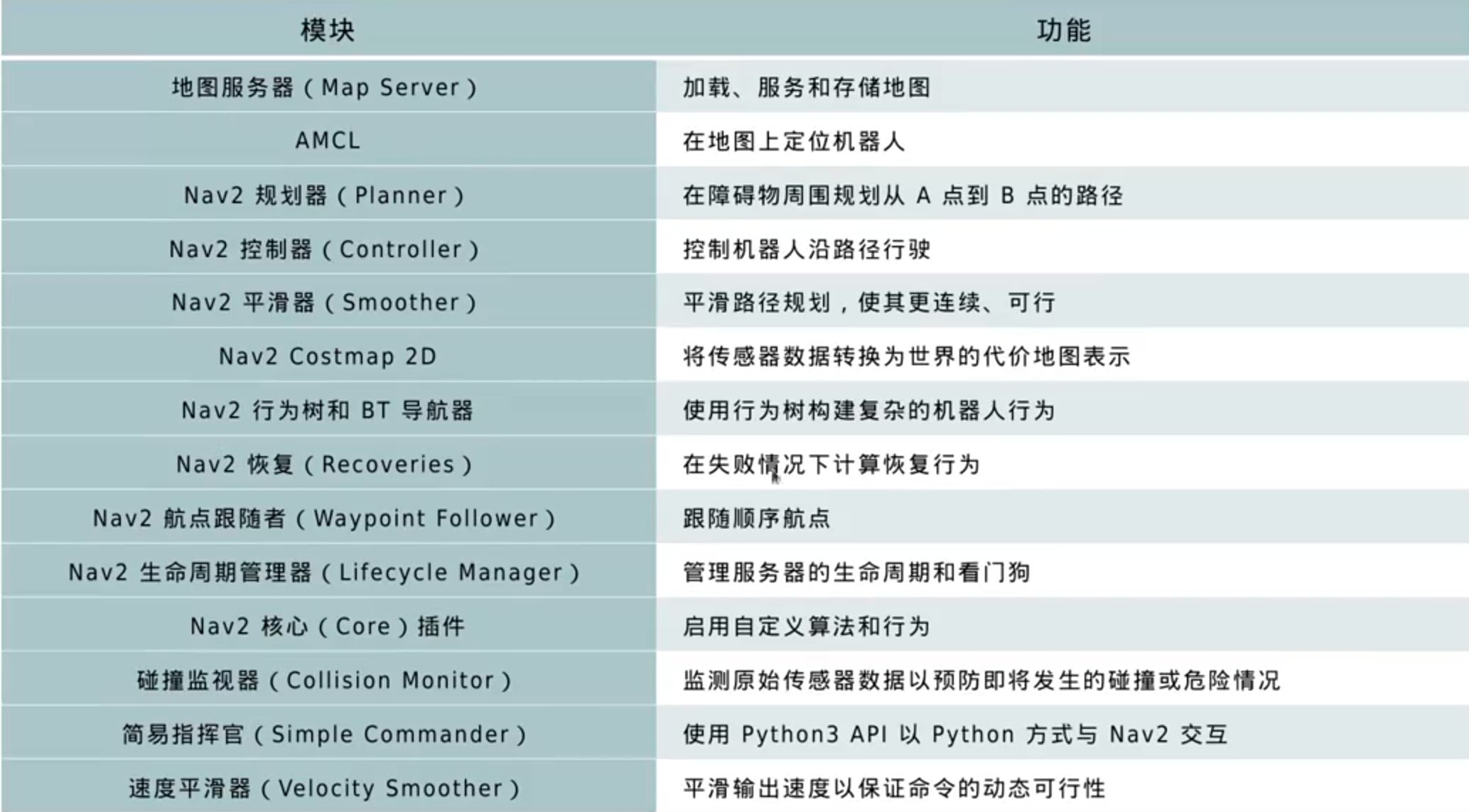
运行流程:
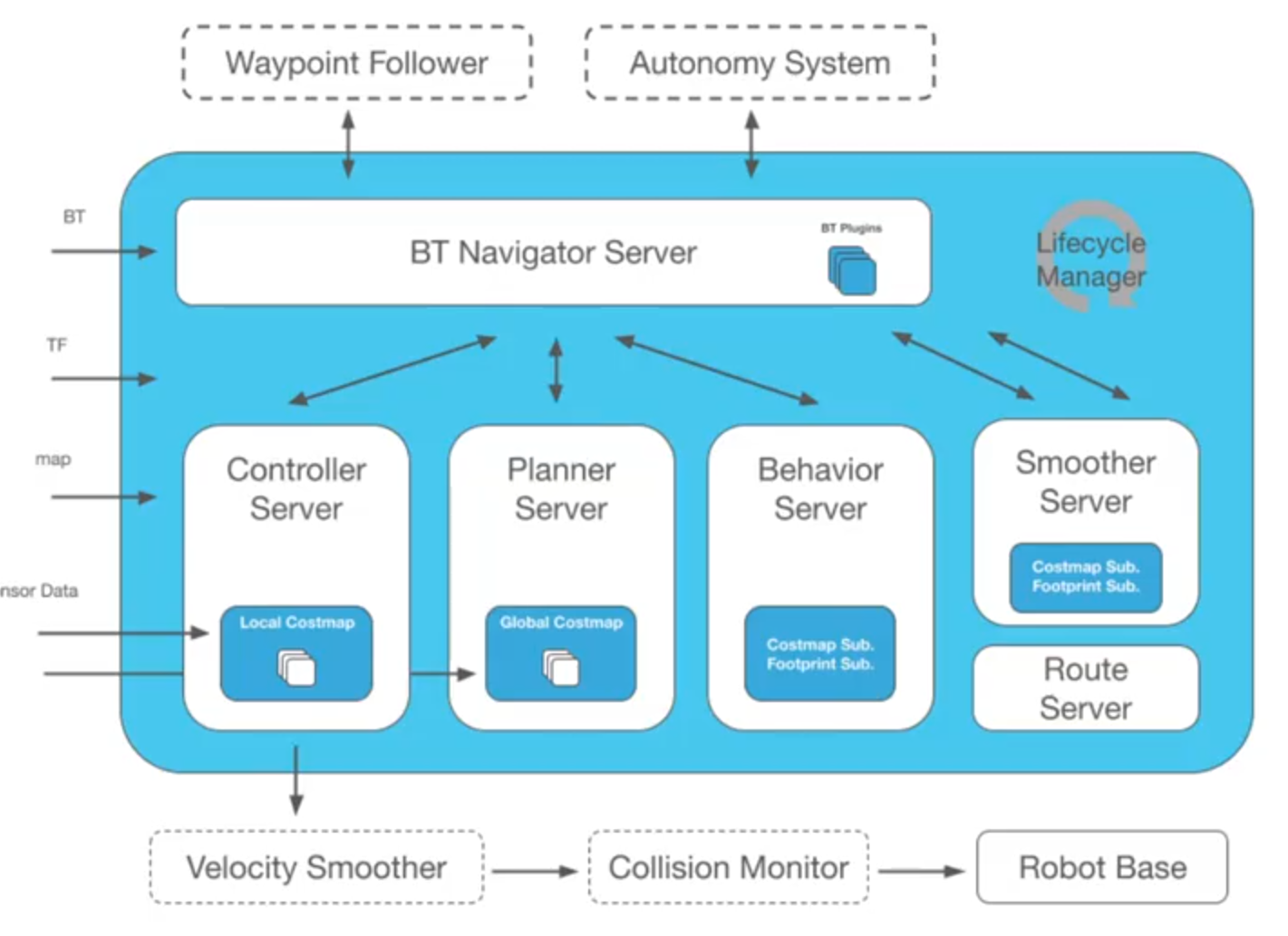
功能包:
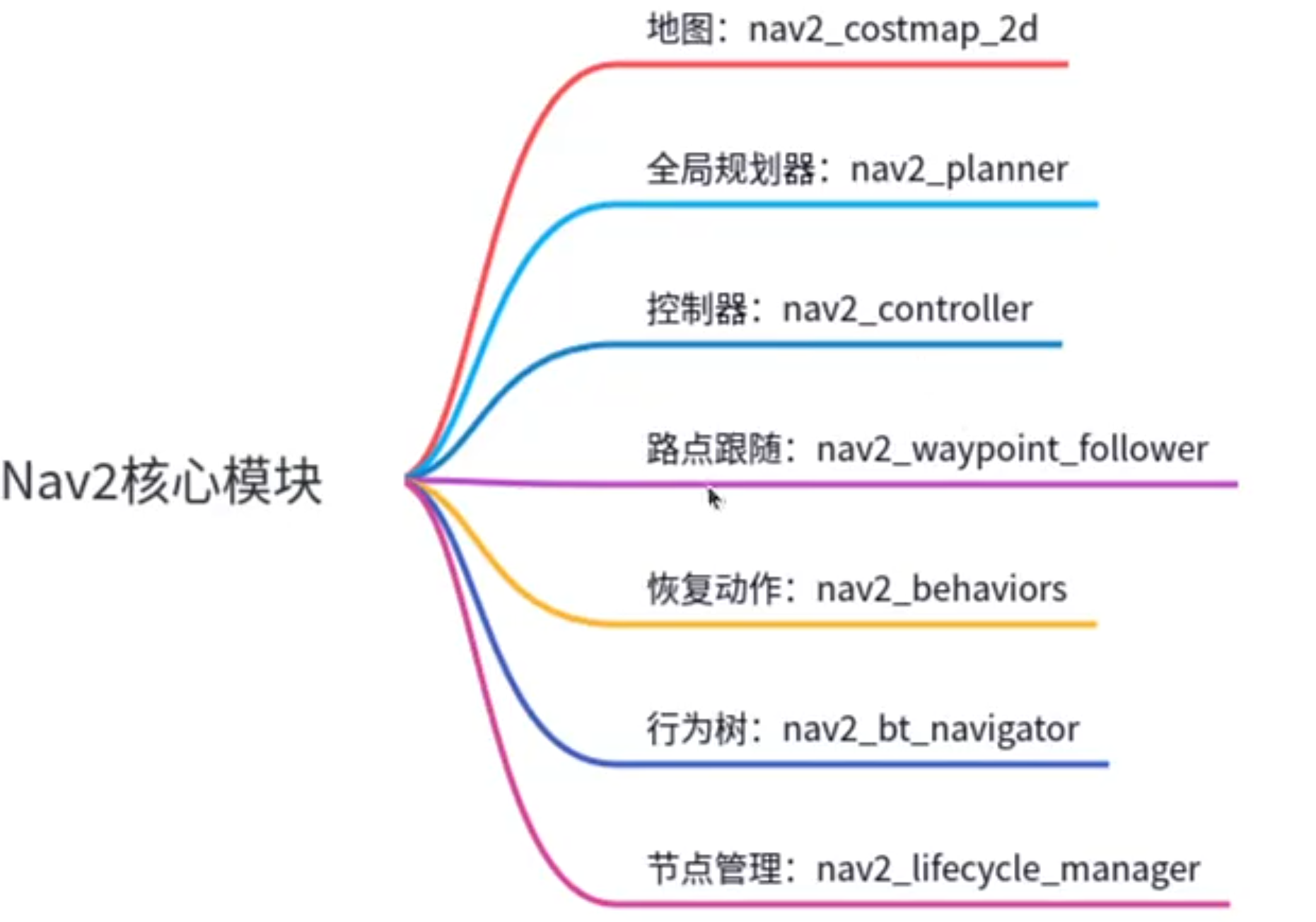
Nav2中的地图
代价地图
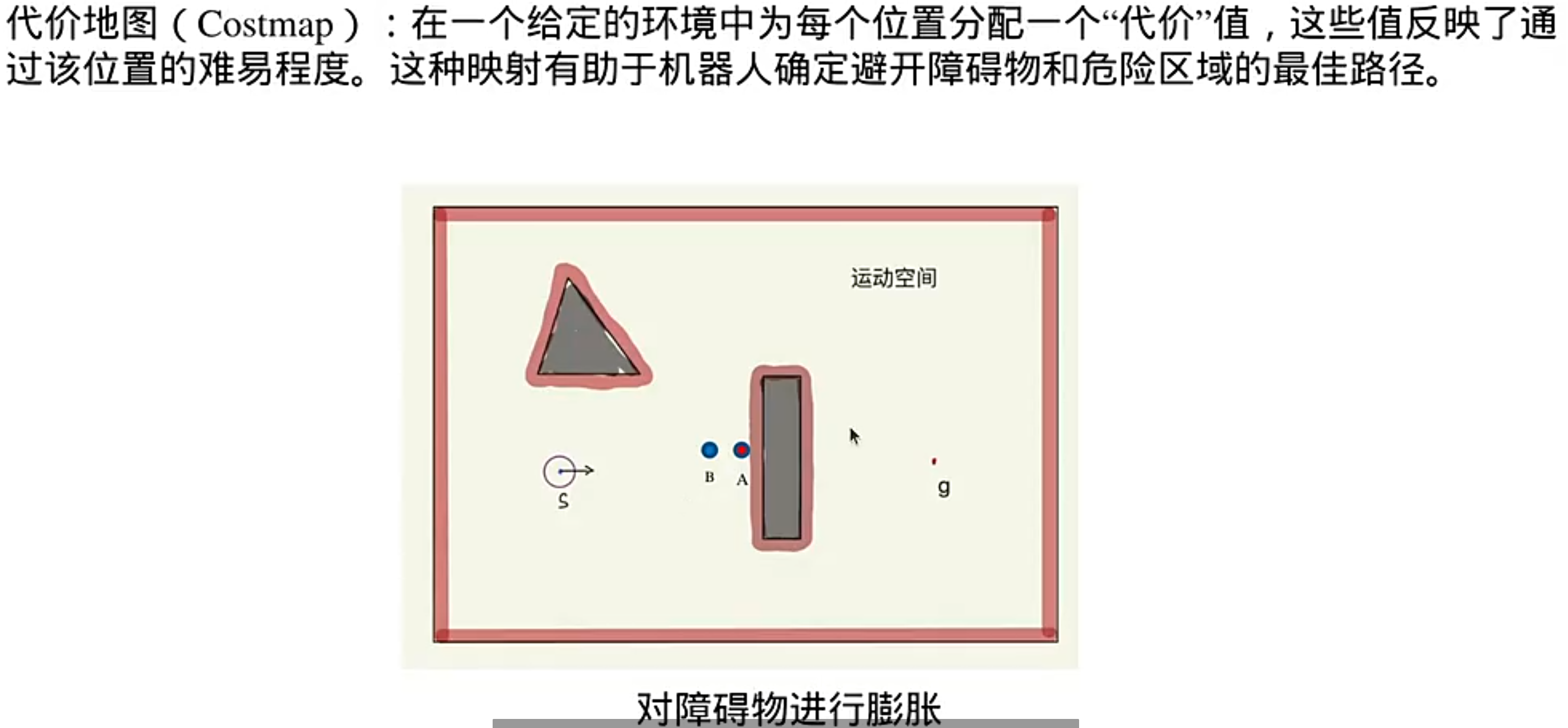
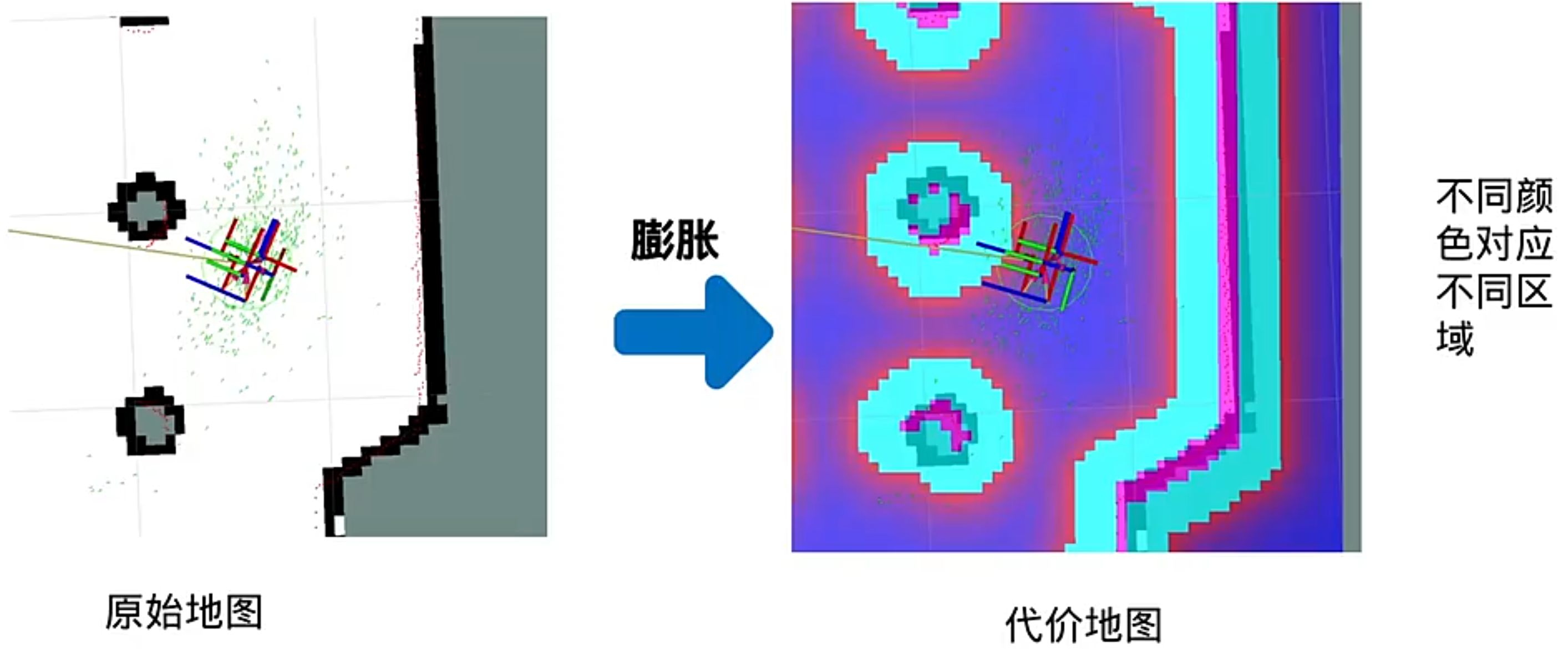
分层代价地图:(直更新有变化的区域)
论文里的分层:

Nav2分层:
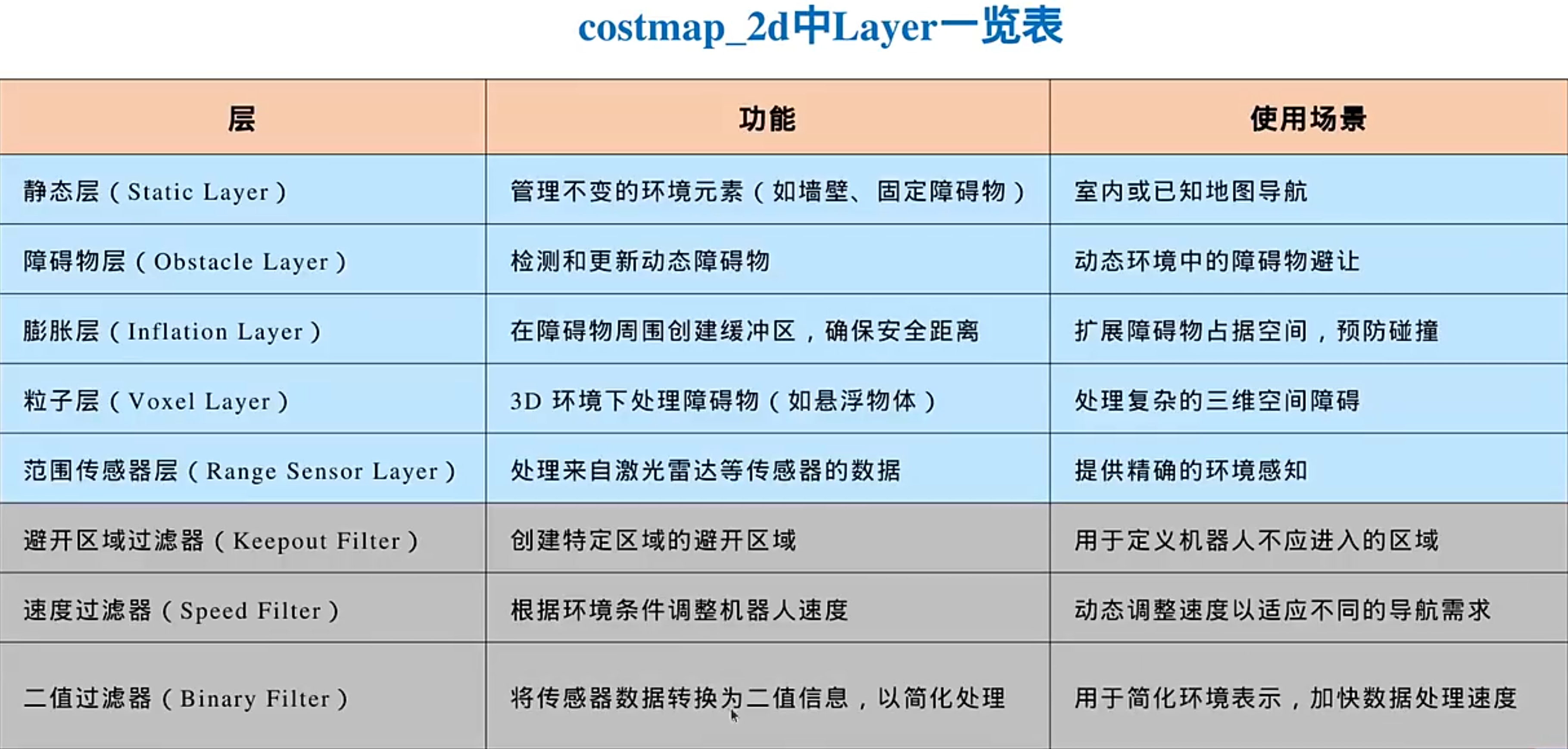
(速度过滤器:限速区)
重启蓝牙服务:
sudo systemctl restart bluetooth
代价地图局部更新的过程:
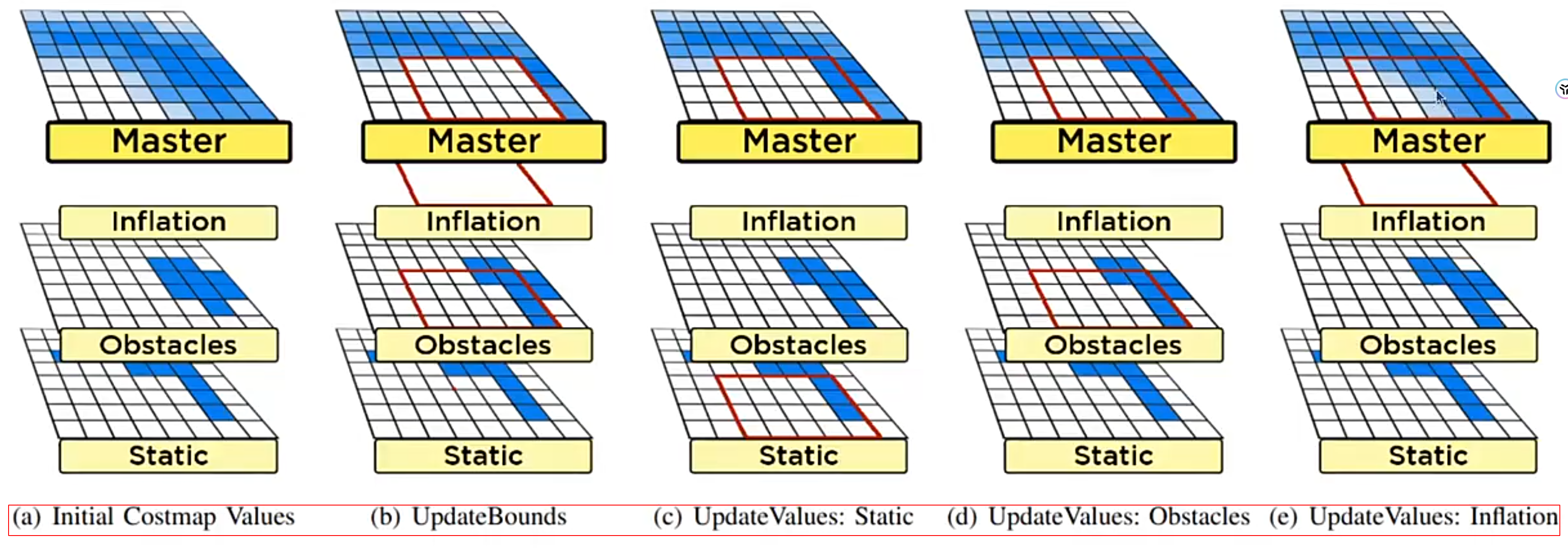
更新边界,更新值
Nav2的核心特点是使用插件机制,插件机制的实现过程是每个层去继承一个基类
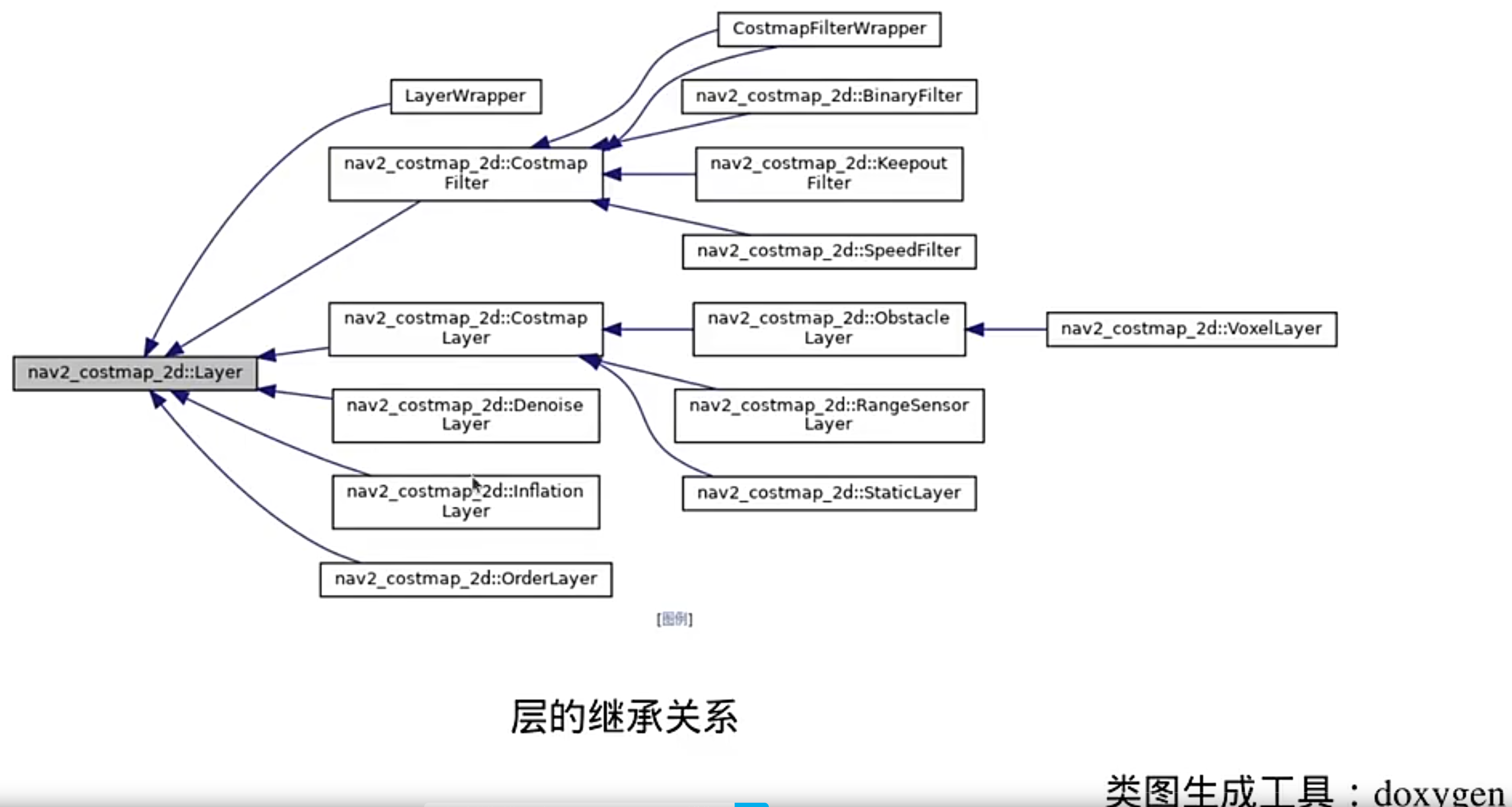

膨胀层具体实现:
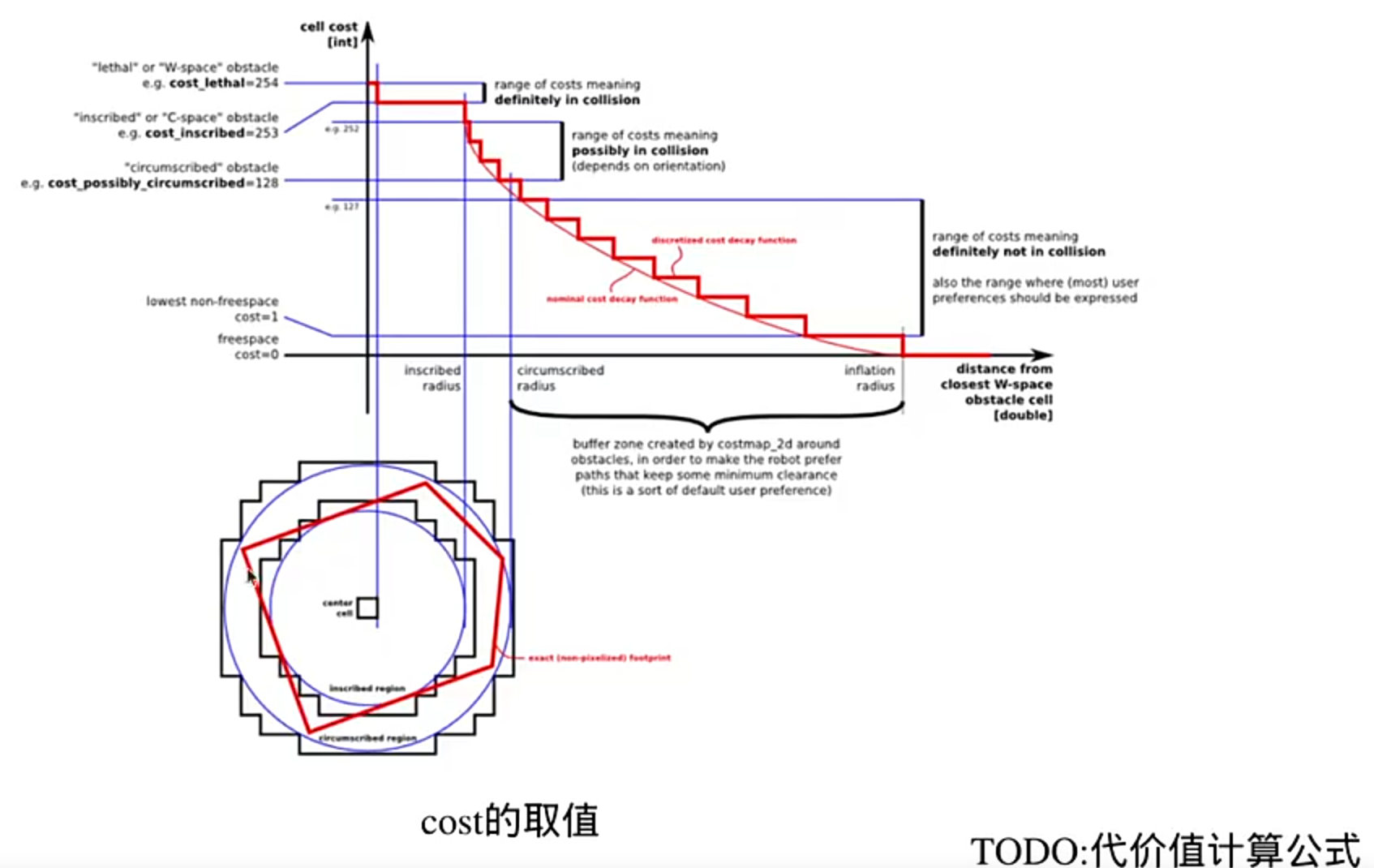

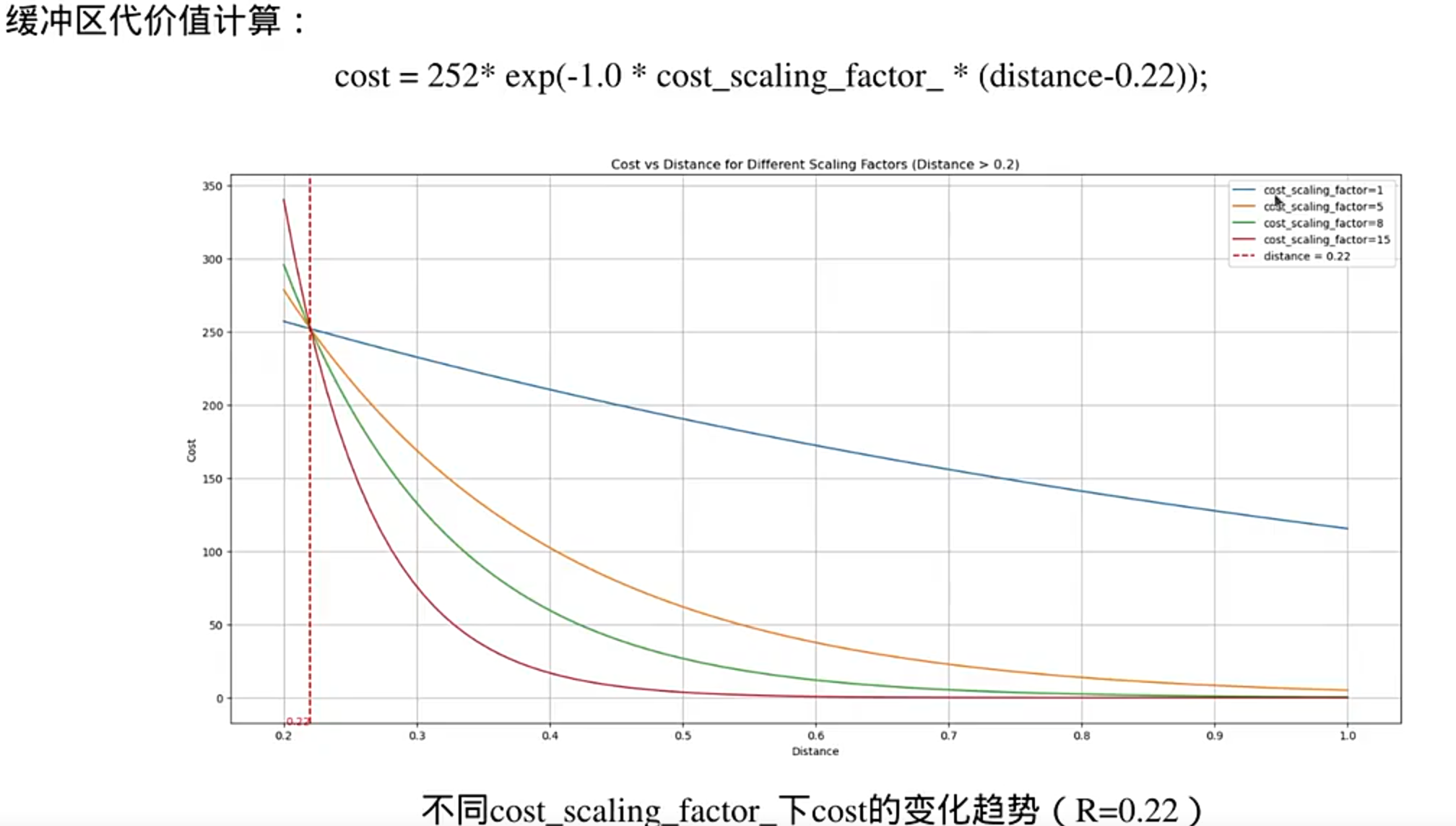
限速区具体实现:
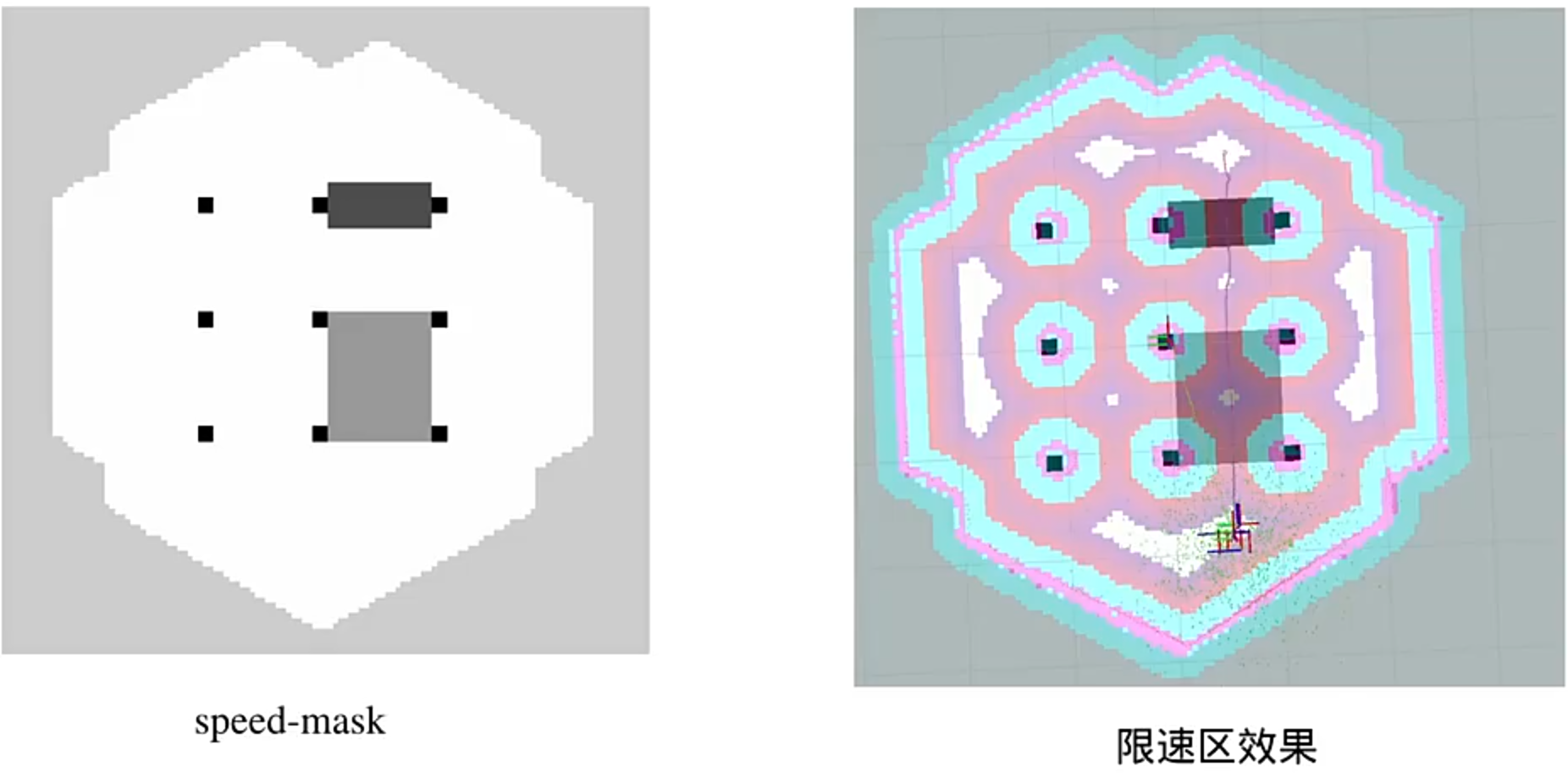
配置参数
机器人坐标系:
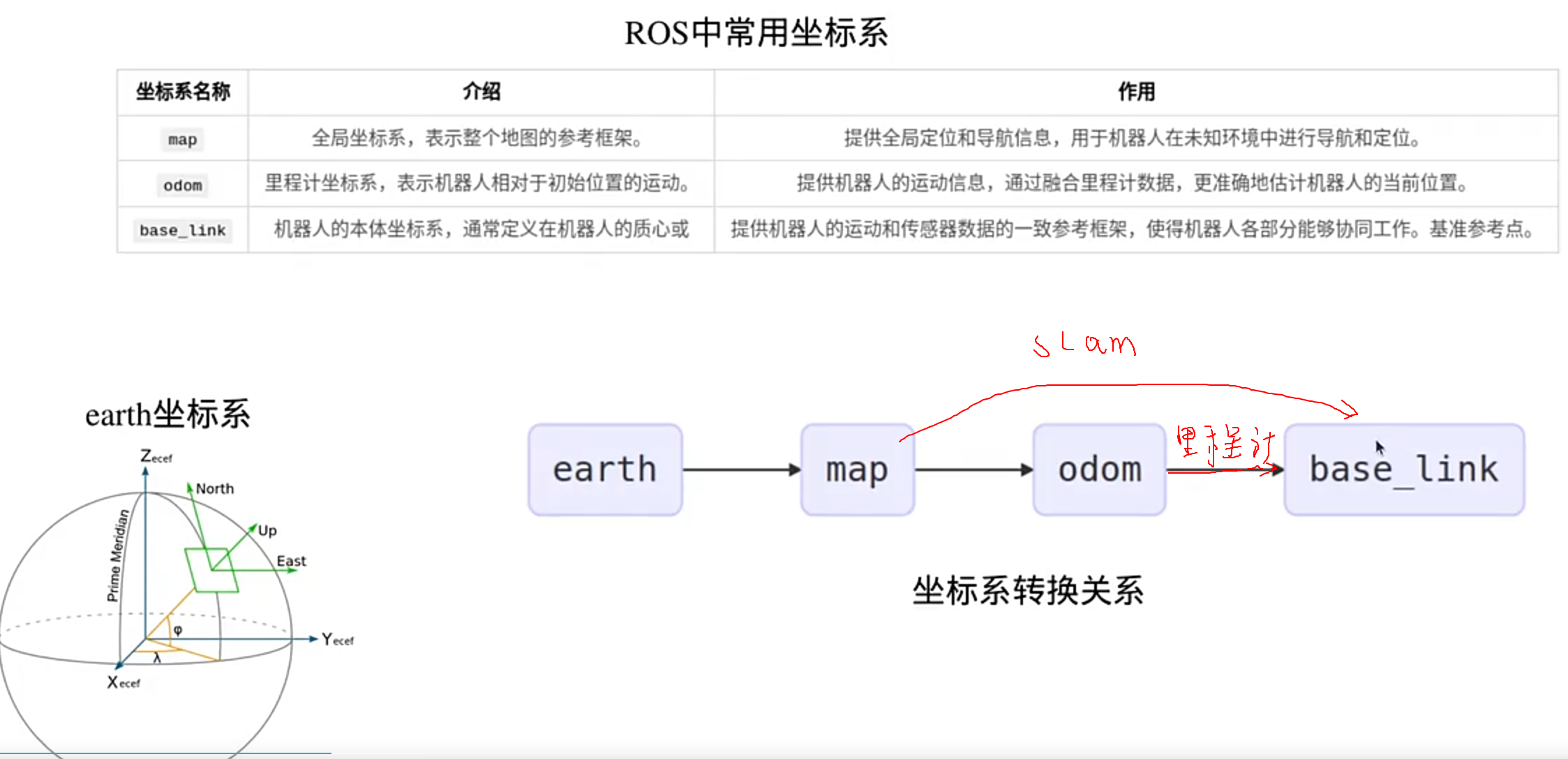
(TF树里只能有一个parent)
代价地图有两张:
全局路径搜索(静态),局部轨迹优化(动态)
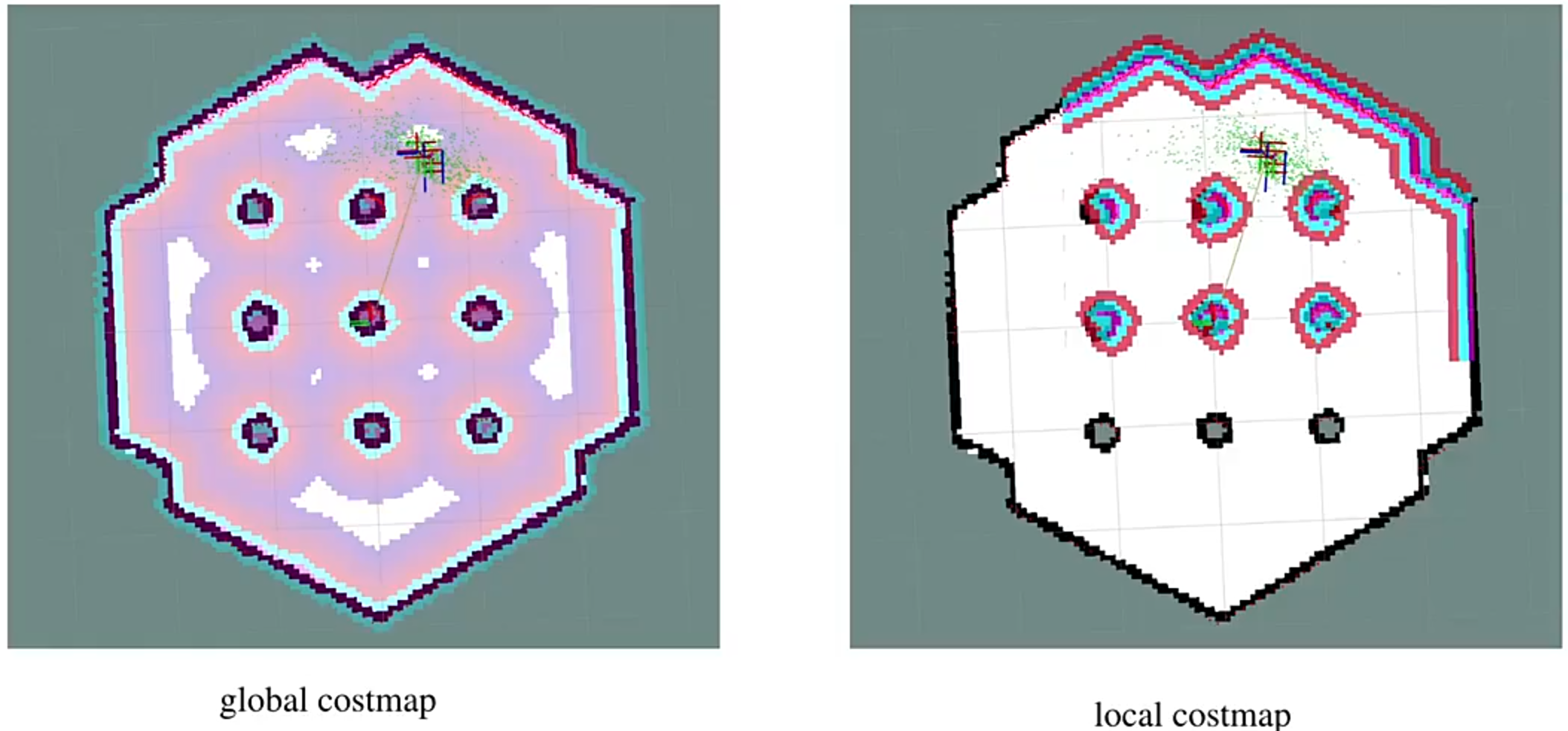
全局代价地图参数:

局部代价地图参数:
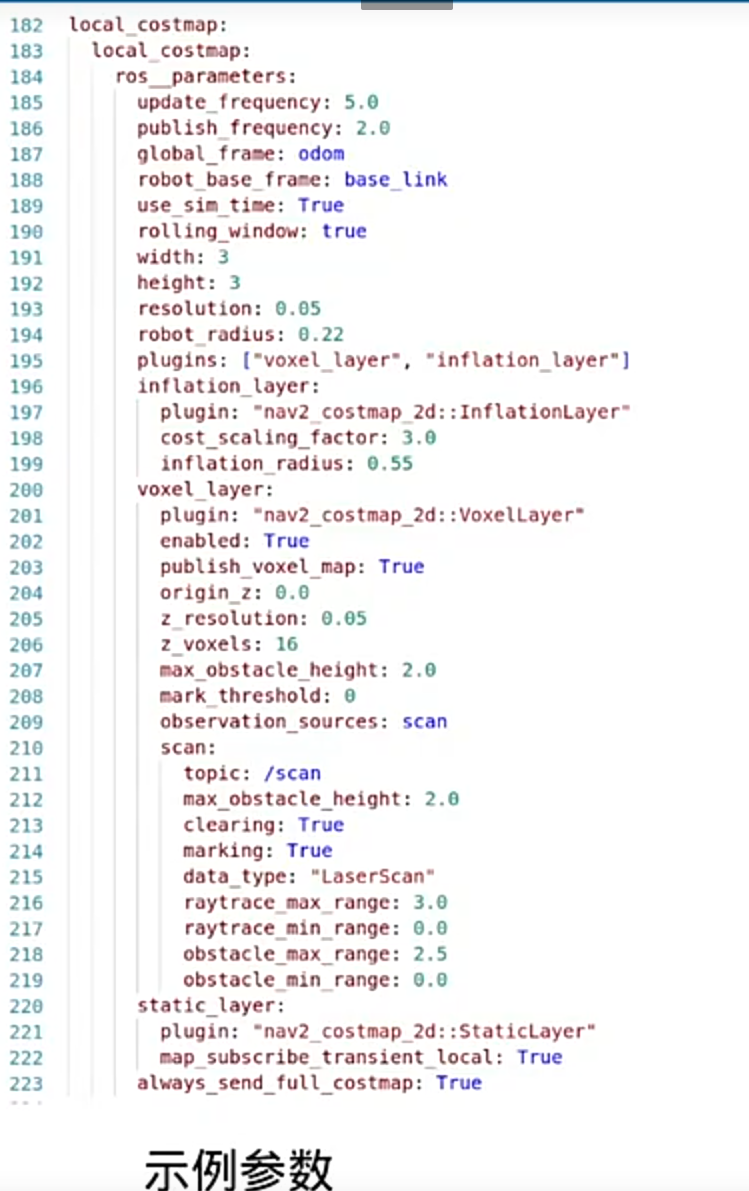
footprint 是机器人在环境中占据的空间的几何形状。这个形状通常用一组坐标点来表示,形成一个多边形。
resolution=0.05 表示地图的分辨率。指每个栅格(grid cell)的大小,以米为单位
全局路径规划服务器
Planner_Server的功能
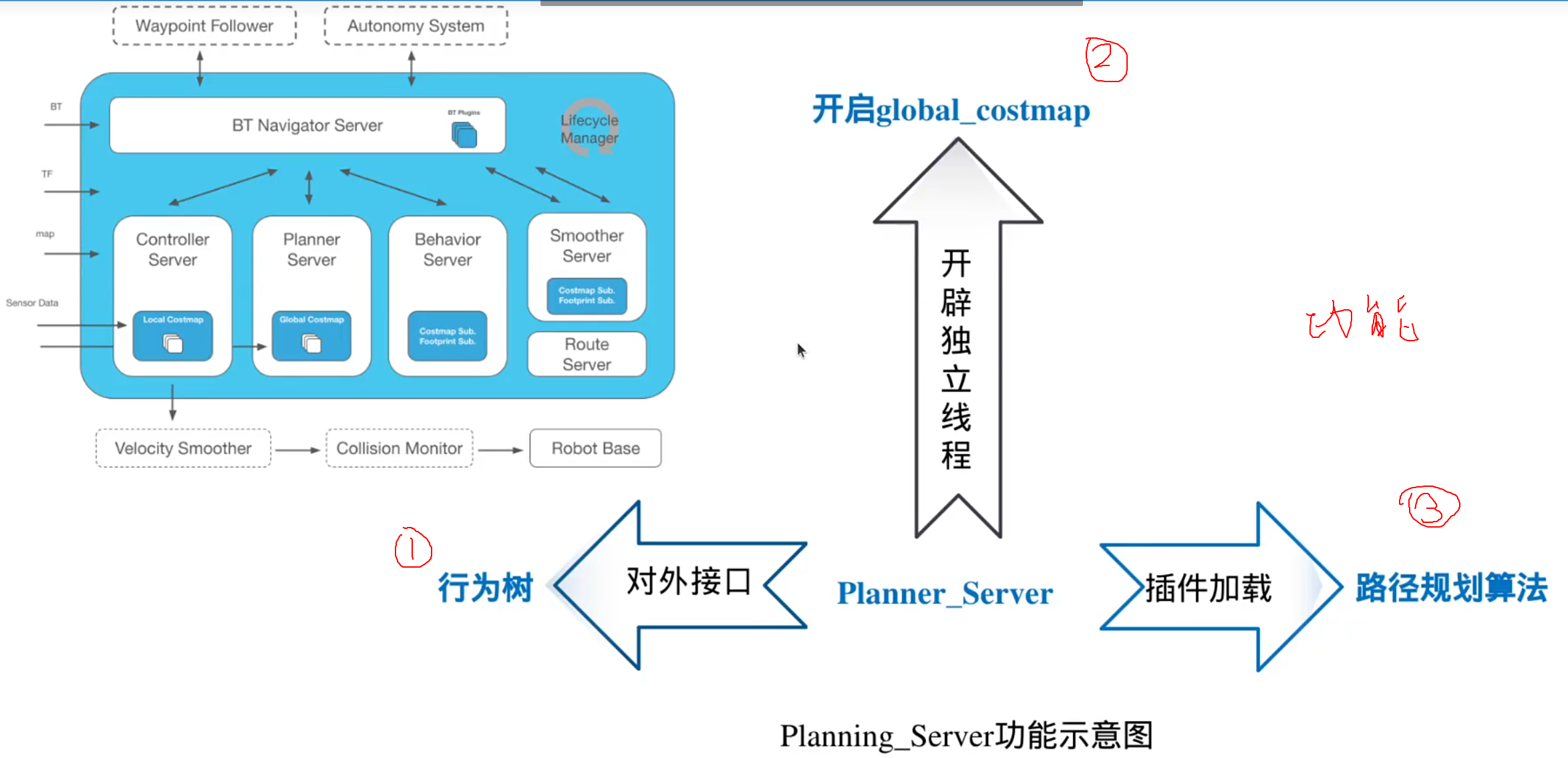
1.对行为树接口:

(navigation2里面使用了大量的action通信机制)

2,开启全局代价地图
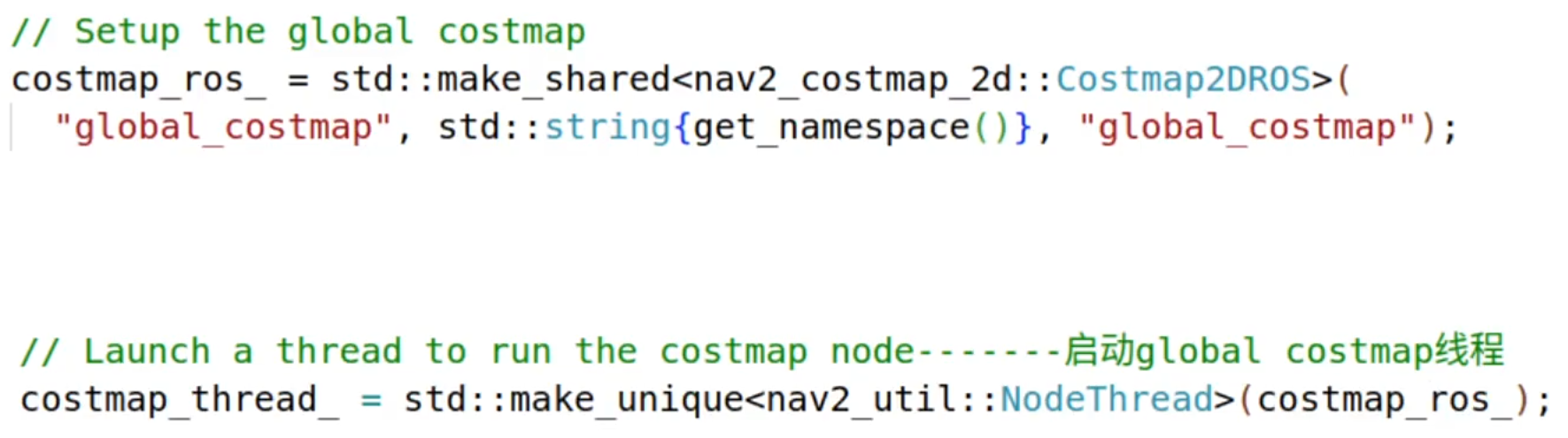
3.加载规划算法
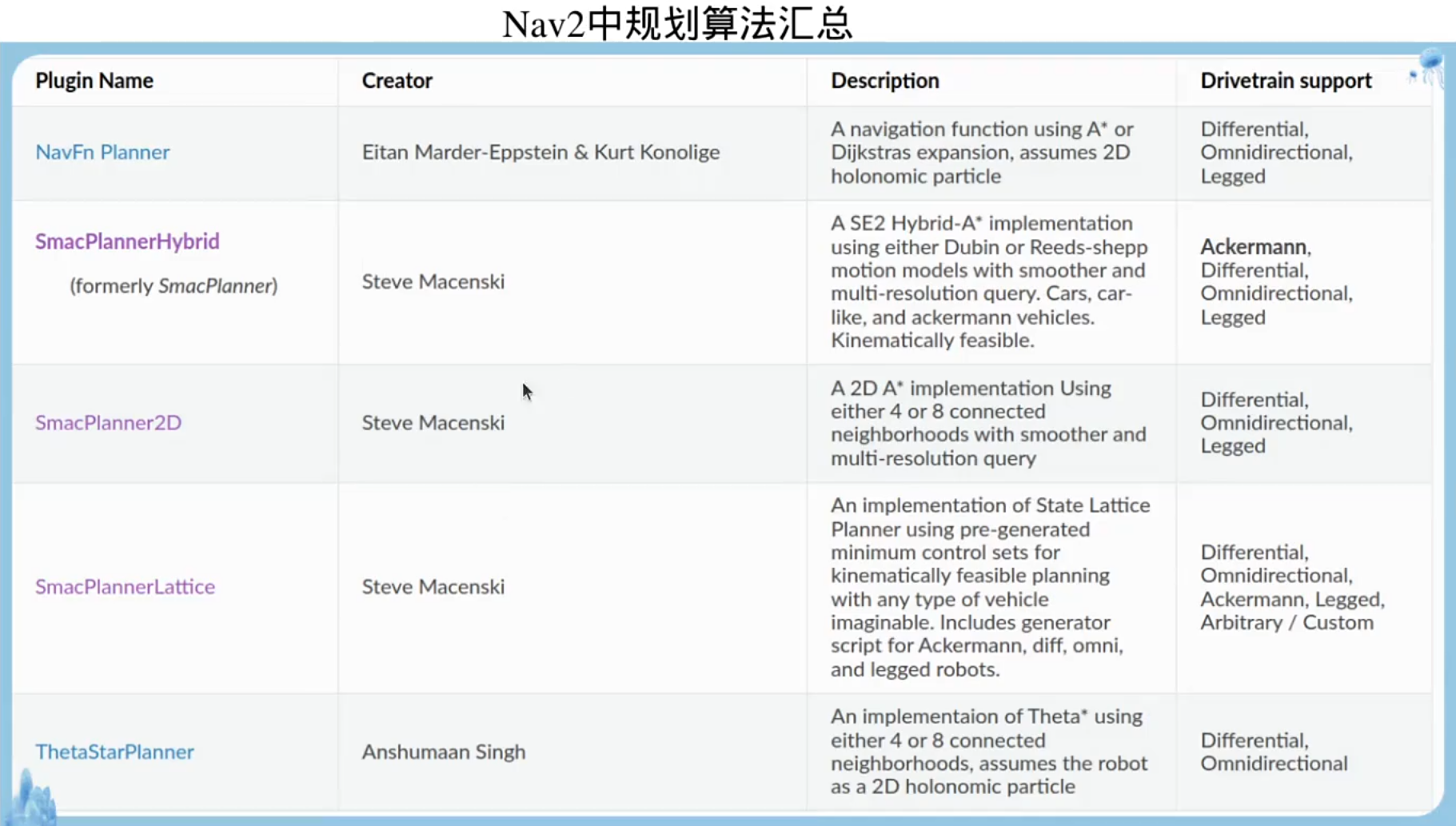
插件机制:
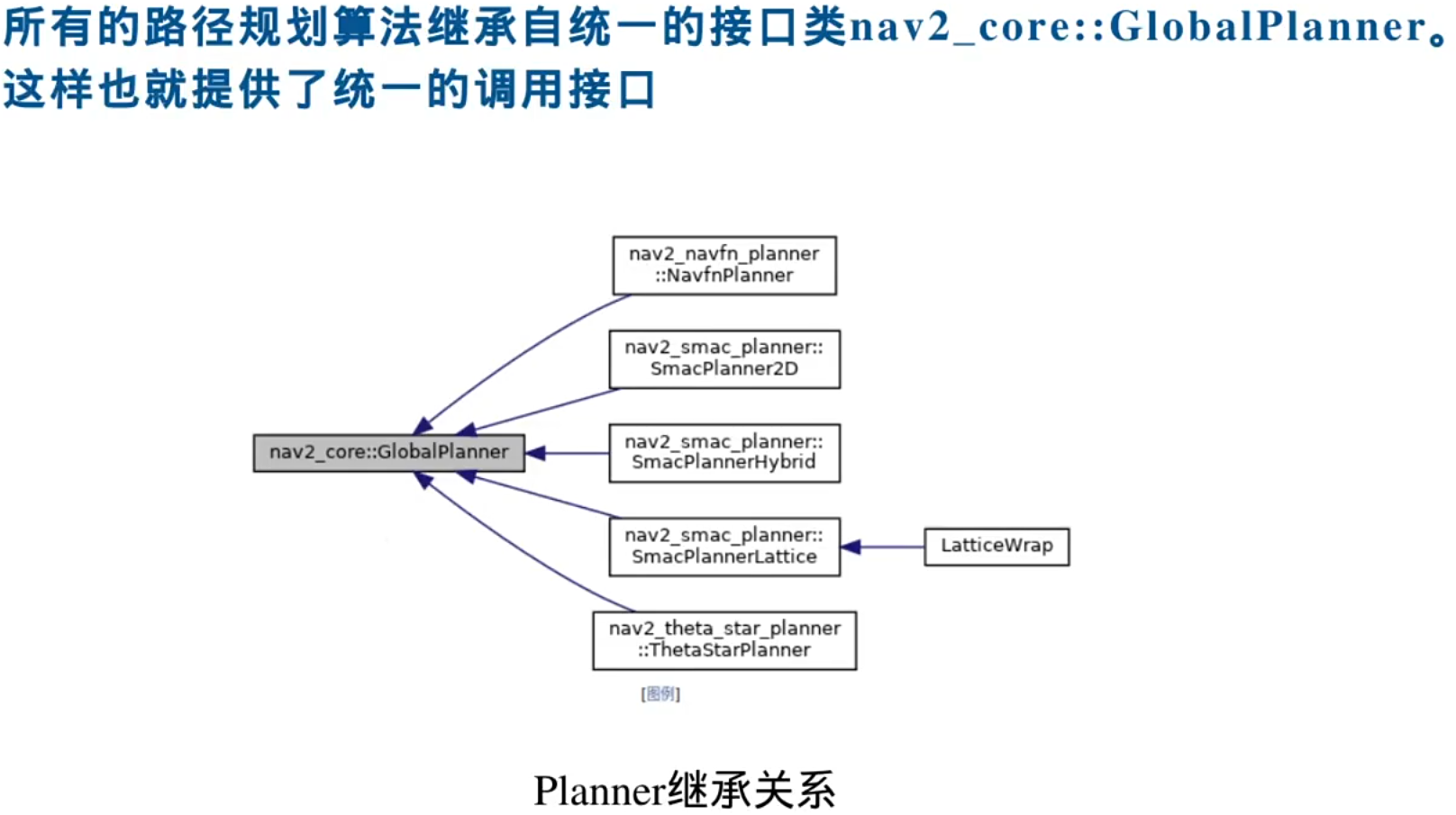
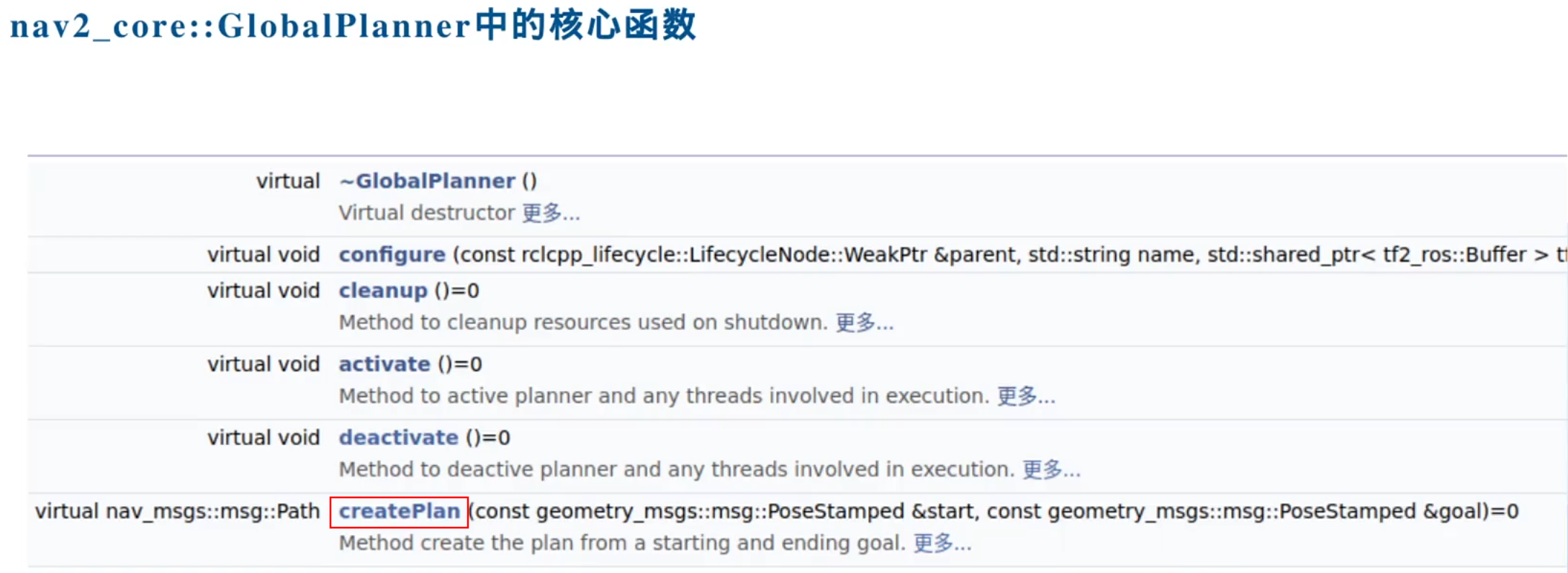
planning_server的源码实现:
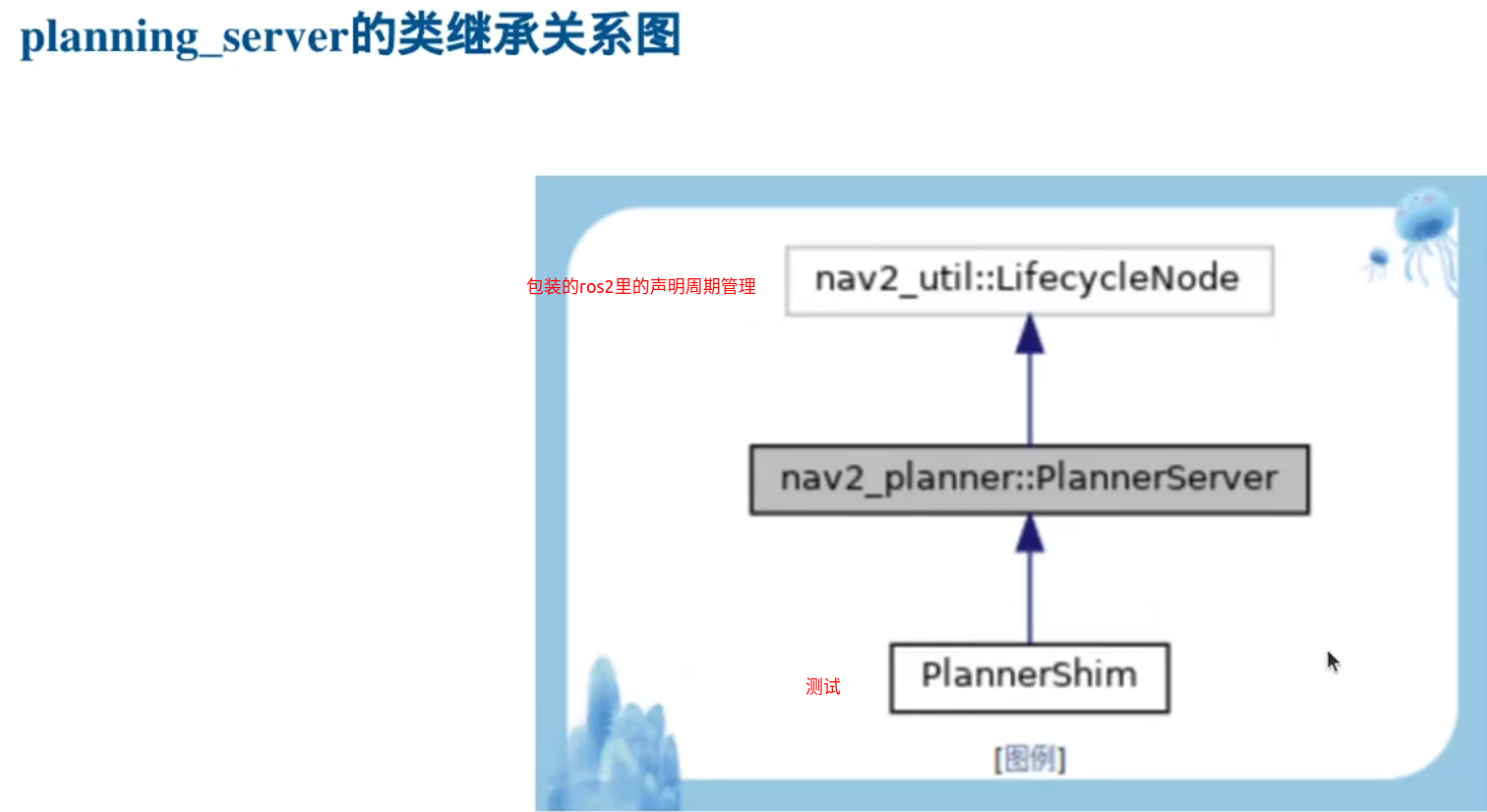
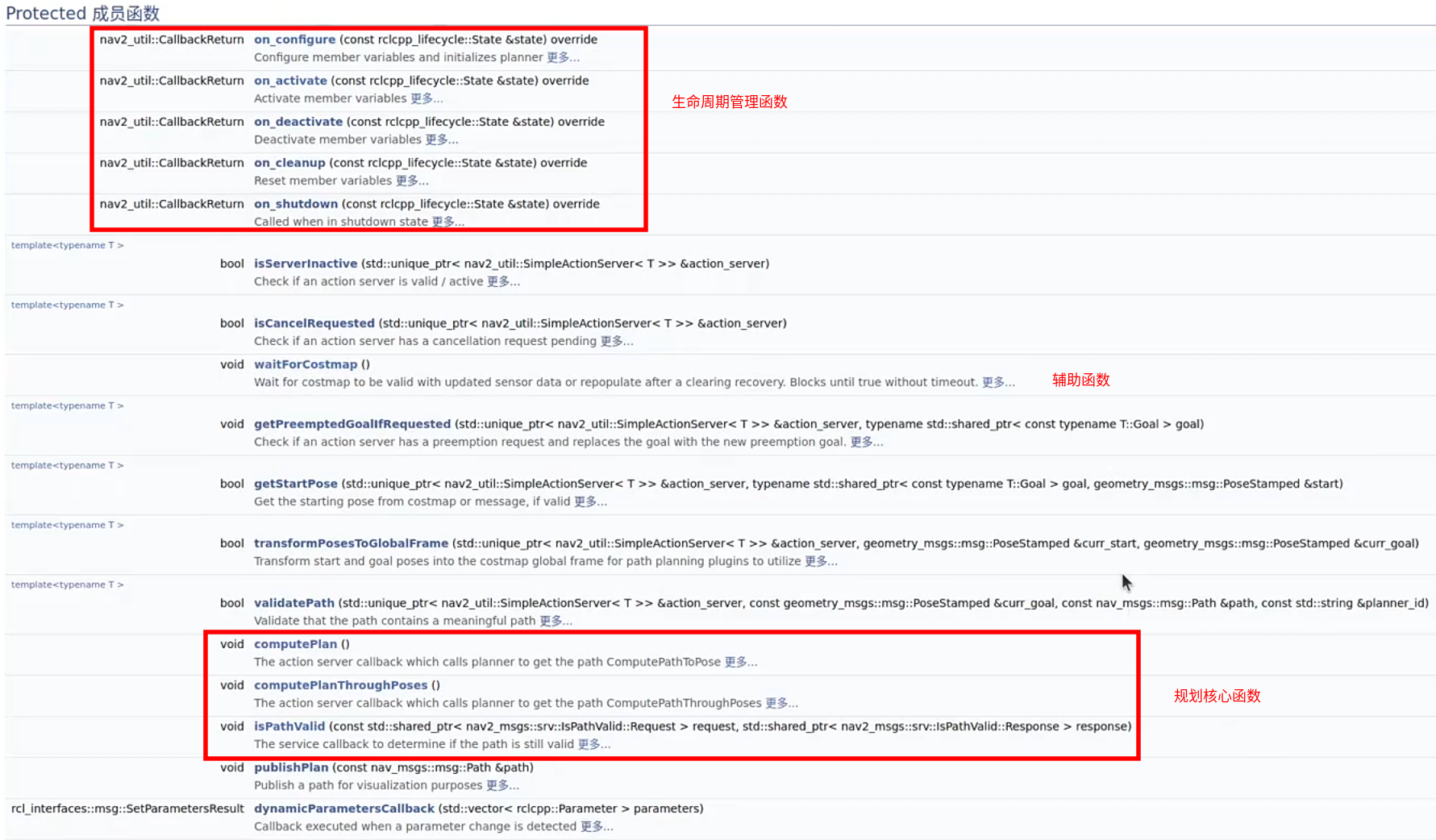

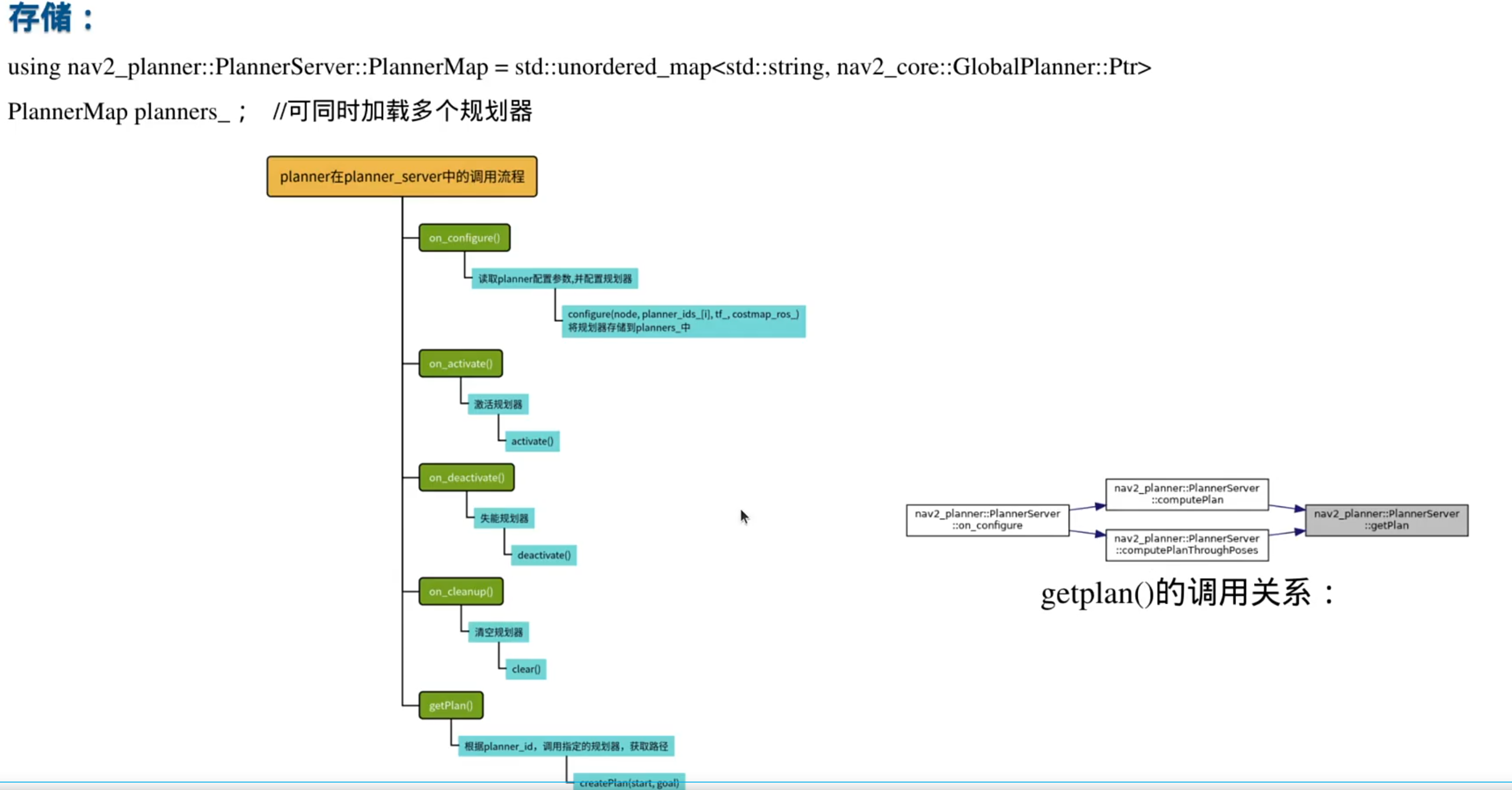
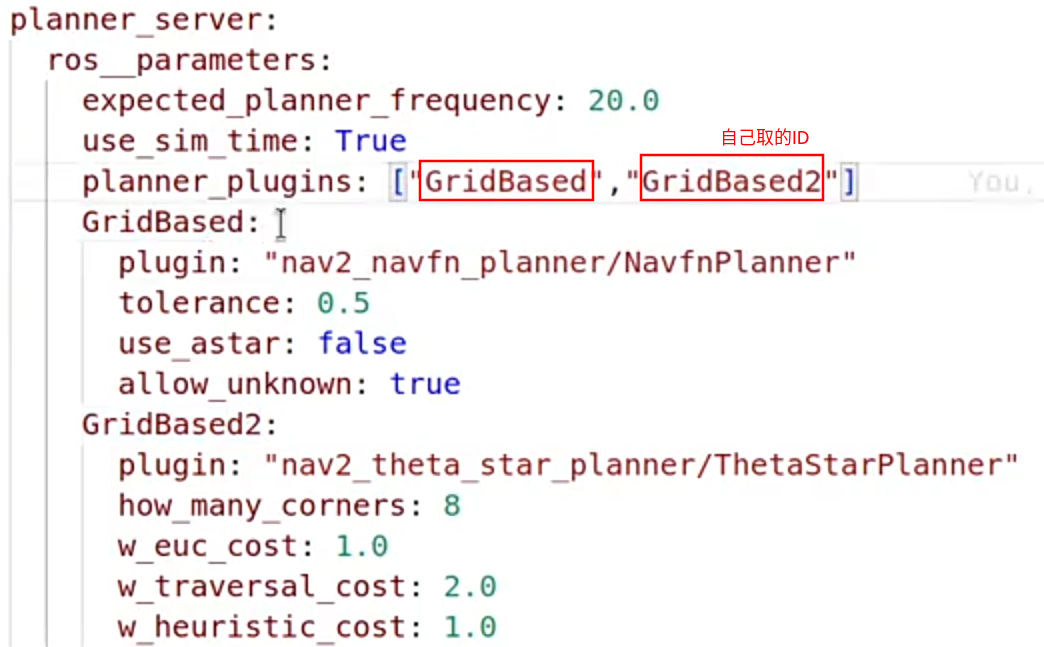
planner_server参数配置

Controller_Server
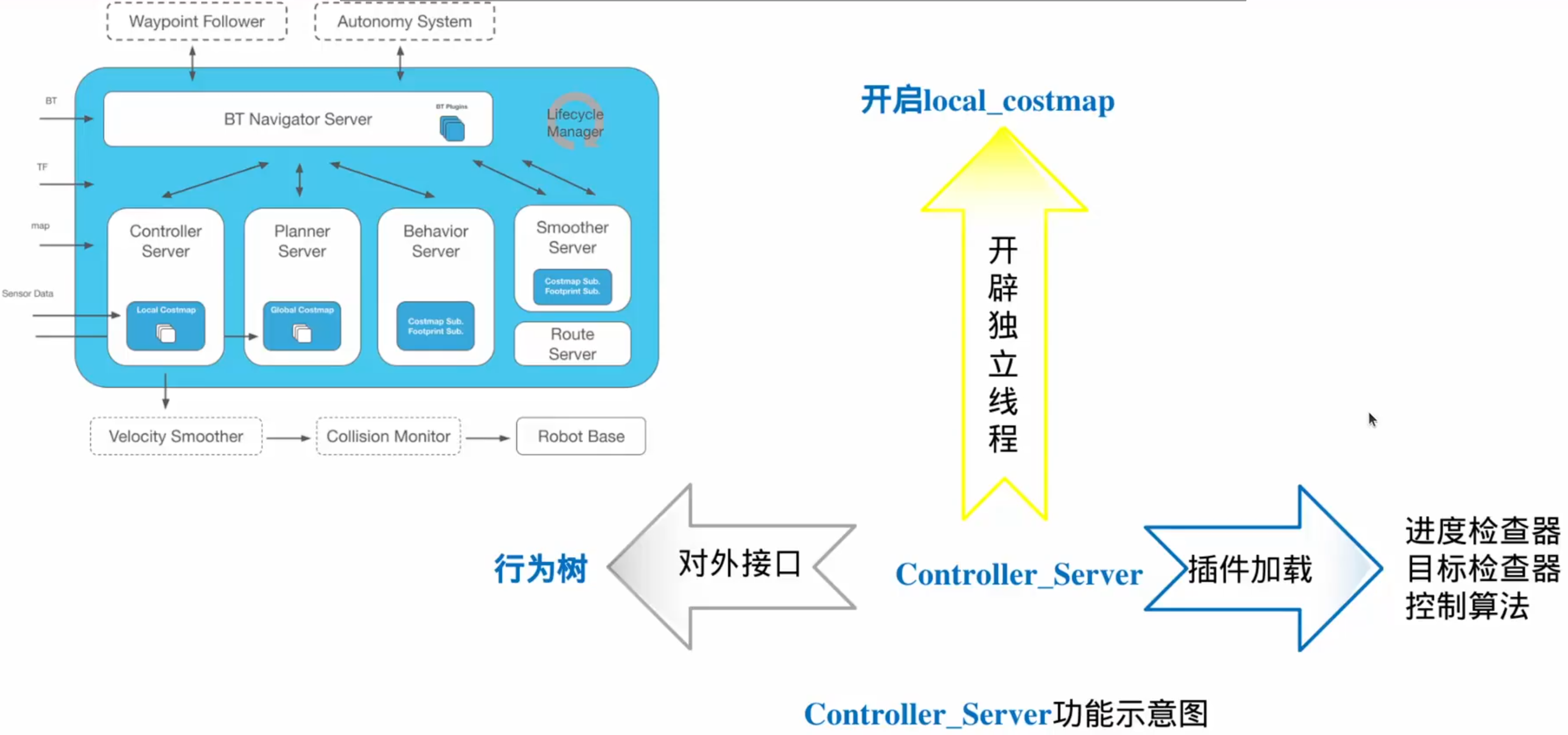
1.接口回调函数(给行为树调用)

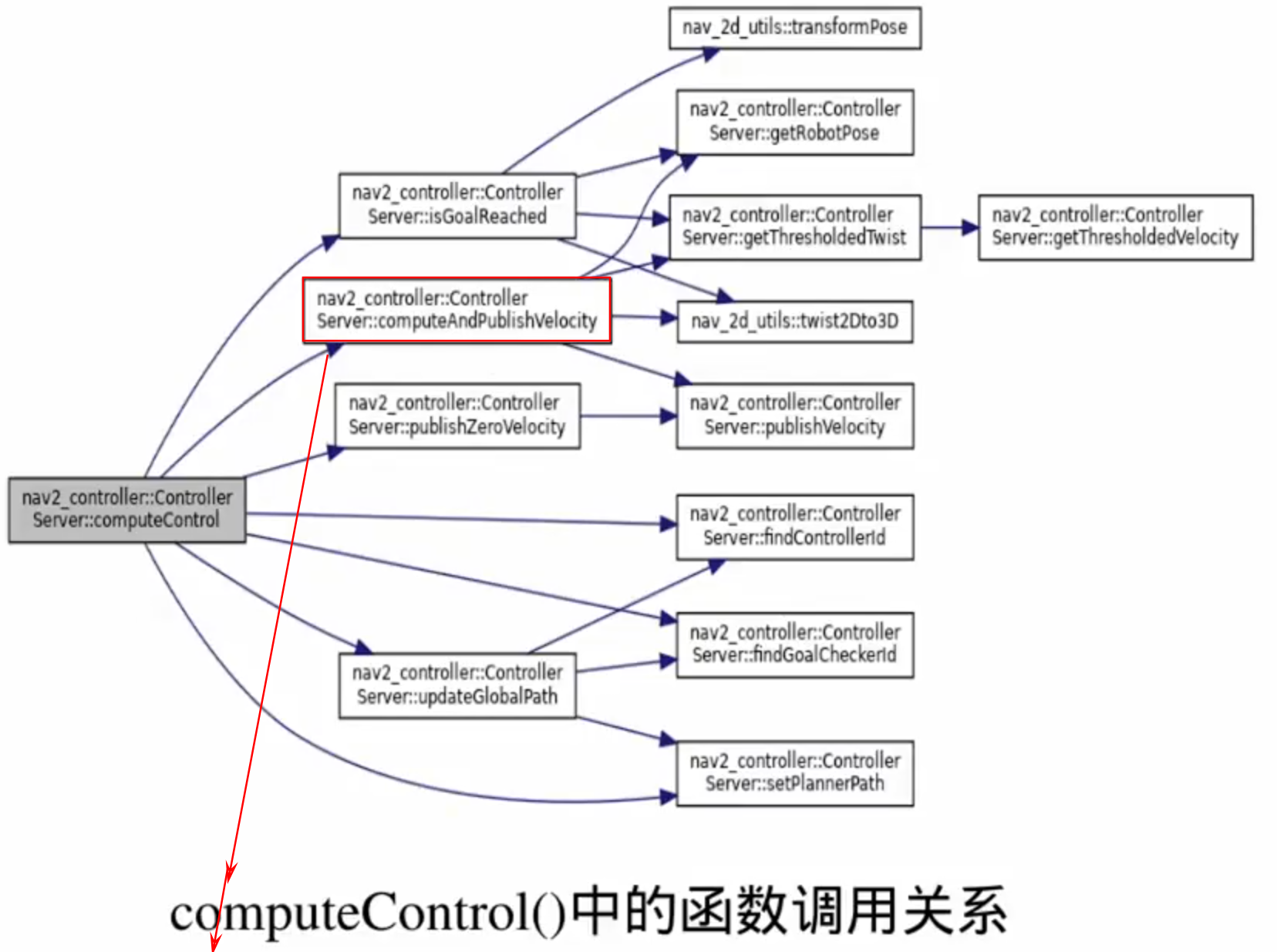
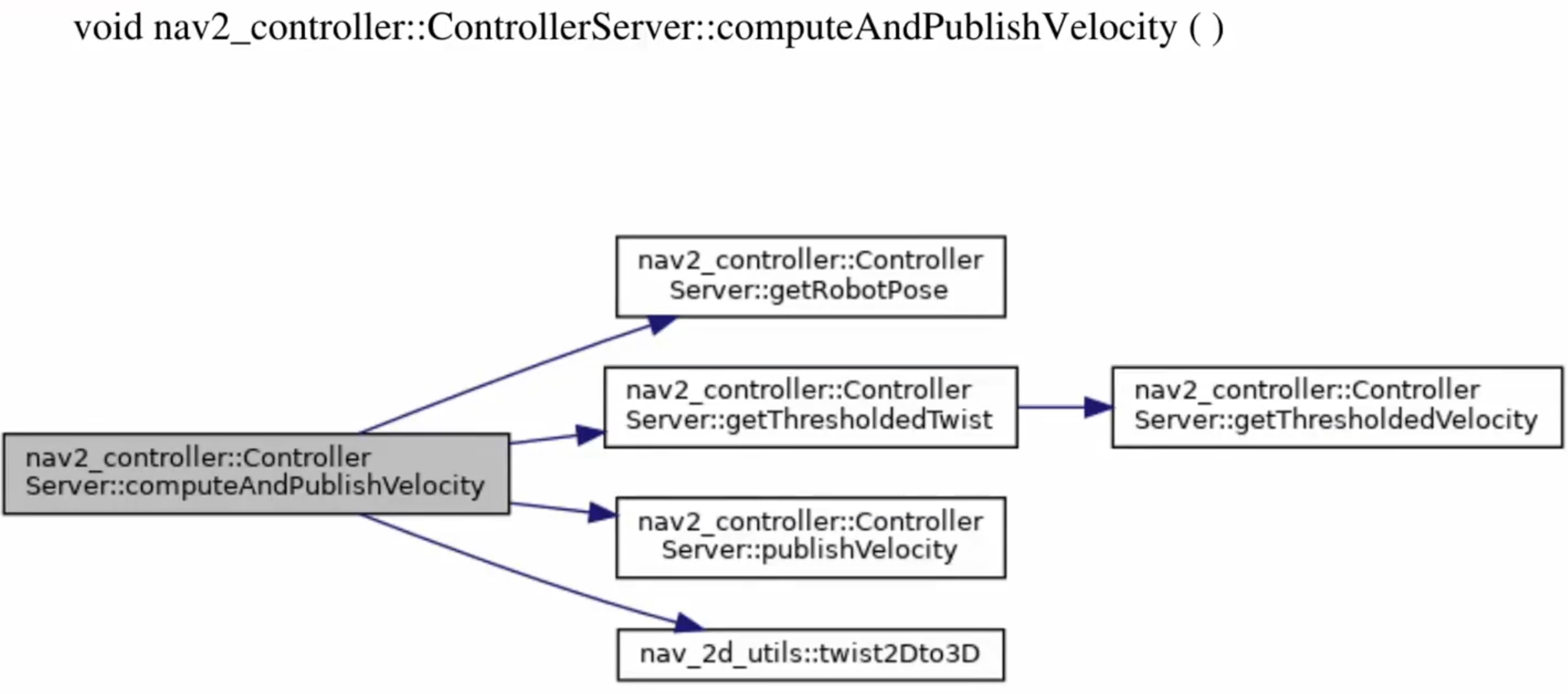
2.控制器插件

重要插件–进度检查器
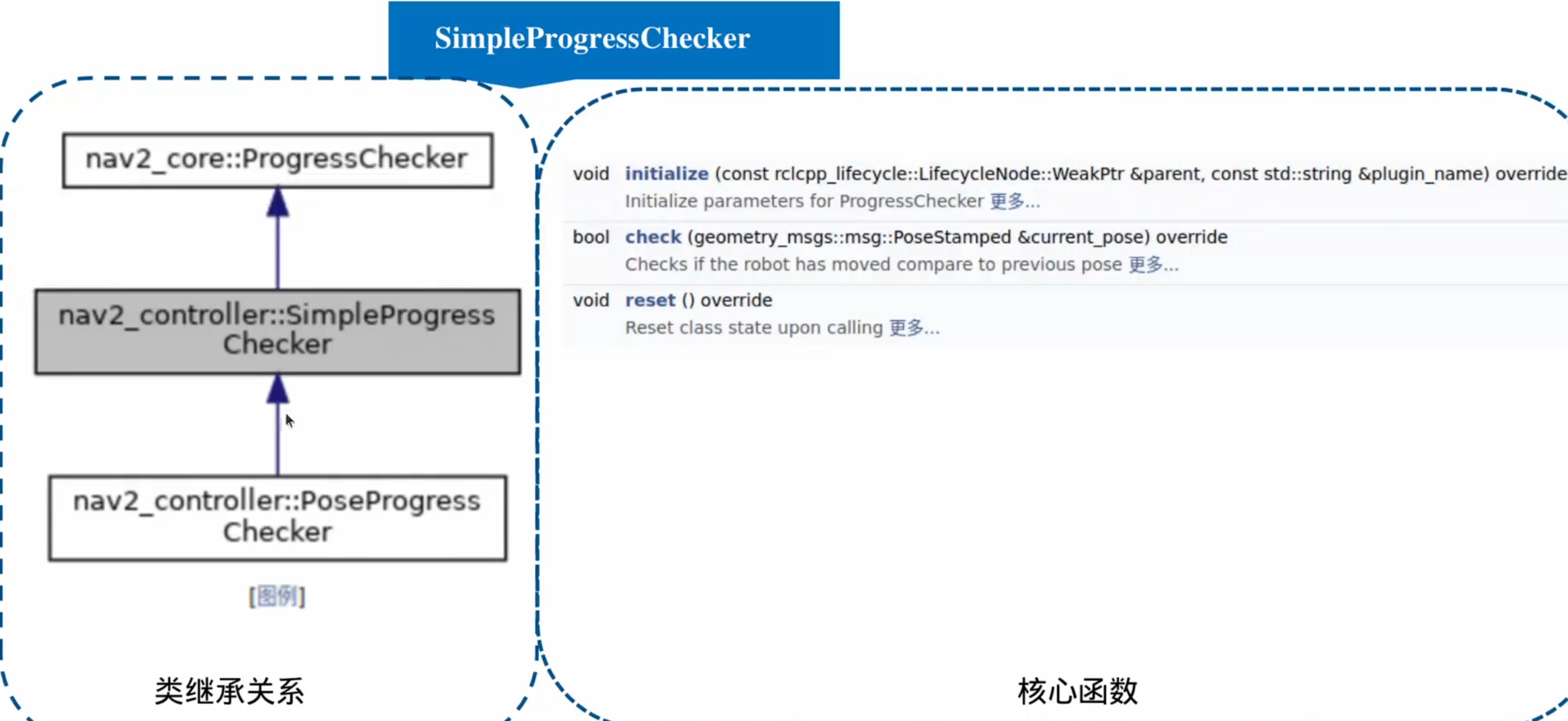
重要插件–目标检查器
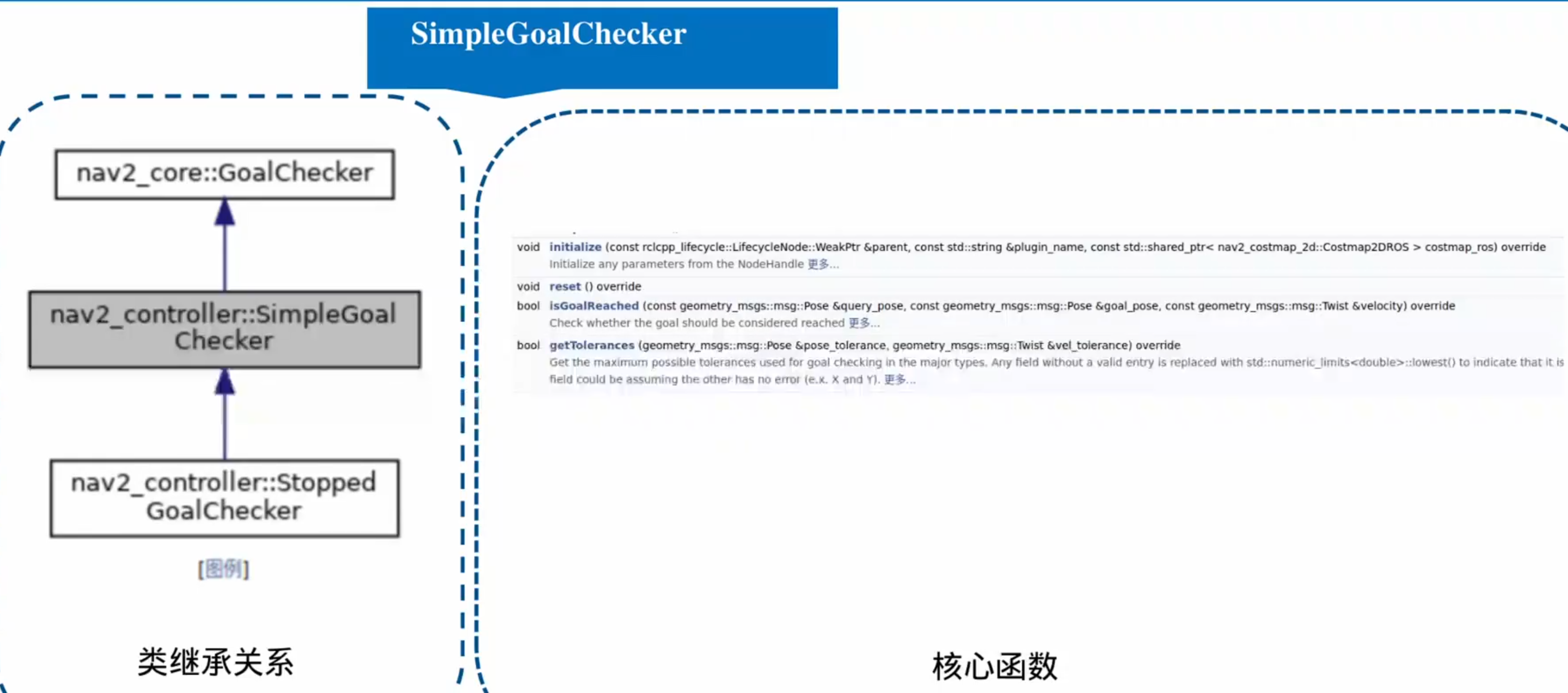
控制流程:
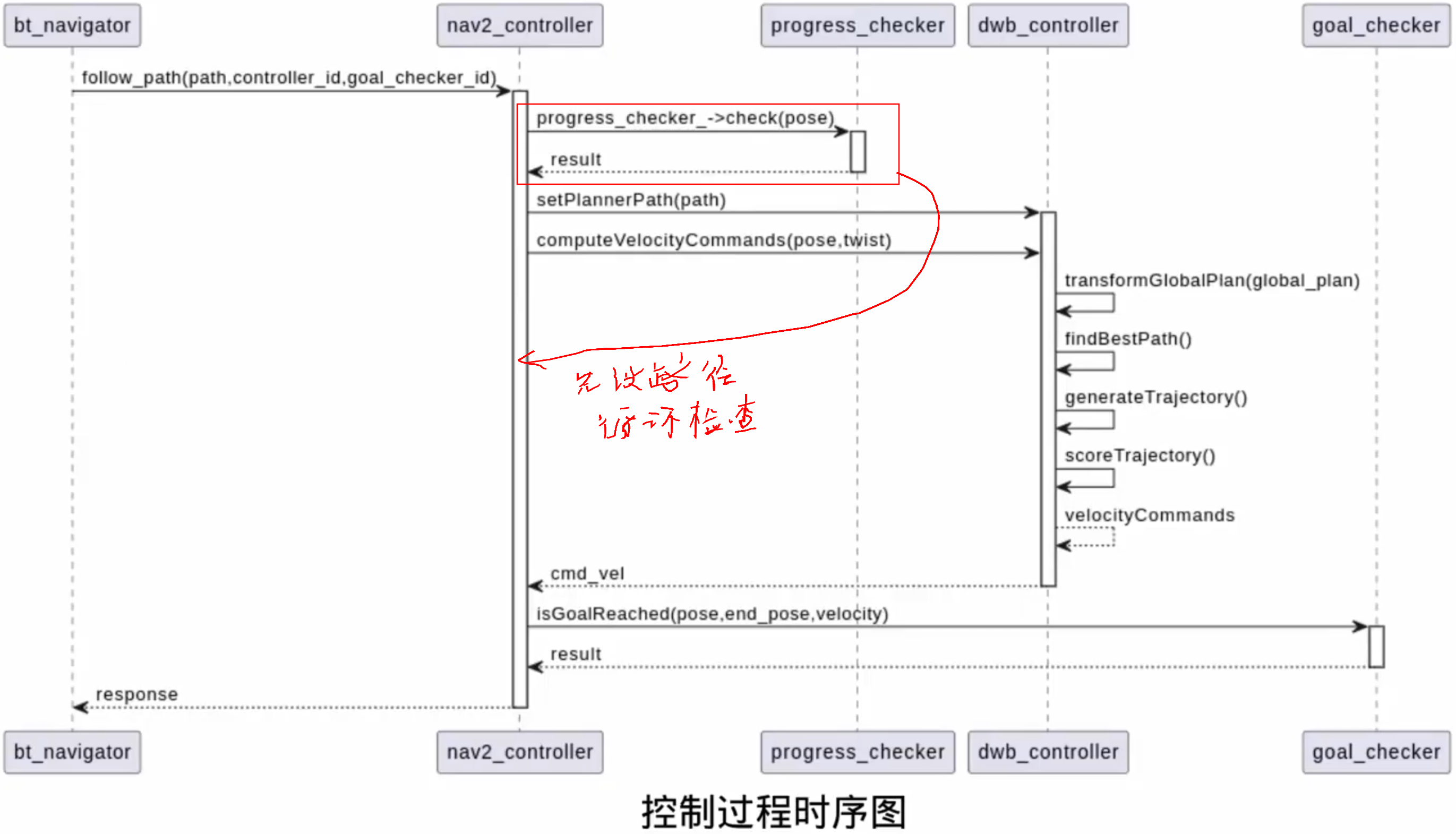
3.开启局部代价地图
和Planner_Server类似
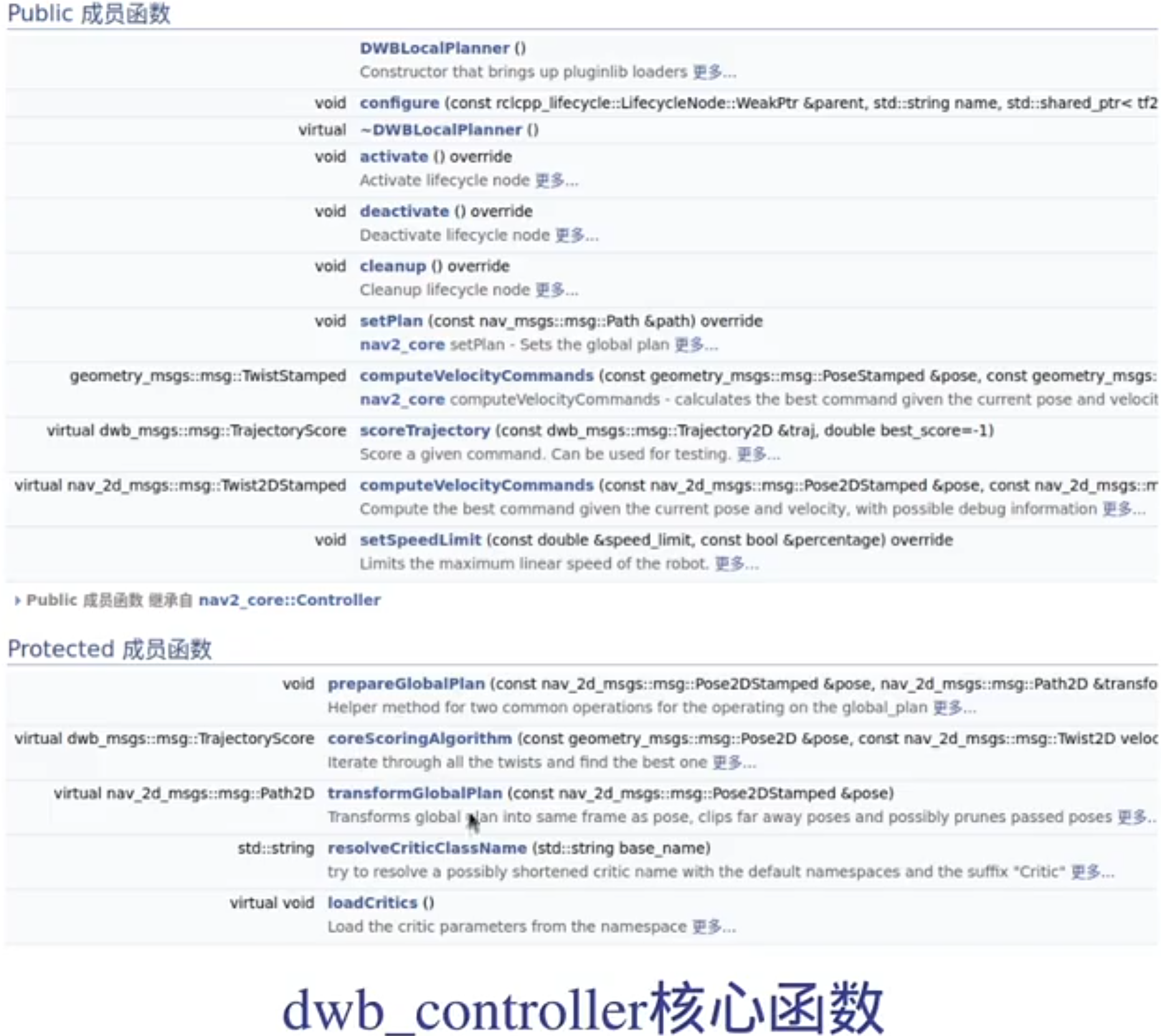
DWB算法详解