图形学

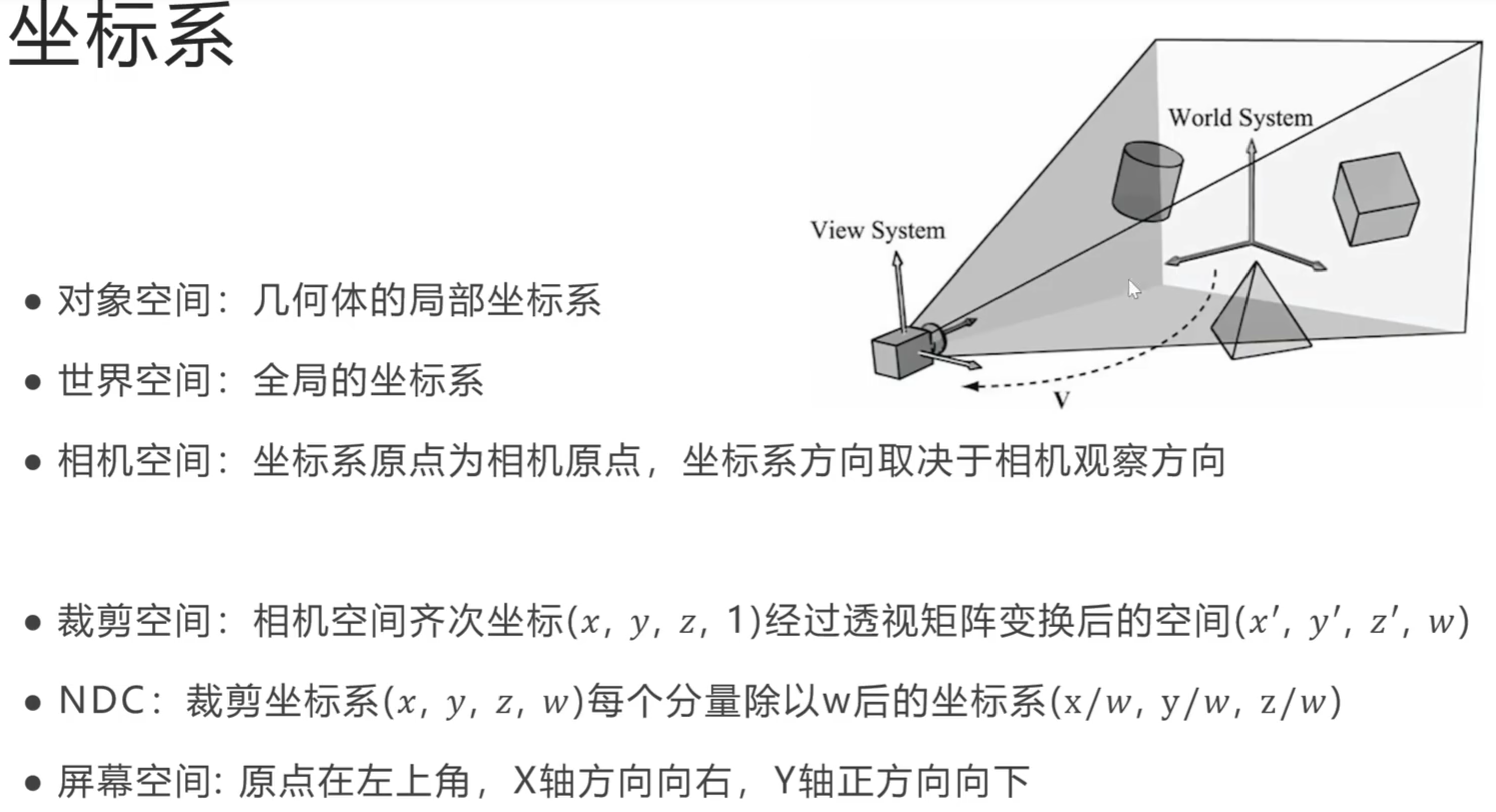
image-20241102163615219

image-20241102170537184

image-20241102170633713

光线与球体的相交测试：

image-20241102170834824

可以通过判断这个一元二次方程的delta判别式判断光线是否击中了球体

结构体：默认的成员访问权限是 public。

类：默认的成员访问权限是 private。

视口裁剪（Viewport Clipping）

视口裁剪是指在渲染过程中，图形系统根据当前的视口（viewport）大小和位置，裁剪出只在视口内的部分。这通常发生在将三维场景转换为二维图像时。

  • 视口定义：视口是指在窗口或屏幕上的一个矩形区域，图形渲染的结果只显示在这个区域内。
  • 用途：视口裁剪确保只绘制视口范围内的图形，避免无效的计算和渲染，提高效率。

透视裁剪（Perspective Clipping）

透视裁剪是指在透视投影过程中，决定哪些对象在视锥体内并且可见，从而只渲染可见部分。透视投影会产生一个视锥体，位于观察者与场景之间。

  • 视锥体：在透视投影中，视锥体是一个从观察点（摄像机位置）向外扩展的锥形区域。只有位于这个区域内的对象才会被渲染。
  • 裁剪：透视裁剪会去除视锥体外的对象，避免不必要的计算和渲染，并处理对象的深度关系。

总结

  • 视口裁剪：关注的是最终图像在屏幕上的显示区域，只显示视口内的内容。
  • 透视裁剪：关注的是三维场景中哪些对象在视锥体内，以决定哪些对象是可见的。

屏幕空间和 NDC（Normalized Device Coordinates）空间之间的关系:

坐标变换流程

在图形渲染过程中，顶点坐标经历多个变换，从世界空间到最终的屏幕空间，这个过程大致包括：

  1. 模型变换：将顶点从局部模型坐标转换到世界坐标。
  2. 视图变换：将世界坐标转换到相机坐标（视图空间）。
  3. 投影变换：将相机坐标转换到裁剪空间。
  4. 裁剪：将不在视野范围内的顶点剔除。
  5. 透视除法：将裁剪空间的坐标转换到 NDC 空间。这个步骤涉及将每个坐标的 x、y 和 z 分别除以 w（齐次坐标），使得坐标范围归一化到 [-1, 1]。

NDC 到屏幕空间的转换

一旦顶点处于 NDC 空间，它们需要被转换到屏幕空间：

  1. 视口变换：将 NDC 坐标映射到实际的屏幕像素坐标。视口变换使用屏幕的分辨率来进行坐标的线性变换。具体步骤是：
    • 将 NDC 的 x 和 y 坐标从 [-1, 1] 范围映射到屏幕像素的范围。例如，对于一个宽度为 W，高度为 H 的屏幕：
      • screenX = (ndcX + 1) * 0.5 * (W - 1)
      • screenY = (1 - (ndcY + 1) * 0.5) * (H - 1)（Y 轴可能需要翻转，具体取决于坐标系统的定义）
  • NDC 空间 是一个归一化的坐标系统，主要用于在渲染管线中的处理，使得顶点坐标能够统一处理，不论目标显示设备的分辨率如何。
  • 屏幕空间 是实际显示的坐标系统，与屏幕的物理尺寸和分辨率相关。
  • 转换：通过视口变换，NDC 空间的坐标被转换为屏幕空间的像素坐标，从而最终呈现在用户的屏幕上。

NDC 空间可以看作是从三维世界到二维屏幕的中间步骤，而屏幕空间则是最终的输出结果。

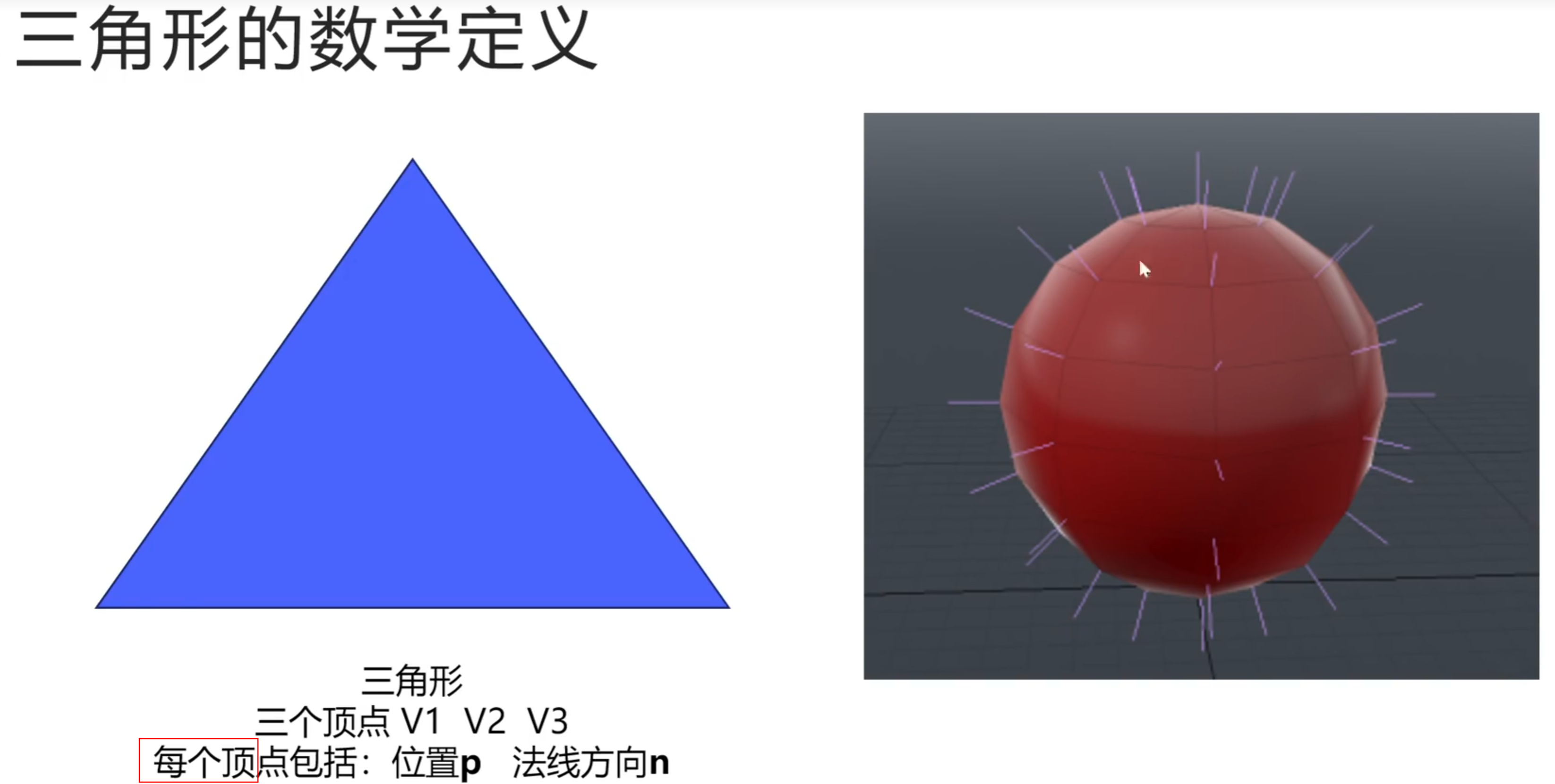
image-20241103175728042

image-20241103181614993

虚函数（Virtual Function）

  1. 定义：虚函数是在基类中声明为virtual的成员函数，可以在派生类中重写（override）。
  2. 实现：虚函数可以有具体的实现。基类中的虚函数可以提供默认的实现，派生类可以选择重写它。
  3. 对象创建：可以创建基类的对象，也可以创建派生类的对象。

纯虚函数（Pure Virtual Function）

  1. 定义：纯虚函数是在基类中声明为virtual并且等于0的函数。语法是virtual void functionName() = 0;。
  2. 实现：纯虚函数没有实现，基类通常不可以实例化。
  3. 对象创建：不能直接创建类的对象（即抽象类），只能创建派生类的对象。
  4. 用途：用于定义接口，强制派生类实现特定的函数

输入流操作符 (>>) 在处理流时，会自动跳过空格和其他空白字符（如换行符和制表符），直到遇到下一个有意义的值为止。因此，空格在这一过程中并不会被显式处理。

line.compare(0, 2, "v ") 的含义：

  1. **0**：表示从 line 字符串的第一个字符开始进行比较。
  2. **2**：表示比较的长度为 2，也就是说，只比较 line 字符串的前两个字符。
  3. **"v "**：表示要将 line 字符串的前两个字符与字符串 "v " 进行比较。
  4. 如果 line 的前两个字符与 "v " 完全匹配，compare 方法返回 0。
  5. 如果不匹配，返回一个非 0 的值（具体的值取决于比较的结果：如果 line 字符串小于 "v "，返回一个负数；如果 line 字符串大于 "v "，返回一个正数）。

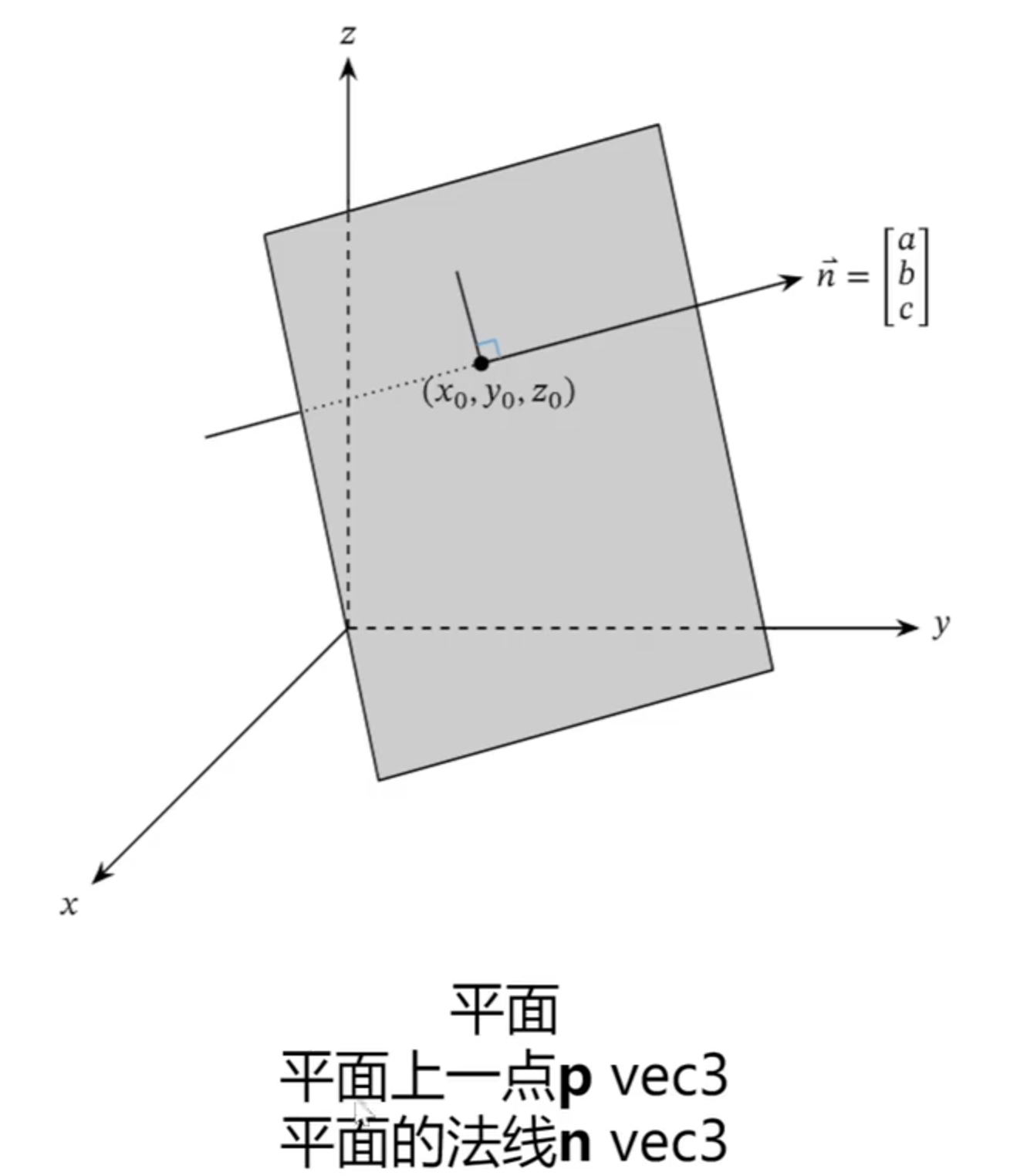
平面和场景

场景：管理世界空间下所有的形状（Shape）

平面的数学定义：

image-20241105220133619

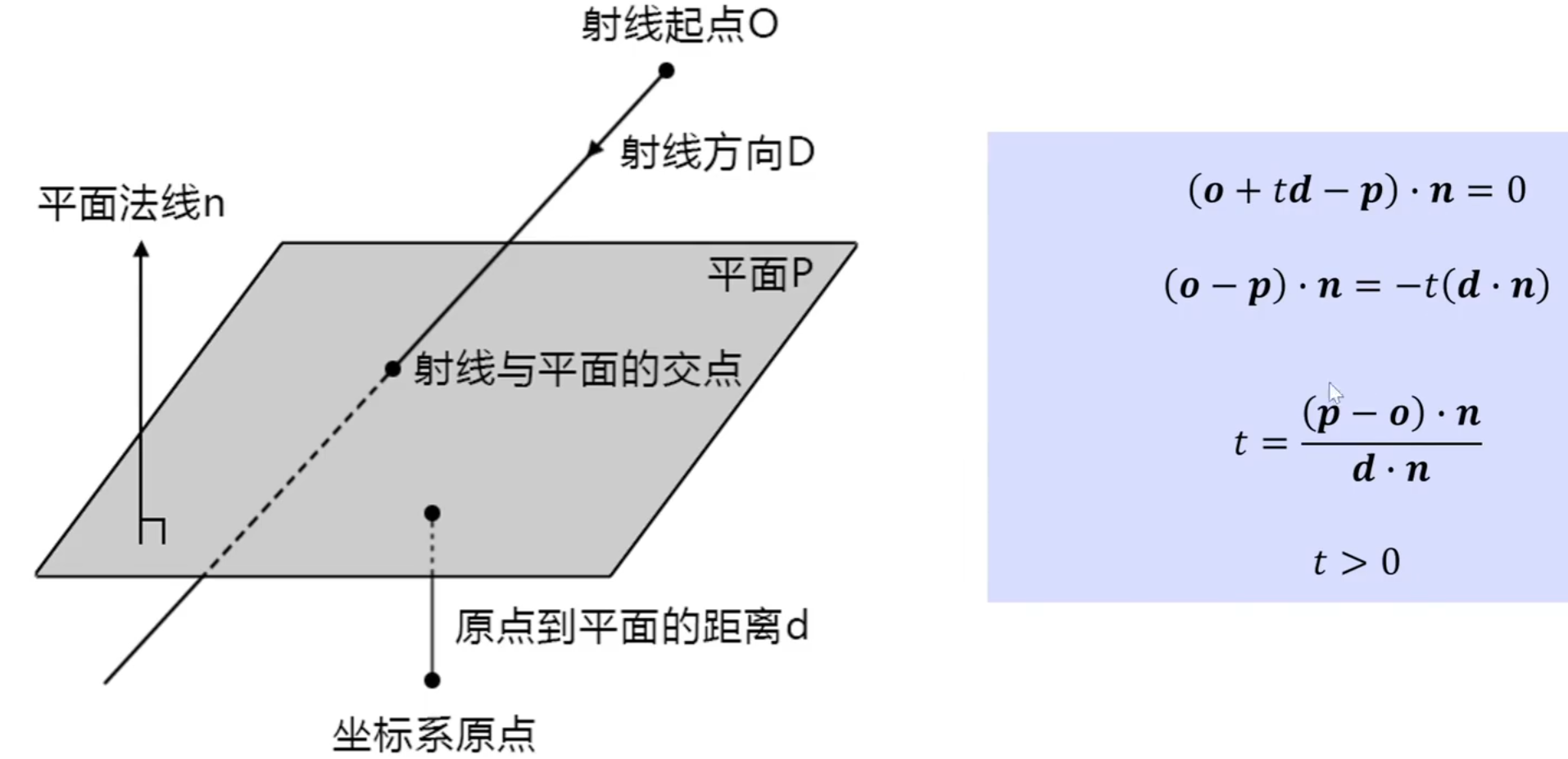
image-20241105220823204

修改是为了改进多线程环境中的 线程安全性 和 竞态条件 的问题。我们来详细分析一下原始代码和修改后的代码之间的差异，以及为什么要这样修改。

原始代码：

count++; 
if (count % film.getWidth() == 0) {
    std::cout << static_cast<float>(count) / (film.getWidth() * film.getHeight()) << std::endl;
}

修改后的代码：

int n = ++count;
if (n % film.getWidth() == 0) {
    std::cout << static_cast<float>(n) / (film.getWidth() * film.getHeight()) << std::endl;
}

问题分析：

1. count++ 是非原子操作

  • count++ 实际上是由 两个操作 组成的：读取 count 的值，然后 **增加 count**。在多线程环境中，如果多个线程同时执行 count++，就会发生 竞态条件（race condition），可能导致 count 的值增加不正确或者丢失。
  • 例如，如果线程 A 和线程 B 同时读取到相同的 count 值，然后都加 1 写回，这样就会丢失一个递增的结果，导致 count 的值不准确。

2. ++count 是原子操作

  • ++count 是 自增并返回自增后的值，它在执行过程中是原子的，不会有并发冲突（前提是 count 本身是原子变量或操作）。这是因为它在自增的时候直接对 count 的值进行更新并返回，而不需要先读取再写入，避免了多个线程同时读取和写入的情况。

3. 存储递增结果到 n

  • 修改后的代码 int n = ++count; 将自增后的结果保存在 n 中。这样做的好处是：
    1. 保证了 count 更新后的值在后续代码中是确定的。如果我们直接在 if (count % film.getWidth() == 0) 中访问 count，其他线程可能会在我们检查 count 时修改它，导致判断条件不稳定。而 n 是在更新后的值保存时就固定了，因此后续的判断和输出使用 n 可以确保一致性。
    2. 避免了 count 被其他线程修改时的影响。虽然 count 本身是全局共享的，但通过把递增结果保存在 n 中，我们保证了 n 的值不会在后续代码执行时被其他线程改动，确保了输出的正确性。

线程安全与性能考虑：

  • 使用 int n = ++count; 的修改，确保了 每个线程对 count 的更新是安全的。同时，虽然 ++count 在某些情况下可能是原子操作，但若 count 是一个普通变量，并且没有显式的线程同步机制，那么可能仍然存在隐性的问题。将更新后的 count 值保存到 n 可以减少这种不确定性。
  • 在多线程环境下，避免直接在条件判断中使用共享变量（如 count）是一个常见的做法，尤其是当这个变量在多个线程中共享且没有其他同步机制时。通过中间变量 n 来持有更新后的值，避免了在 count 被其他线程修改时产生的竞态条件。
        glm::translate(glm::mat4(1.f), pos) *
        glm::rotate(glm::mat4(1.f), glm::radians(rotate.z), { 0, 0, 1 }) *
        glm::rotate(glm::mat4(1.f), glm::radians(rotate.y), { 0, 1, 0 }) *
        glm::rotate(glm::mat4(1.f), glm::radians(rotate.x), { 1, 0, 0 }) *
        glm::scale(glm::mat4(1.f), scale)
  • glm::mat4(1.f)：创建一个单位矩阵，表示没有任何变换。
  • glm::translate(..., pos)：将矩阵平移到 pos 指定的位置，pos 是一个 glm::vec3 向量,表示物体在3D空间中的平移偏移量（x, y, z）。
  • glm::radians(rotate.z)：将角度 rotate.z 转换为弧度，因为GLM的 rotate 函数期望的旋转角度单位是弧度。
  • { 0, 0, 1 }：指定旋转轴为Z轴。
  • glm::scale(glm::mat4(1.f), scale)：执行一个缩放变换，其中 scale 是一个 glm::vec3 向量，表示沿着X、Y和Z轴的缩放比例。例如，scale = { 2.f, 3.f, 1.f } 表示在X轴上放大2倍，在Y轴上放大3倍，而Z轴保持不变。

在GLM中，矩阵的乘法是从 右到左 进行的

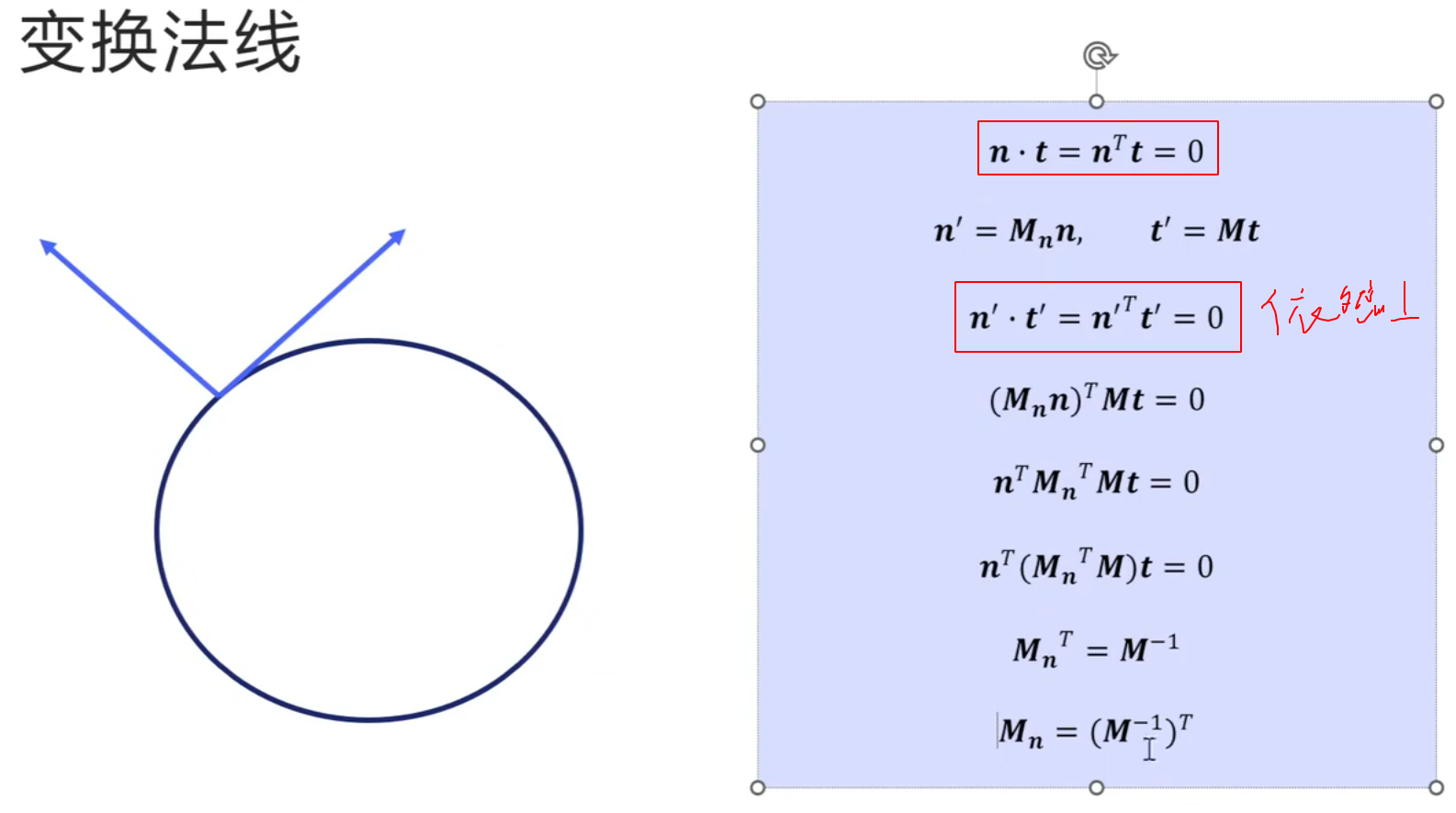
image-20241109162036809

image-20241109213953208

image-20241110094231486

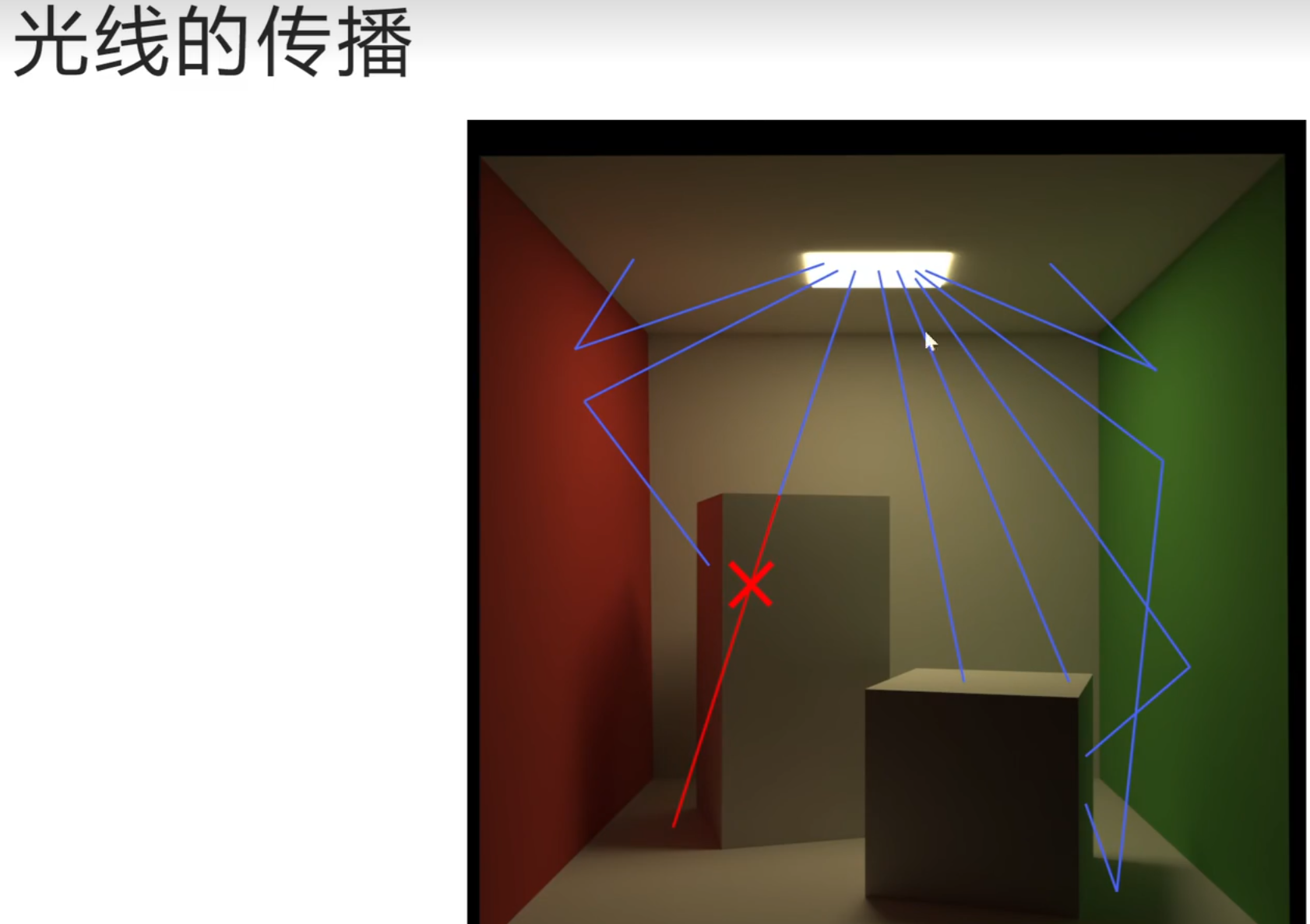
image-20241110095142061

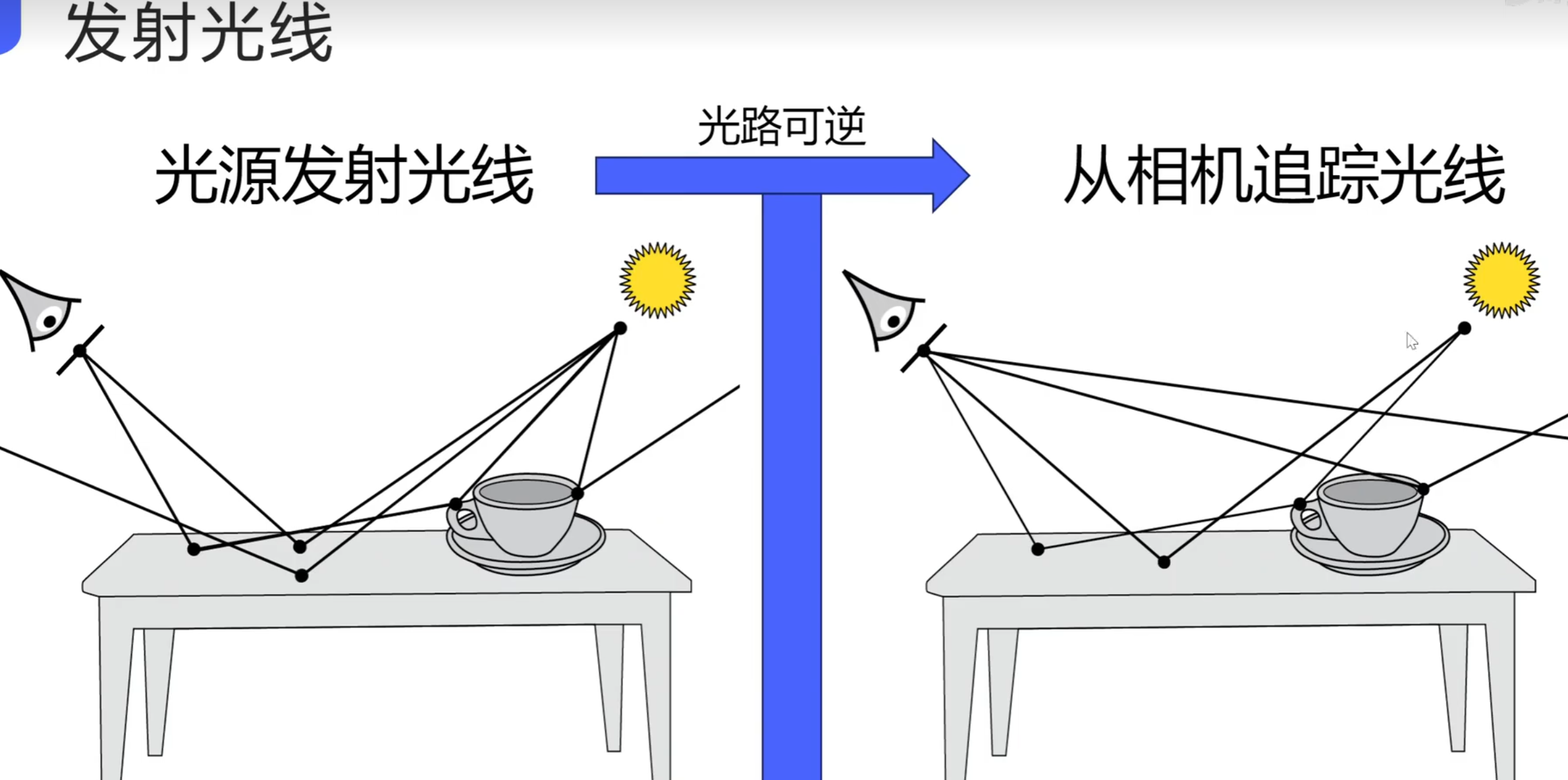
image-20241110095414276

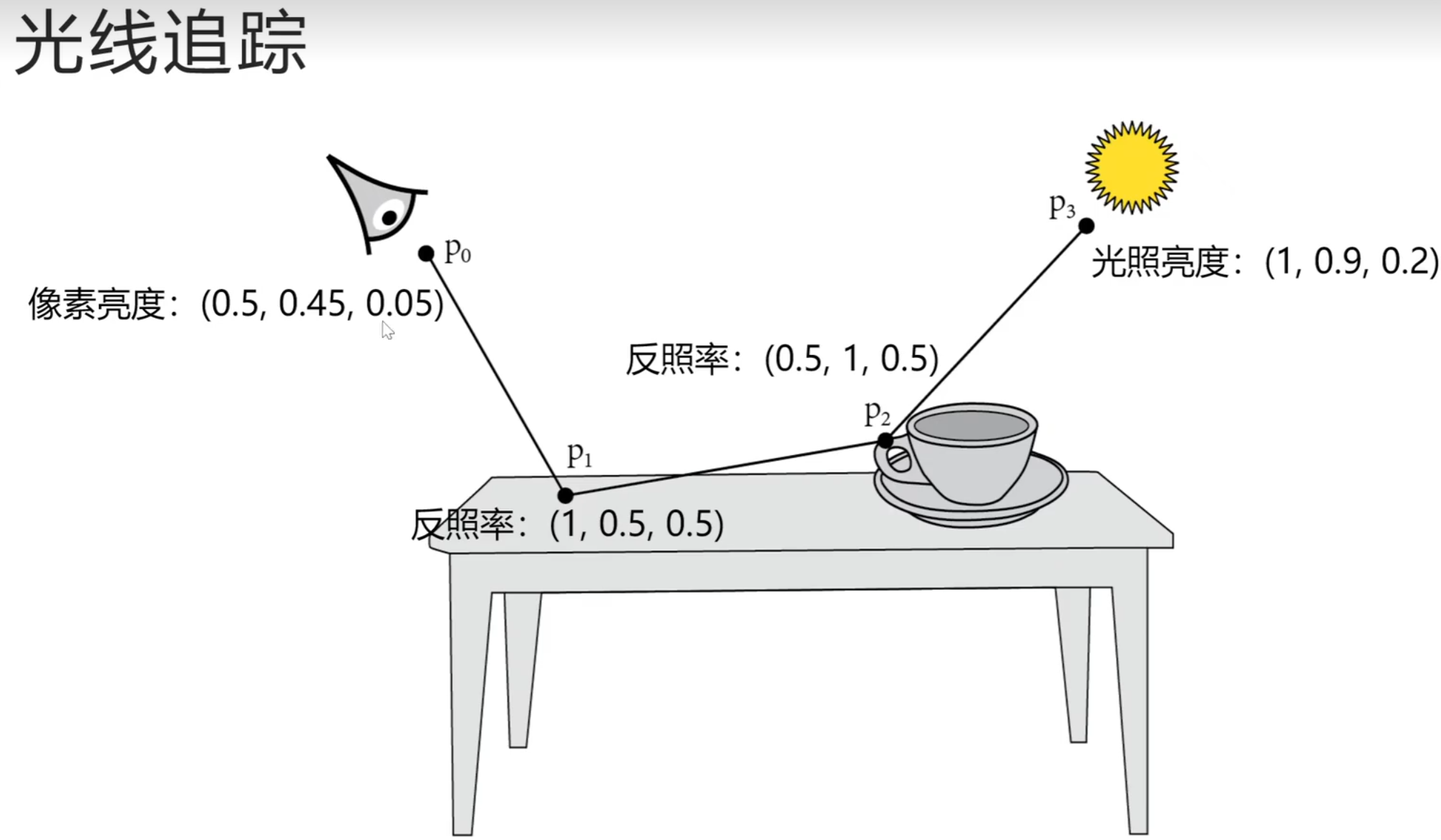
image-20241110095522416

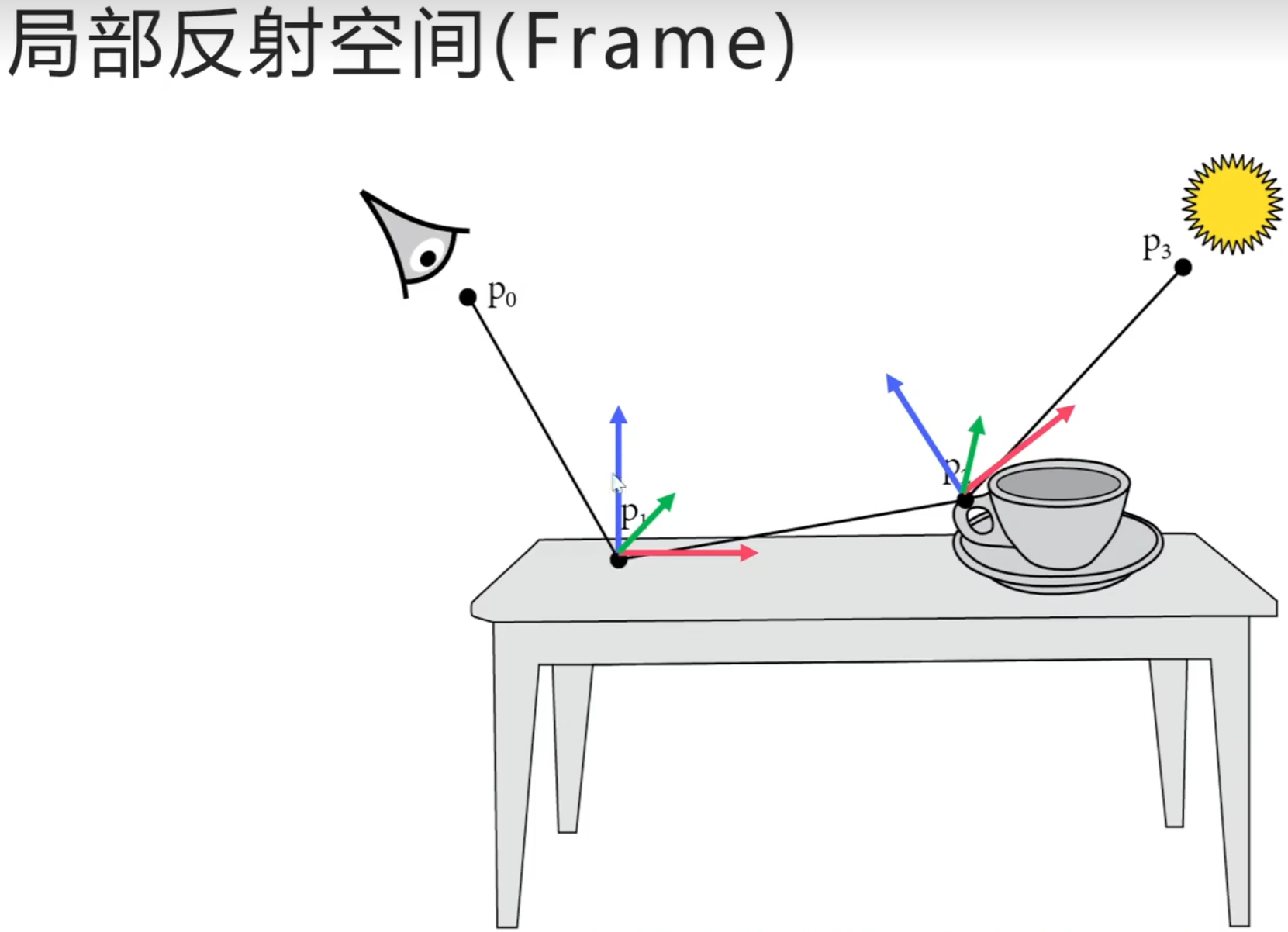
image-20241110144226840

frame坐标系不用储存坐标系的原点，只用存储坐标轴的方向

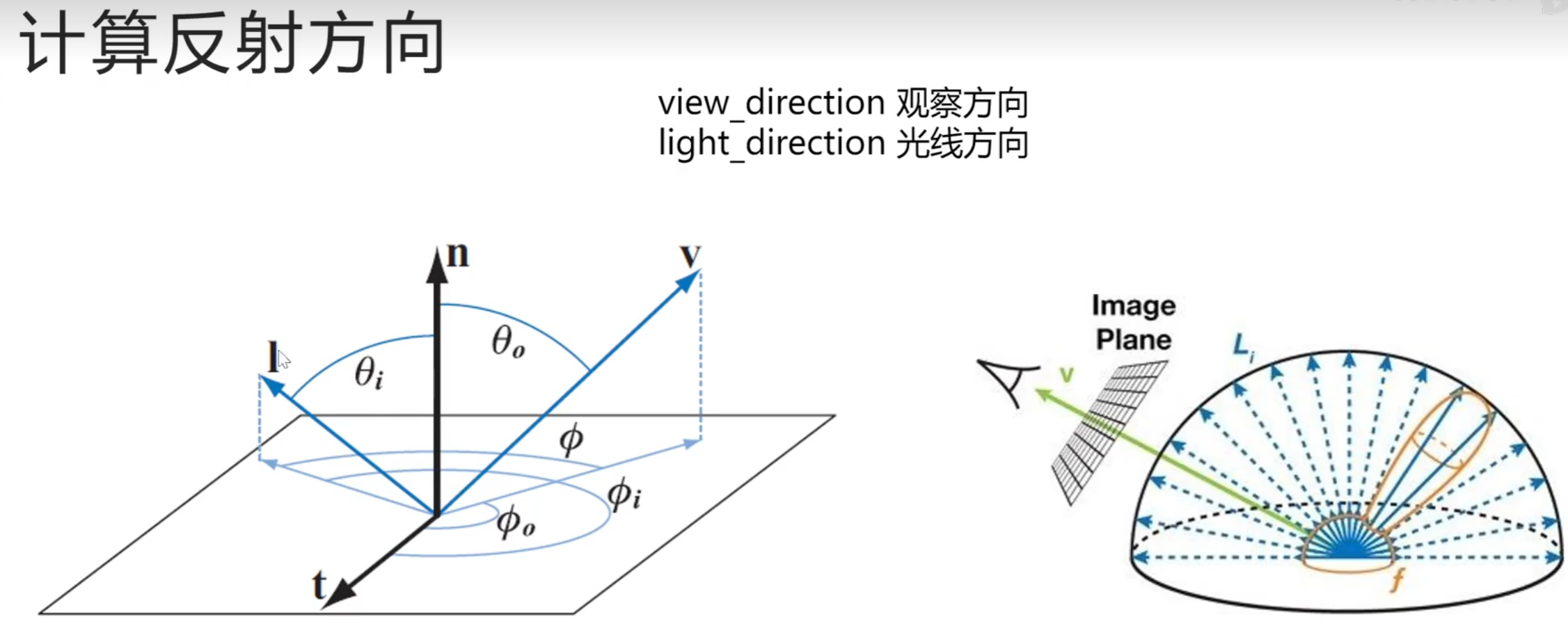
image-20241112092245780

镜面反射：x,z取反

漫反射：采样

image-20241112092430966

for (size_t i = 0; i < shapeInstances.size(); i++) {
    auto shapeInstance = shapeInstances[i];
    auto ray_object = ray.rayObjectFromWorld(shapeInstance.object_from_world);
    hitInfo = shapeInstance.shape.intersect(ray_object, t_min, t_max); // 需要把世界空间下的光线转换成对象空间里相交测试
    if (hitInfo.has_value()) {
        t_max = hitInfo->distance;
        closest_hitInfo = hitInfo;
        closest_instance = &shapeInstance;
    }
}

与：

    for (size_t i = 0; i < shapeInstances.size(); i++) {
        auto ray_object = ray.rayObjectFromWorld(shapeInstances[i].object_from_world);
        hitInfo = shapeInstances[i].shape.intersect(ray_object, t_min, t_max); //需要把世界空间下的光线转换成对象空间里相交测试
        if (hitInfo.has_value()) {
            t_max = hitInfo->distance;
            closest_hitInfo = hitInfo;
            closest_instance = &shapeInstances[i];
        }
    }

看似一样，实则不一样

第一个是拷贝，

shapeInstance 就是一个独立的对象，它与原始 shapeInstances[i] 没有直接关系

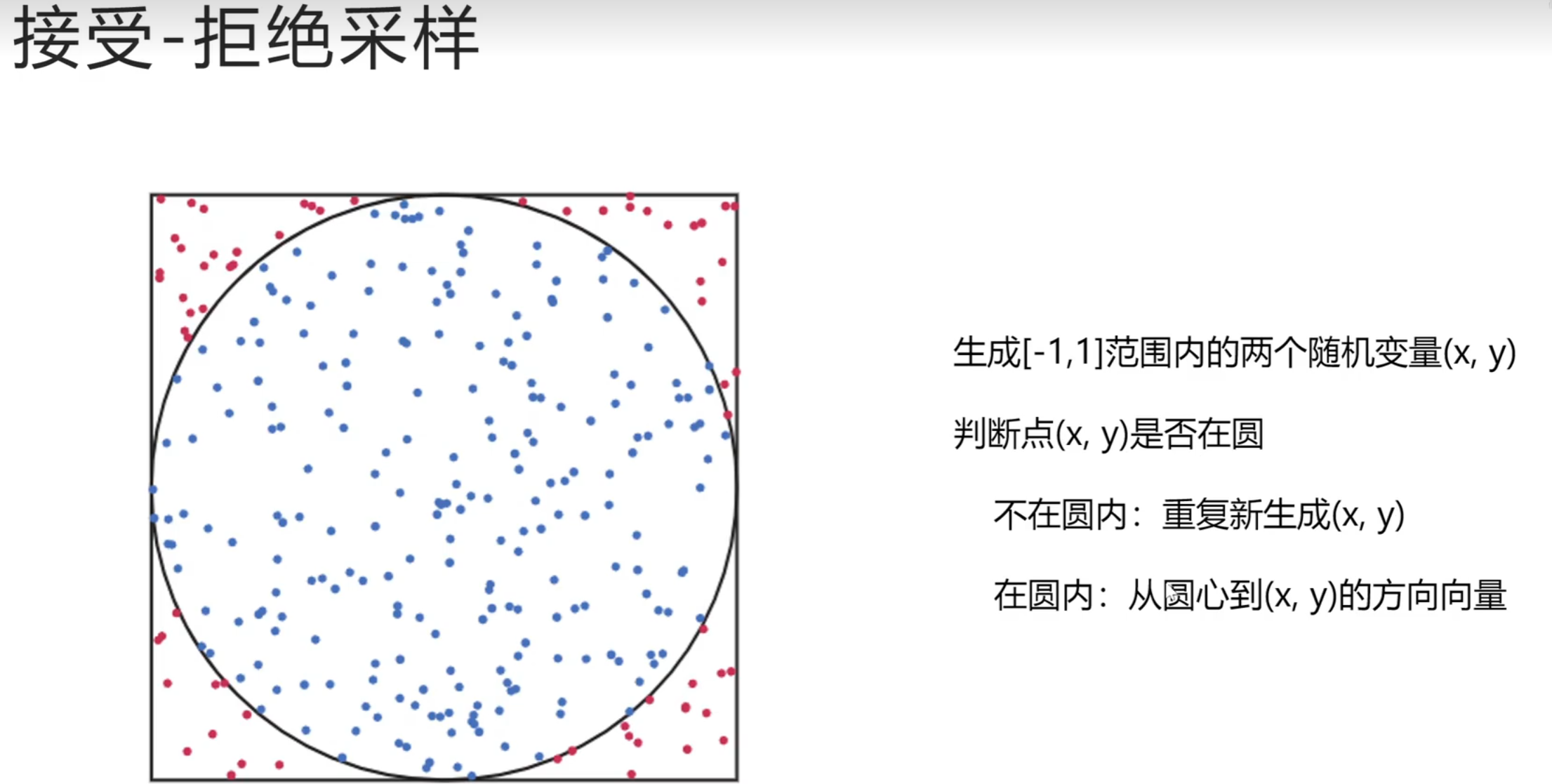
减小光追的噪点：

image-20241112200209893