2025-01-16

kitty

2025-01-09

guitar

2024-12-10

最优控制与强化学习

2024-12-03

ncnn-yolov8-seg

yoloV8-segment模型安卓端部署

注：开发环境为ubuntu20.04;

ncnn为2022.11.28版本;
opencv-mobile为4.6.0版本;

使用yoloV8n,m,l-seg;

介绍：ncnn是一款非常高效易用的深度学习推理框架，支持各种神经网络模型，如pytorch、tensorflow、onnx等，以及多种硬件后端，如x86、arm、riscv、mips、vulkan等。ncnn 是一个为手机端极致优化的高性能神经网络前向计算框架。 ncnn 从设计之初深刻考虑手机端的部署和使用。无第三方依赖，跨平台，手机端 cpu 的速度快于目前所有已知的开源框架。基于 ncnn，开发者能够将深度学习算法轻松移植到手机端高效执行，开发出人工智能 APP，将 AI 带到你的指尖。 ncnn 目前已在腾讯多款应用中使用，如：QQ，Qzone，微信，天天 P 图等。

一.模型转换：best.pt——>yolov8n-seg.bin和yolov8n-seg.param

(以yolov8n为例)

起初，直接使用ultralytics官方转换，但是转换后的模型导致APP闪退，查看yolov8n-seg.param:

得知：里面有很多的MemoryData，不够干净。
于是模型转换step by step:

1. build ncnn

1. sudo apt install cmake protobuf-compiler libprotobuf-dev libopencv-dev
2, gitclone https://github.com/Tencent/ncnn/releases
3, 编译 NCNN
cd ncnn-master
mkdir build
cd build
cmake ..
make
make install
得到了onnx2ncnn转换工具

2. convert yolov8 pt ->ONNX

from ultralytics import YOLO

# load yolov8 segment model
model = YOLO("your_path")
# concert the model
success = model.export(format="onnx", opset=12, simplify=True)

3. onnx2ncnn

ONNX介绍

ONNX是一种针对机器学习所设计的开放式的文件格式，用于存储训练好的模型。它使得不同的深度学习框架（如Pytorch, MXNet）可以采用相同格式存储模型数据。是一种便于在各个主流深度学习框架中迁移模型的中间表达格式。

onnx2ncnn xxx.onnx xxx.param xxx.bin

在这里xxx.param 存储了模型的参数信息，它记录了计算图的结构。而xxx.bin 则存放了模型的所有具体参数。就可以使用 ncnn 框架来加载和运行这个模型了。

4. 但是也会闪退！！！

分析一下yolov8n-seg.param文件，问题一样，也是存在MemoryData问题和模型缺少permute层的问题,都会导致ncnn框架无法正确解析param模型

坑：需修改ultralytics源码modules文件夹里的block.py和head.py两个文件,修改3个forward函数,改变前向传播的方式：

class C2f(nn.Module):

  def forward(self, x):

    x = self.cv1(x)

    x = [x, x[:, self.c:, ...]]    

    x.extend(m(x[-1]) for m in self.m)

    x.pop(1)

    return self.cv2(torch.cat(x, 1))

class Detect(nn.Module):

  def forward(self, x):

    shape = x[0].shape

    for i in range(self.nl):

      x[i] = torch.cat((self.cv2[i](x[i]), self.cv3[i](x[i])), 1)

    if self.training:

      return x

    elif self.dynamic or self.shape != shape:

      self.anchors, self.strides = (x.transpose(0, 1) for x in make_anchors(x, self.stride, 0.5))

      self.shape = shape

    pred = torch.cat([xi.view(shape[0], self.no, -1) for xi in x], 2)

    return pred

class Segment(Detect):

  def forward(self, x):

    p = self.proto(x[0])  # mask protos

    bs = p.shape[0]  # batch size

 

    mc = torch.cat([self.cv4[i](x[i]).view(bs, self.nm, -1) for i in range(self.nl)], 2)  

    x = self.detect(self, x)

    if self.training:

      return x, mc, p

    return (torch.cat([x, mc], 1).permute(0, 2, 1), p.view(bs, self.nm, -1)) if self.export else (torch.cat([x[0], mc], 1), (x[1], mc, p))

5. 重新执行3，4步操作

二. 模型转换完毕，下面开始使用Android studio构建安卓工程

1. Configure ncnn

Download [ncnn-YYYYMMDD-android-vulkan].（预编译库）（来自腾讯优图实验室的nihui大神的开源力作）

Extract ncnn-YYYYMMDD-android-vulkan.zip into app/src/main/jni folder and change the ncnn_DIR path to yours in app/src/main/jni/CMakeLists.txt.

2. Configure OpenCV

Download opencv-mobile-XYZ-android (安卓opencv库)(这个也是nihui大神的又一开源力作,适合在安卓移动端使用的轻量级opencv版本)

step 1. download opencv-mobile source

wget -q https://github.com/nihui/opencv-mobile/releases/latest/download/opencv-mobile-4.10.0.zip
unzip -q opencv-mobile-4.10.0.zip
cd opencv-mobile-4.10.0

step 2. apply your opencv option changes to options.txt

vim options.txt

step 3. build your opencv package with cmake

mkdir -p build
cd build
cmake -DCMAKE_INSTALL_PREFIX=install \
  -DCMAKE_BUILD_TYPE=Release \
  `cat ../options.txt` \
  -DBUILD_opencv_world=OFF ..
make -j4
make install

Extract opencv-mobile-XYZ-android.zip into app/src/main/jni and change the OpenCV_DIR path to yours in app/src/main/jni/CMakeLists.txt.

3. Android studio构建

使用NDK26.1，java

项目目录构成：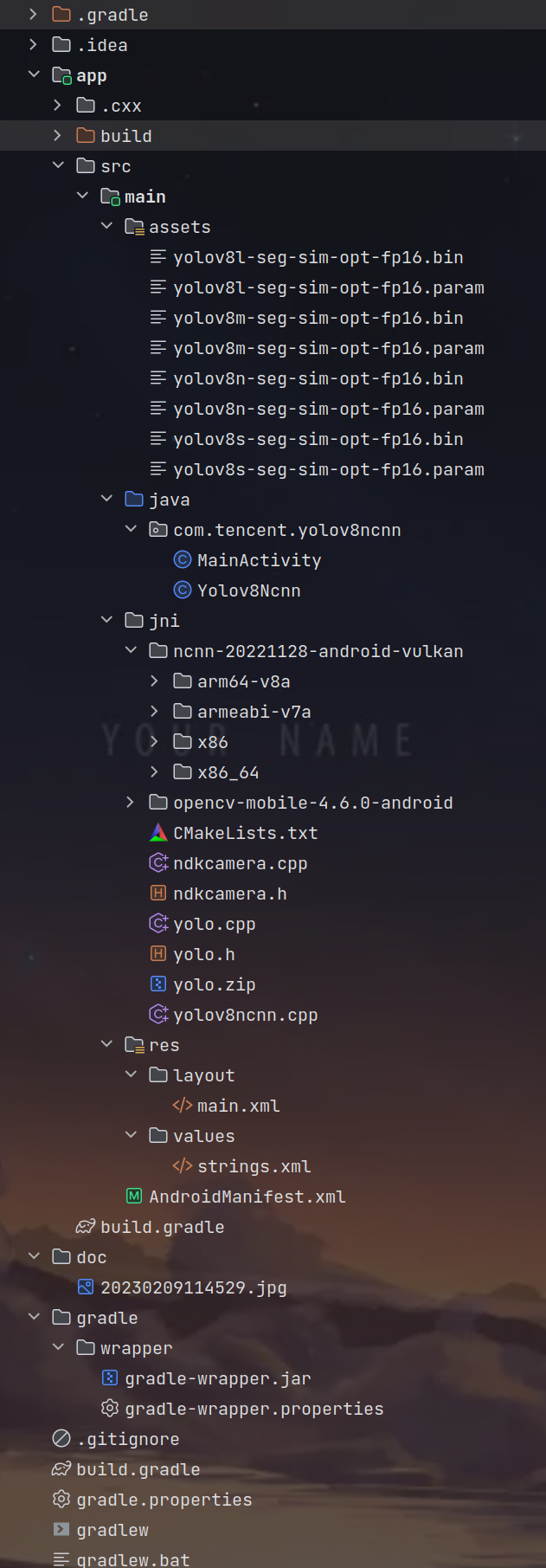

三、构建，烧录

打开安卓设备（本人使用小米,CPU为骁龙8Gen1）开发者选项，USB调试，安装选项，烧录：

效果：

n:

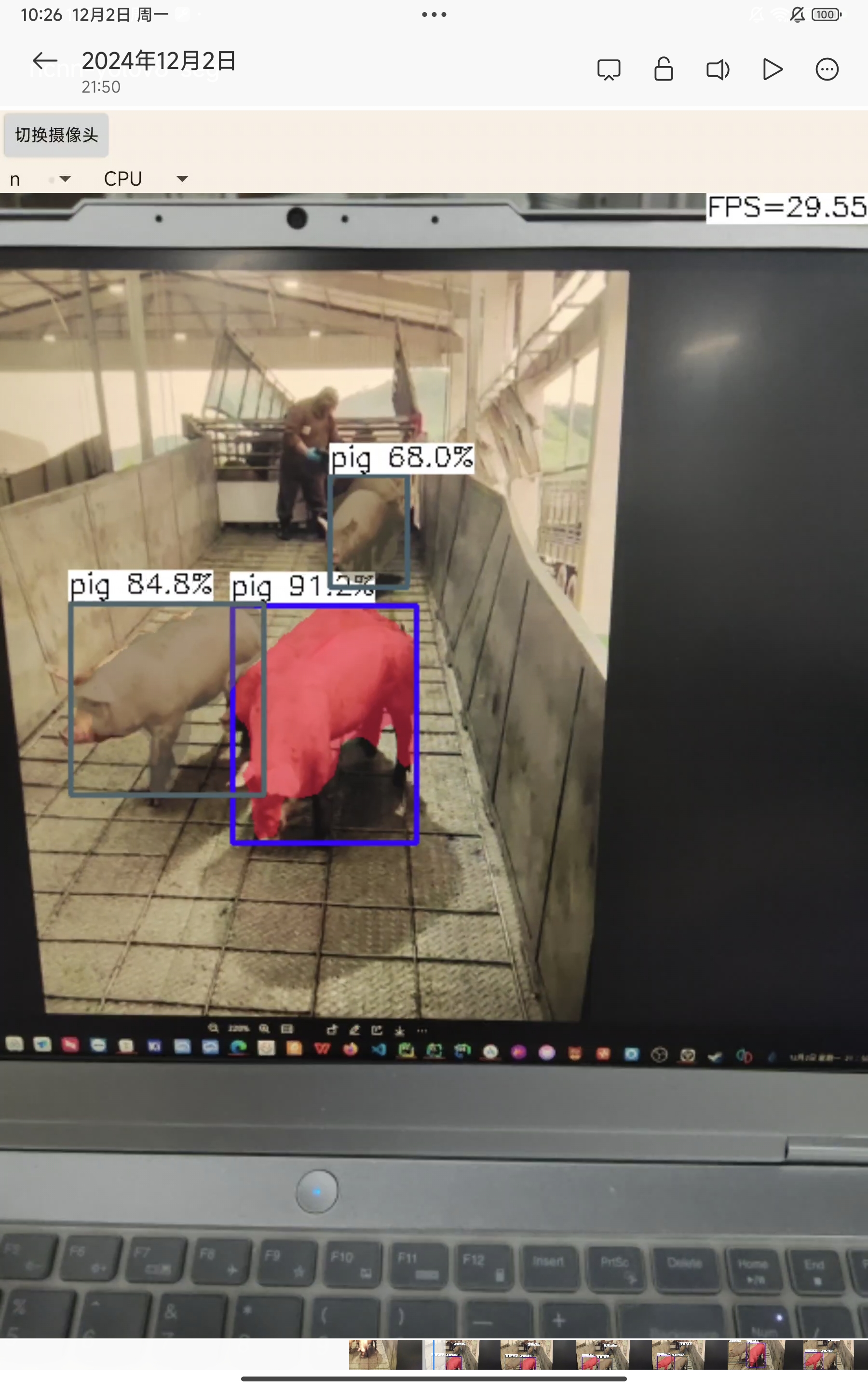
m:

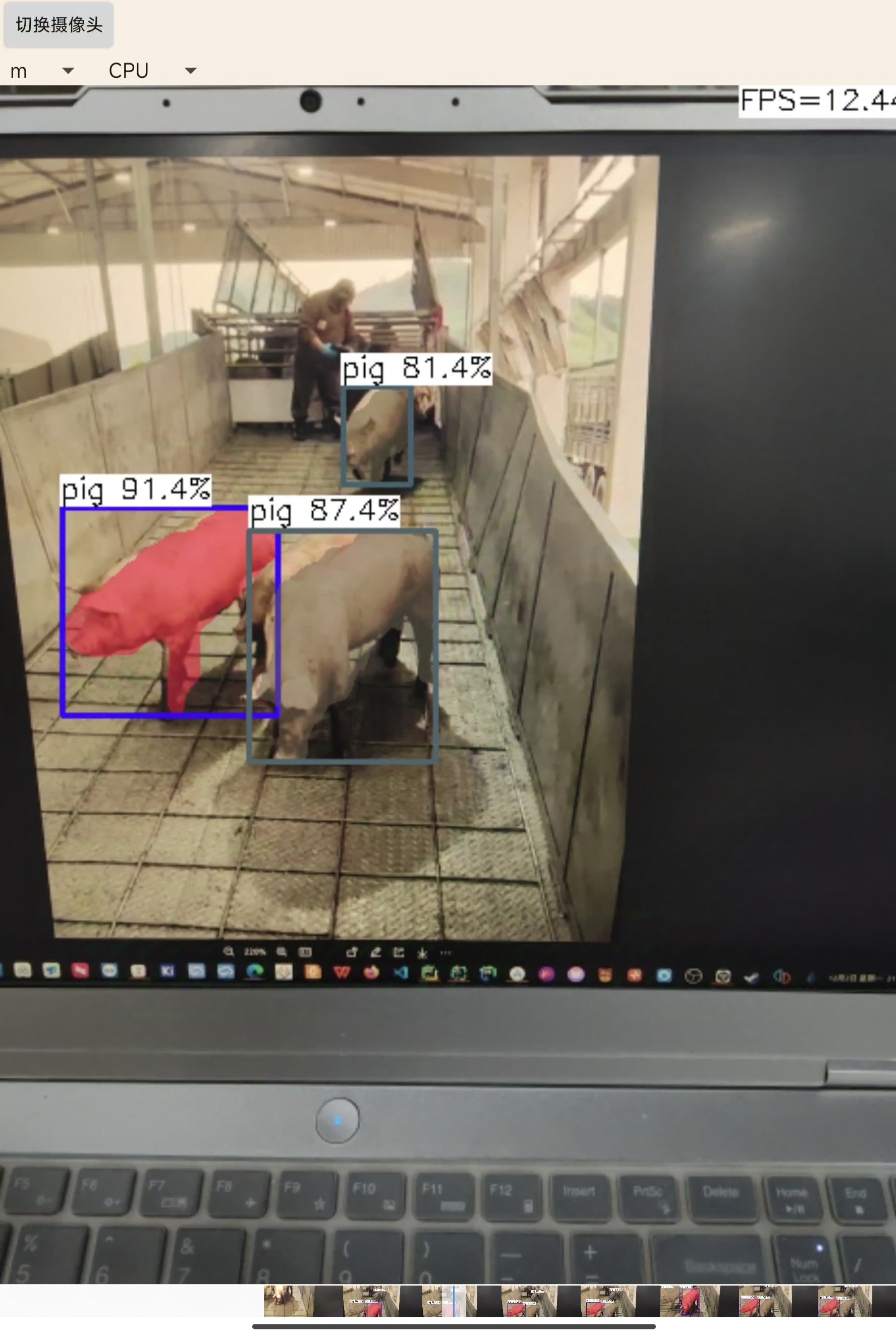
l:

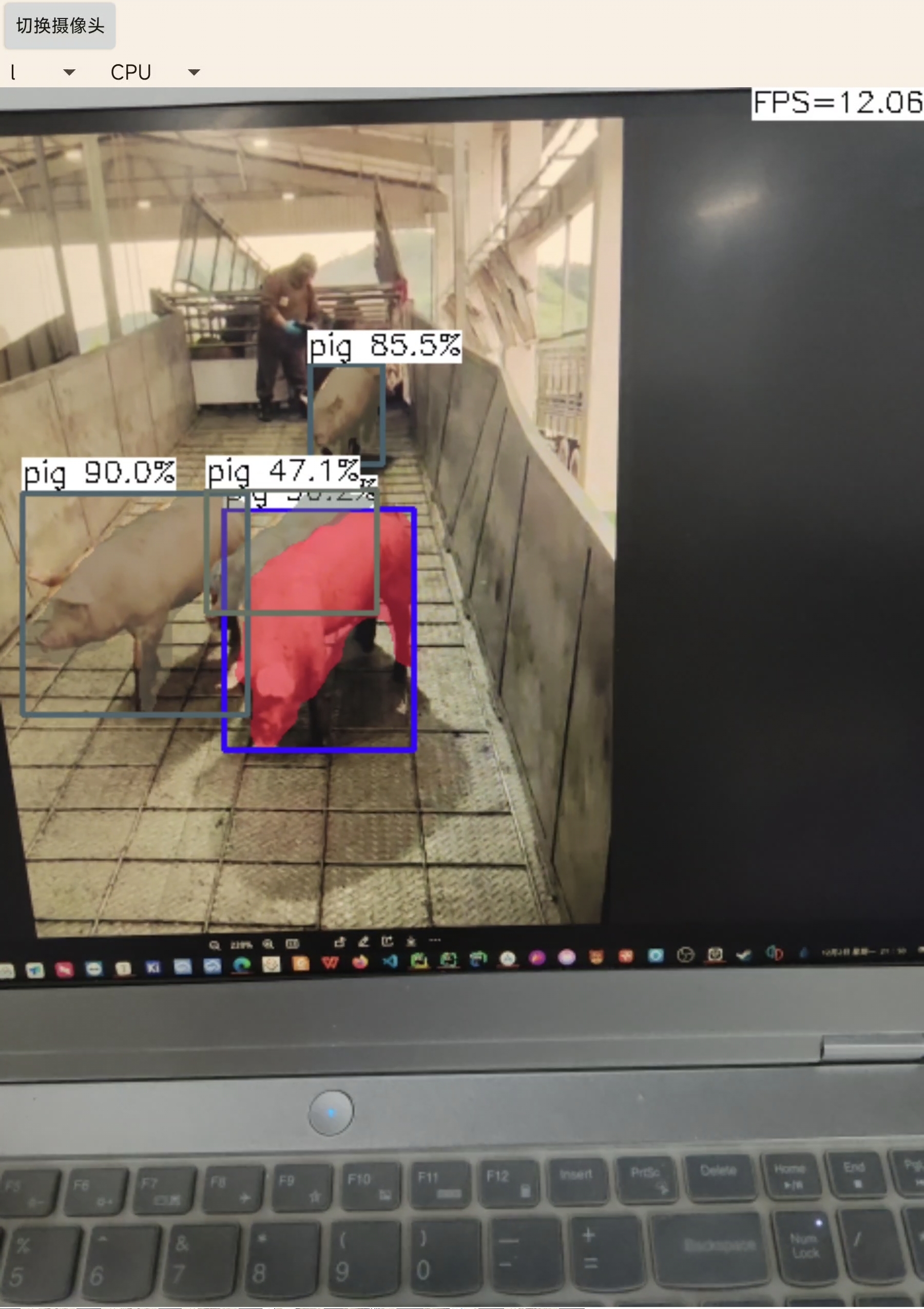
可切换前后摄像头，可切换CPU/GPU

结果分析：

n:帧率在30帧左右，有时会检测不准确，无法将两个挨得较近的识别目标分开

m:帧率在12帧左右，准确性进一步提高

l: 帧率在10帧左右，较为准确，可将挨得较近的识别目标分开

四、模型量化

我们常说的模型量化就是将浮点存储（运算）转换为整型存储（运算）的一种模型压缩技术。比如：原来表示一个权重或偏置需要使用FP32表示，使用了INT8量化后只需要使用一个INT8来表示就可以了。

合并bn层

./ncnnoptimize xxx.param xxx.bin xxx_opt.param xxx_opt.bin 0

生成量化图像集

1.下载校准数据集
git clone https://github.com/nihui/imagenet-sample-images

2.生成量化图像集
find images/ -type f > imagelist.txt  

3.生成量化表
./ncnn2table xxx-opt.param xxx-opt.bin imagelist.txt yolov8-seg.table mean=[104,117,123] norm=[0.017,0.017,0.017] shape=[256,256,3] pixel=BGR thread=8 method=kl

int8 量化

./ncnn2int8 xxx.param xxx.bin xxx_int8.param xxx_int8.bin yolov8-seg.table

把生成的量化后的bin和param替换掉之前的模型，

重新执行第三步即可

效果：

n:

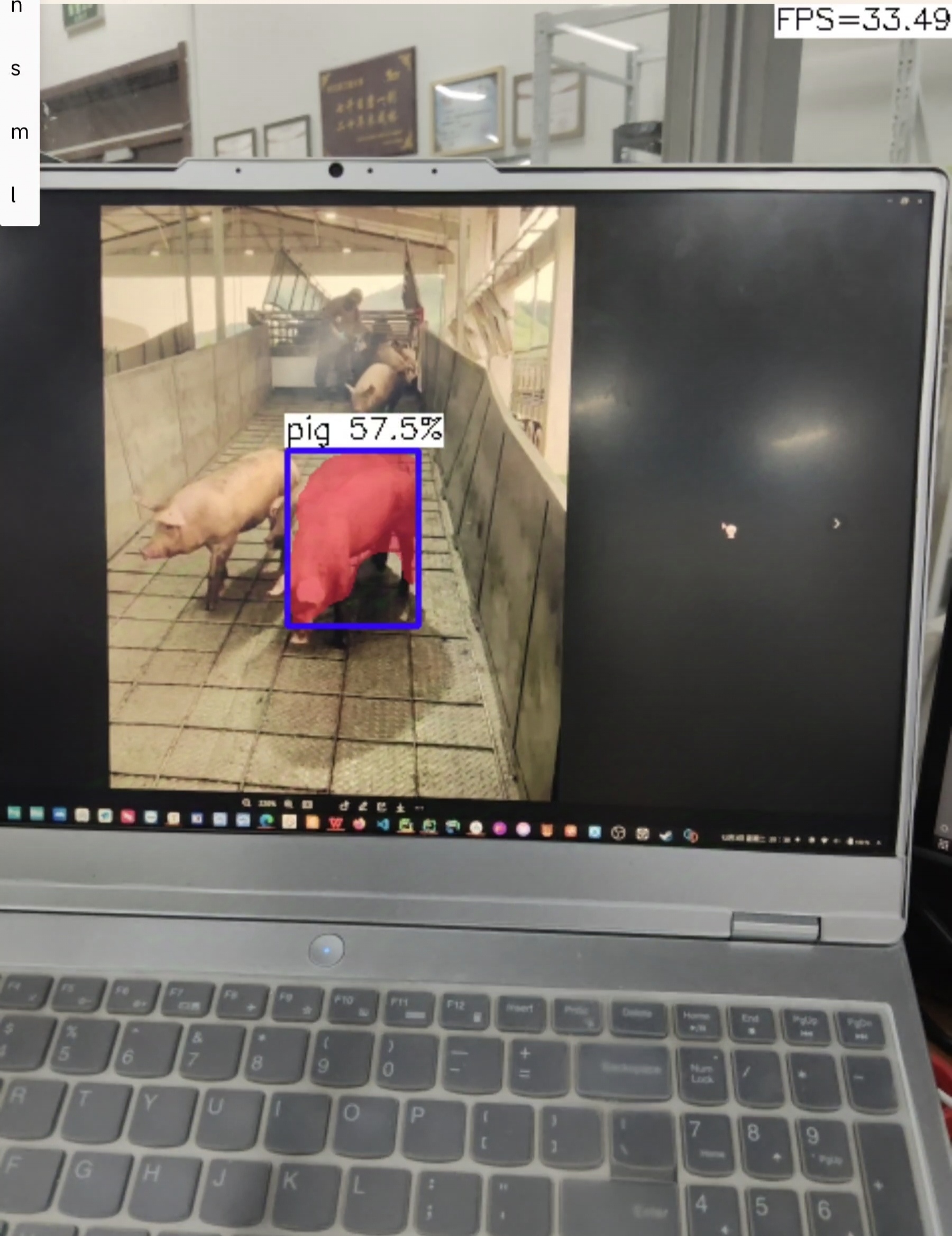
m:

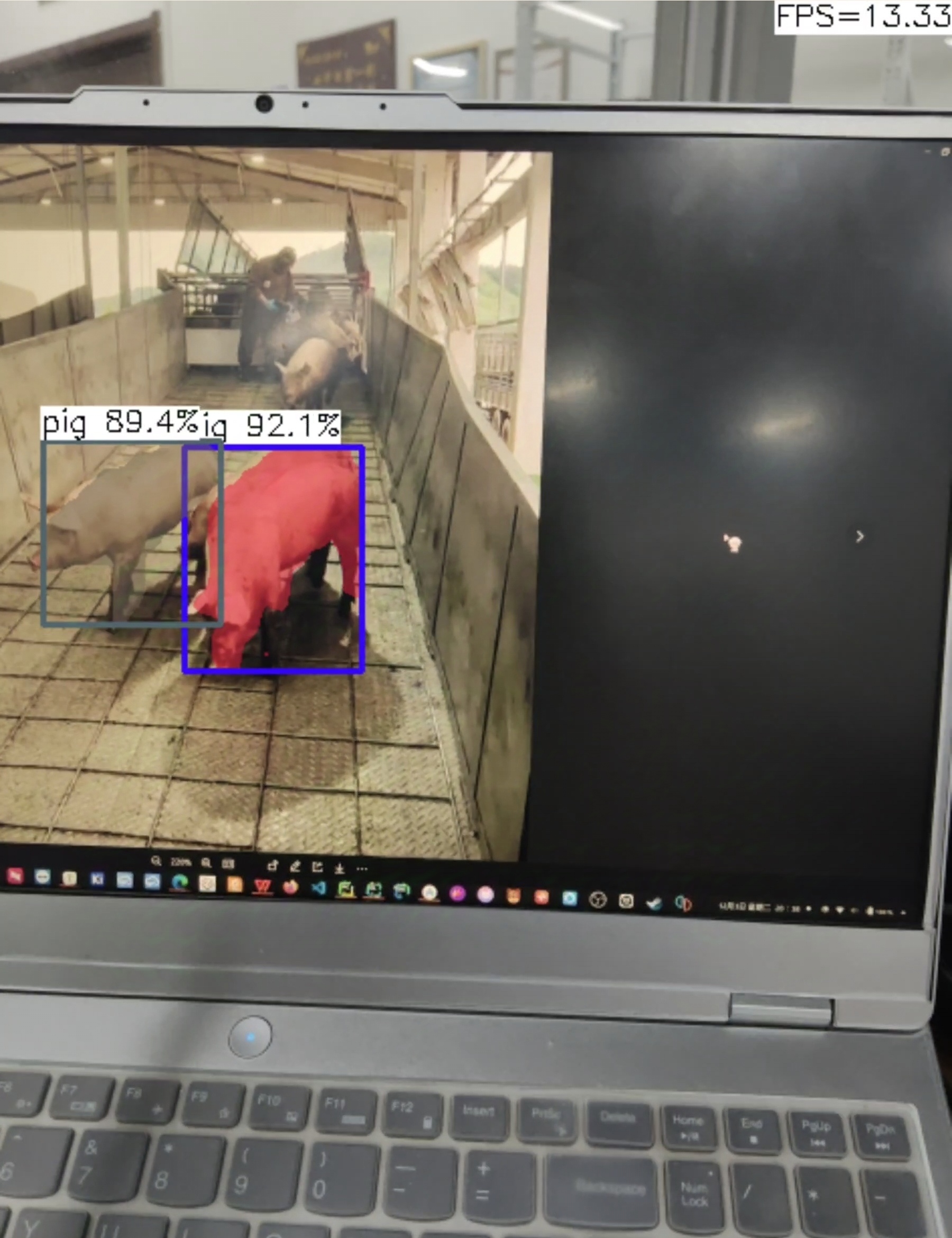
l:

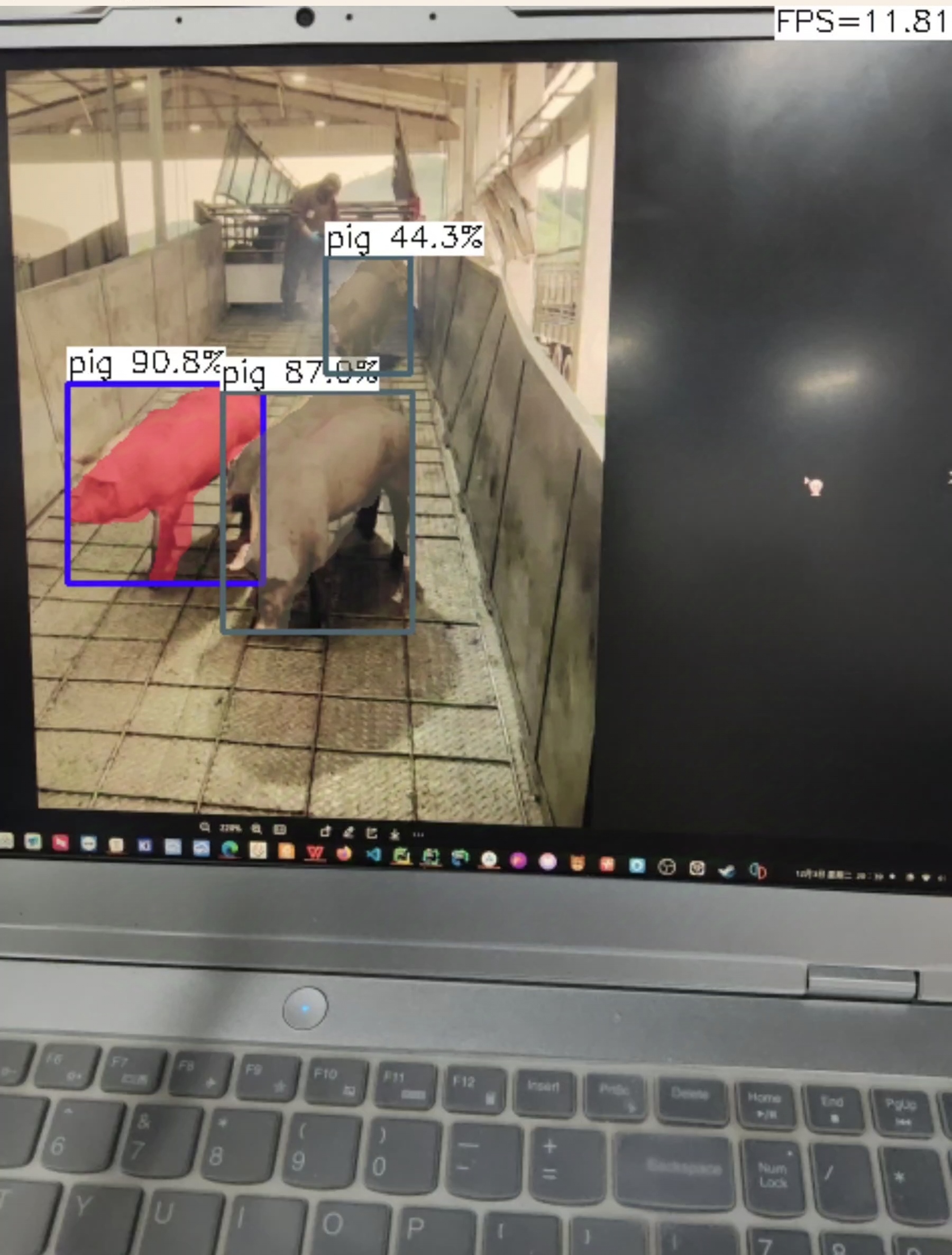
结果分析：

n:帧率提升到34帧左右，检测不太准确，会漏检

m:帧率提升到14帧左右，准确性有些下降，

l: 帧率提升到12帧左右，且准确度下降但不多

完毕！！

2024-12-03

流体力学

质点导数

能量方程

第二粘性系数

将三大守恒控制方程列在一起组成N-S方程

伯努利方程

雷诺平均方程

雷诺应力

雷诺平均方程

脉动方程:

边界层的基本概念中的名义厚度，排挤厚度和动量损失厚度是什么

在流体力学中，边界层是指流体流动中，紧邻固体表面的一层流体区域。该区域内，由于黏性作用，流体的速度从零（在固体表面）逐渐过渡到自由流速度。边界层是流体动力学中的重要概念，它在流体流动、热交换、摩擦力以及流体与固体表面相互作用等方面起着关键作用。

边界层的基本特征主要涉及以下方面：

速度分布：流体速度从零逐渐增大至自由流速度。
边界层厚度：随着流动距离增加，边界层厚度逐渐增大。
流动类型：可以是层流边界层，也可以是湍流边界层。
动量和热量传输：边界层内通过粘性效应和湍流传递动量和热量。
摩擦力：边界层内的黏性摩擦力决定了流体与固体表面之间的摩擦阻力。
边界层分离：在某些条件下，边界层可能会分离，导致流体与表面的失去附着。

3.2

脉动方程

雷诺应力输运方程

层流边界层方程

湍流边界层方程

层流边界层的Blasius解

4.2

雷诺数：

壁面率

对数率

速度亏损率

推导平板混合边界层的摩擦阻力计算公式

5.1

粘性流体涡量输运方程

涡旋运动基本定理中的开尔文定理,拉格朗日涡保持性定理,亥姆霍兹涡线和涡管保持性定理是什么

题

5.2

给出空间点源的速度场表达式

给出空间偶极的速度场表达式

5.3定常绕流与环量作用

5.4

库塔条件

库塔条件求升力

5.5

6

色散波

流体质点运动、压力分布

根据有限水深色散关系式，推导群速度的表达式

根据无限水深色散关系式，推导群速度的表达式

深水波的波能

写出流体力学N-S方程的无量纲形式

2024-11-13

四足

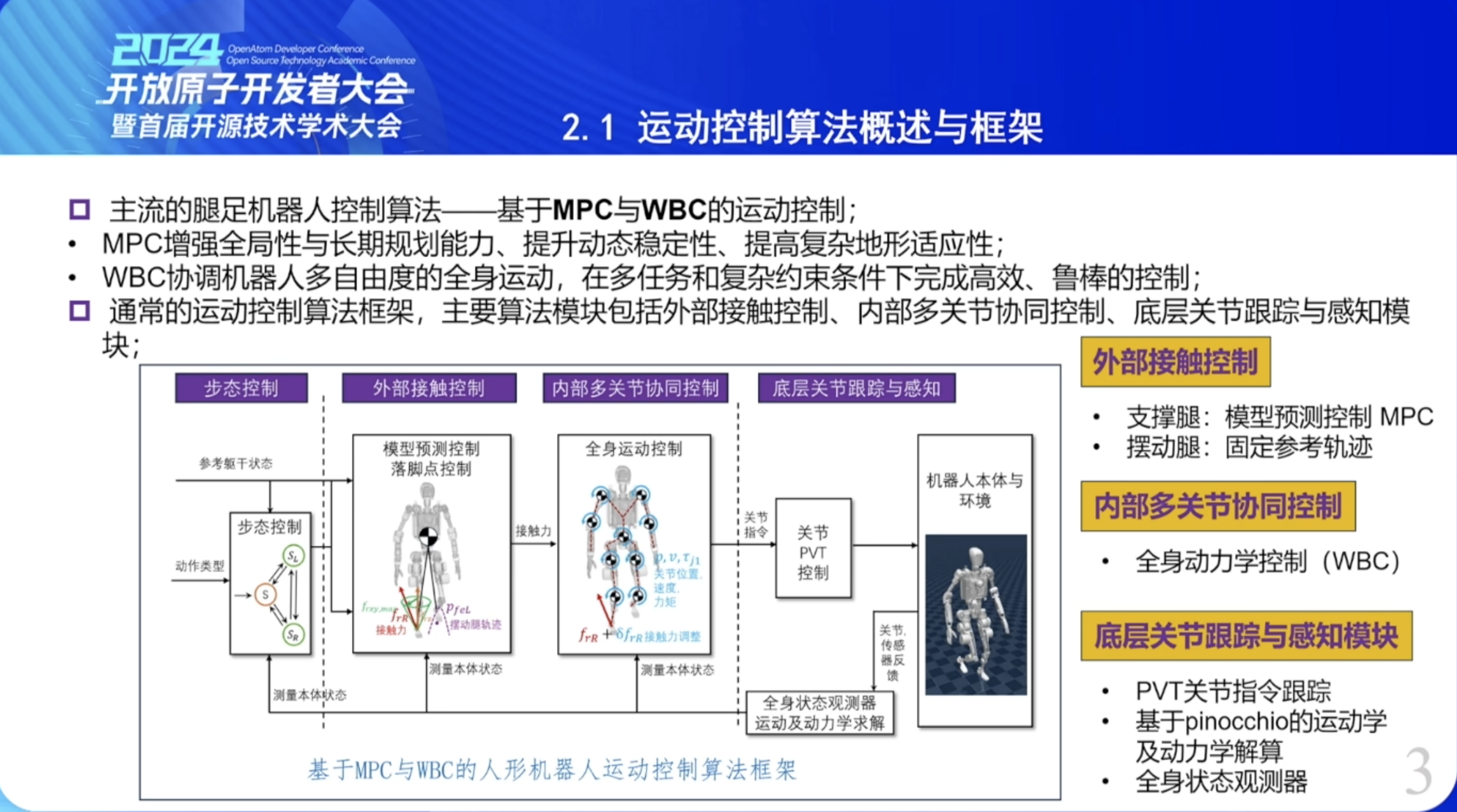
基于模型预测控制与全身控制的控制器

虚拟模型控制（VMC: Virtual Model Control）

通过模拟虚拟组件来产生所需的关节力矩,这些关节力矩产生的效果与虚拟组件产生的效果相同，因此实现了模拟组件与真实机器人连接的控制效果

全身控制（WBC）

为实现一组任务，所有驱动关节都能得到控制信号的控制系统都可以称作全身控制

WBC 使用了浮动基逆动力学

模型预测控制（MPC）试图在未来的一个滚动时域内，使用优化算法来跟踪给定的期望轨迹

设计一个基于模型预测控制与全身控制的控制器。在模型预测控制中，将整个机器人简化为一个单刚体模型并分析其动力学，建立状态方程、预测方程，将控制问题转化为一个优化问题，最终求出足底反力。在全身控制中，采用了多刚体动力学。四足机器人全身控制将整体的任务按照重要程度分为四个子任务，利用雅可比矩阵的零空间特性，保证低优先级的任务无法影响高优先级任务的控制。

legged_controller是入口

激光雷达

https://www.researching.cn/ArticlePdf/m00002/2022/59/18/1815006.pdf

武汉理工大学的初秀民、柳晨光等科研人员在《机械工程学报》2022年第4期发表了《无人水面艇三维激光雷达目标实时识别系统》

Virtual RobotX (VRX)

Virtual RobotX (VRX) 是一个开源的模拟环境，专门设计用于模拟无人水面车辆（USVs）在海洋环境中的操作

多功能 VRX 仿真环境作为一个可扩展的框架，致力于促进无人水面舰艇（USV）自主性的设计、开发和评估。VRX 仿真环境已被海事机器人研发社区所接受，不断发展以适应感知、学习和控制的进步，同时探索 USV 功能的新应用。

在这里插入图片描述

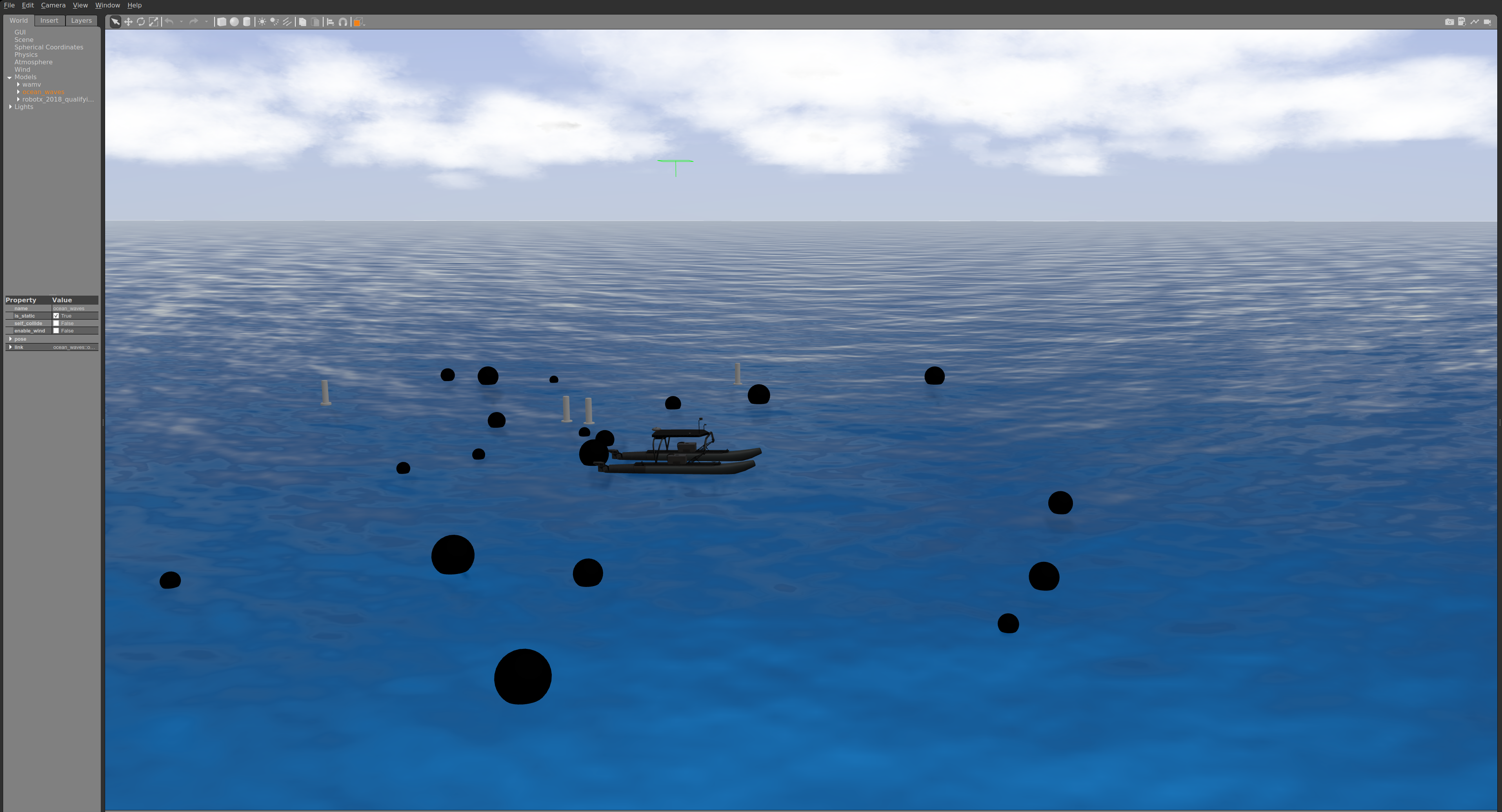
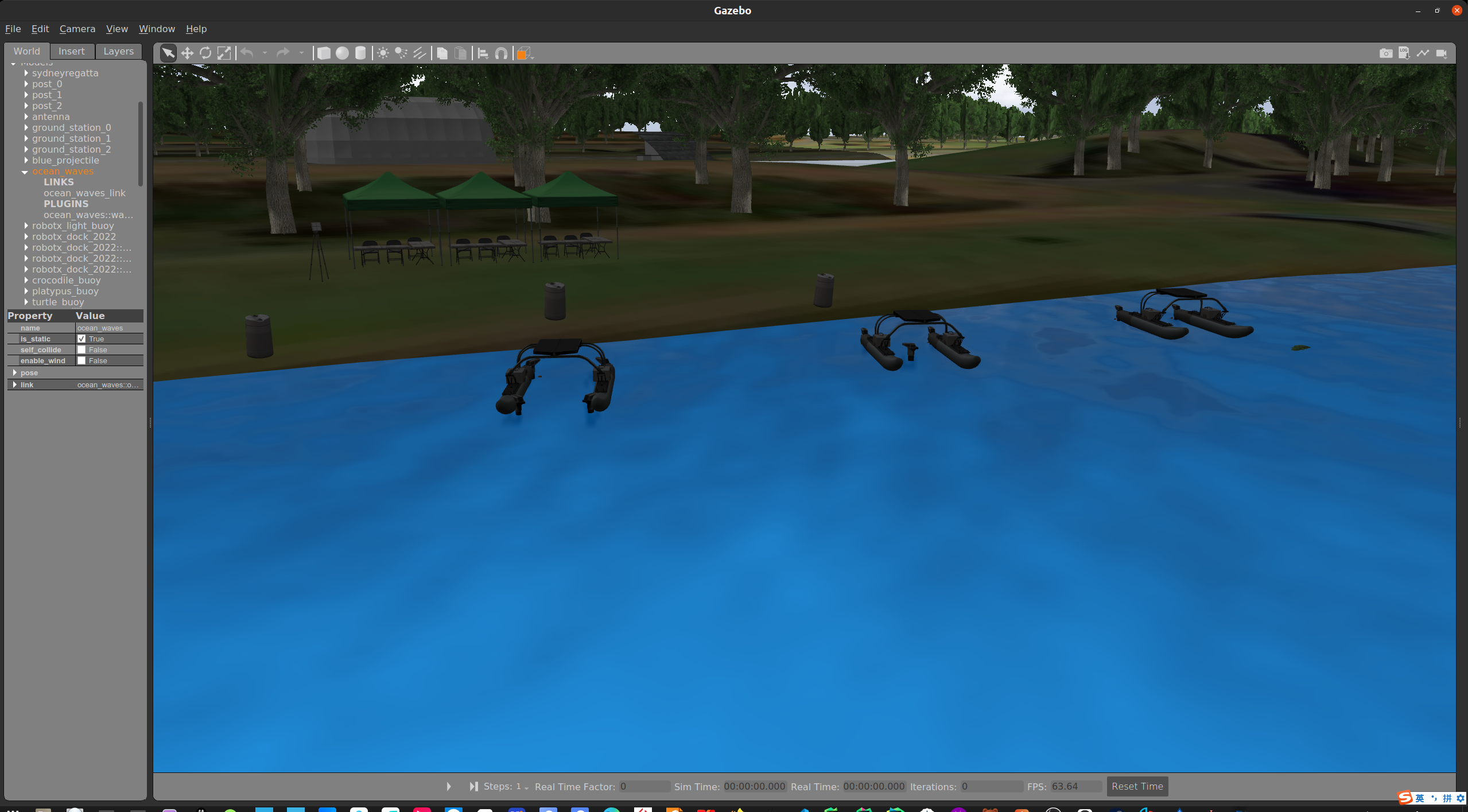
可以在世界中添加障碍等元素

可以创建自定义WAM-V推进器和传感器

不知道水下能不能仿真

Webots水下机器人仿真

uuv_simulator水下机器人仿真

https://github.com/uuvsimulator/uuv_simulator

矩阵就是坐标变换

矩阵的行列式就是是三维空间中立方体的体积的缩放比例

旋转矩阵式正交矩阵（三个列向量是一组标准正交基（单位向量+正交））

旋转矩阵的行列式恒为1（旋转矩阵不会缩放）

旋转矩阵逆等于转置

[旋转矩阵，欧拉角，四元数，旋转向量和齐次变换矩阵]

这几个名词都是用来描述一个物体的位置和姿态的

。旋转矩阵的初衷就是人们希望给定一个向量x，然后我对它旋转，能直接通过矩阵乘法的形式得到旋转后的向量坐标。也就是说y=Ax。这个方便计算机计算，因此旋转矩阵常用于编程。旋转矩阵是一个正交矩阵(AT=A−1AT=A−1)而且行列式是1。既然有了旋转矩阵那么为何还要欧拉角呢？这是因为我给你一个旋转矩阵，人看不懂它到底转了多少角度啊。计算机很容易算出来，但是对人来说非常困难。比如飞机驾驶员你让他以旋转矩阵的形式给飞机下指令，那人家不得疯了。而欧拉角那就非常直观，欧拉角就是我飞机头抬头多少(俯仰角pitch)，向左拐还是向右拐(偏航角yaw)，以及滚筒动作的角度(滚转角roll)。因此欧拉角一般是方便用户操作，或者程序员检查运算结果是否正确。然后有了欧拉角为何还要四元数呢？因为欧拉角有问题，即万向锁问题。欧拉角的意思是说旋转可以分解为绕机身，机翼，垂直机身三个轴旋转。注意了是依次旋转，每次旋转后的旋转轴姿态已经变化。看下图，比如你先绕机翼那个轴转90度，然后你会发现原先(第一幅图)的滚转角(即绕原先的机身转)与现在的偏航角(绕垂直机身的那个轴)重合了。也就是说滚转这个方向等与偏航了，两个自由度合并成一个了。这样一个麻烦就是如果一个给定旋转矩阵可能会计算出多个欧拉角。于是乎，数学家就用四元数来代替欧拉角。

旋转向量其实和欧拉角类似也会存在万向锁的，任何只用三个变量来描述姿态的方法都会产生万向锁。旋转向量就是方向与旋转轴相同，模为旋转角度的一个向量。之所以会用旋转向量是因为旋转矩阵用9个元素来描述三维的旋转，太浪费了。所以想用三个元素的向量来描述三维运动，这个向量就是旋转向量。齐次变换矩阵就是既包含旋转又包含平移的变换矩阵（它是4x4），旋转矩阵只包含旋转（它是3x3），齐次变换矩阵的左上角是旋转矩阵，右侧那列是平移量。

printf("%d\n",2.0);
输出：
2123684520

printf("%0.1f\n",2);
输出:
0.0

int n,m=0；
可以这样

不需要鼠标选取

直接光标所在行

Ctrl + / 　　　　　　　　　注释(取消注释)选择的行

Shift + Enter 　　　　　　开始新行

Ctrl + Y 　　　　　　　　删除当前插入符所在的行

Ctrl + D 　　　　　　　　复制当前行、或者选择的块

Ctrl + Delete 　　　　　　删除到字符结尾

Ctrl + Backspace 　　　　删除到字符的开始

Ctrl + Shift + NumPad+ 　　展开所有的代码块

Ctrl + Shift + NumPad- 　　收缩所有的代码块

ALT+ ←/→ 切换文件

SHIFT + ALT ←/→ 返回上次编辑的位置

CTRL+ALT+: emjo

/opt/glibc-2.34/lib/ld-linux-x86-64.so.2 --library-path /opt/glibc-2.34/lib:/lib/x86_64-linux-gnu ./yazi
q退出

char *rev
和
char review[]是一样的

char *rev[]
是数组里还是数组

    while (number > 0) {
        int digit = number % 10;  // 获取最低位
        printf("%d ", digit);      // 打印每一位
        number /= 10;              // 去掉最低位
    }

空格问题：scanf 使用 %s 读取字符串时，遇到空格、制表符或者换行符就会停止读取。因此，如果输入的字符串中有空格，scanf 只能获取到第一个单词。例如，输入 Hello World 时，scanf 只会读取 Hello，而 World 会被留在输入缓冲区。

int a = 10;
int &ref = a;  // 通过引用初始化 a

在编译时，编译器可能会将其转化为：

int a = 10;
int *ref = &a;  // ref 是指向 a 的指针，类似引用

&是赋值还是被赋值，等号左边还是右边

“~”符号的输出：Shift + Fn + Esc。 “`”符号的输出：Fn + Esc。

小脑（运动控制），以及大脑（具身智能）

Welcome to Rust!

This will download and install the official compiler for the Rust
programming language, and its package manager, Cargo.

Rustup metadata and toolchains will be installed into the Rustup
home directory, located at:

  /home/zgh/.rustup

This can be modified with the RUSTUP_HOME environment variable.

The Cargo home directory is located at:

  /home/zgh/.cargo

This can be modified with the CARGO_HOME environment variable.

The cargo, rustc, rustup and other commands will be added to
Cargo's bin directory, located at:

  /home/zgh/.cargo/bin

This path will then be added to your PATH environment variable by
modifying the profile files located at:

  /home/zgh/.profile
  /home/zgh/.bashrc

You can uninstall at any time with rustup self uninstall and
these changes will be reverted.

Current installation options:


   default host triple: x86_64-unknown-linux-gnu
     default toolchain: stable (default)
               profile: default
  modify PATH variable: yes

set(CMAKE_PREFIX_PATH "/opt/Qt/6.7.2/gcc_64")

`name="urdf_spawner"`

作用：指定该节点的名字。
意义：在 ROS 中，节点名称是全局唯一的标识，用于区分不同的节点。
例子

：
- urdf_spawner 是该节点的名字，表示它的功能是用来生成（spawn）一个 URDF 模型到 Gazebo 中。

`respawn="false"`

作用：指定节点是否在退出后自动重启。
选项

：
- false（默认值）：节点在退出后不会自动重启。
- true：如果节点因任何原因退出（例如崩溃），ROS 会自动尝试重新启动该节点。
意义

：
- 如果该节点负责关键功能（如控制器或监控器），可以设置为 true 确保系统稳定性。
- 在本例中，设置为 false，表明 urdf_spawner 节点在完成模型生成任务后不需要持续运行或重启。

`output="screen"`

作用：定义节点的日志输出方式。
选项

：
- screen：节点的日志输出会直接显示在终端中。
- log：节点的日志输出会写入 ROS 的日志文件（通常在 ~/.ros/log 文件夹中）。
意义

：
- 设置为 screen 有助于实时查看节点的运行信息（如错误信息或调试日志），适合在开发和调试阶段使用。
- 如果希望保存日志供后续分析，可以设置为 log。

controller_manager 是控制器的管理层：

负责加载和运行具体的控制器，包括 joint_state_controller。

joint_state_controller 是具体的状态发布控制器：

从硬件接口读取关节状态数据，并发布到 /joint_states 话题。

robot_state_publisher 是基于状态的姿态计算工具：

读取 /joint_states 中的关节数据，结合机器人模型生成 TF 坐标变换，用于可视化和坐标计算。

举例说明

假设我们有一个机械臂机器人，以下是如何使用这些组件：

控制器管理：
- 使用 controller_manager 动态加载和启动控制器，例如 joint_state_controller 和关节位置控制器。
状态发布：
- 启动 joint_state_controller，从硬件中获取关节状态并发布到 /joint_states。
姿态计算：
- 启动 robot_state_publisher，读取 /joint_states，根据 URDF 生成动态的 TF 坐标变换。
可视化：
- 在 RViz 中加载机器人模型，使用 TF 数据实时显示机器人在仿真或实际环境中的姿态变化。

2024-11-02

图形学

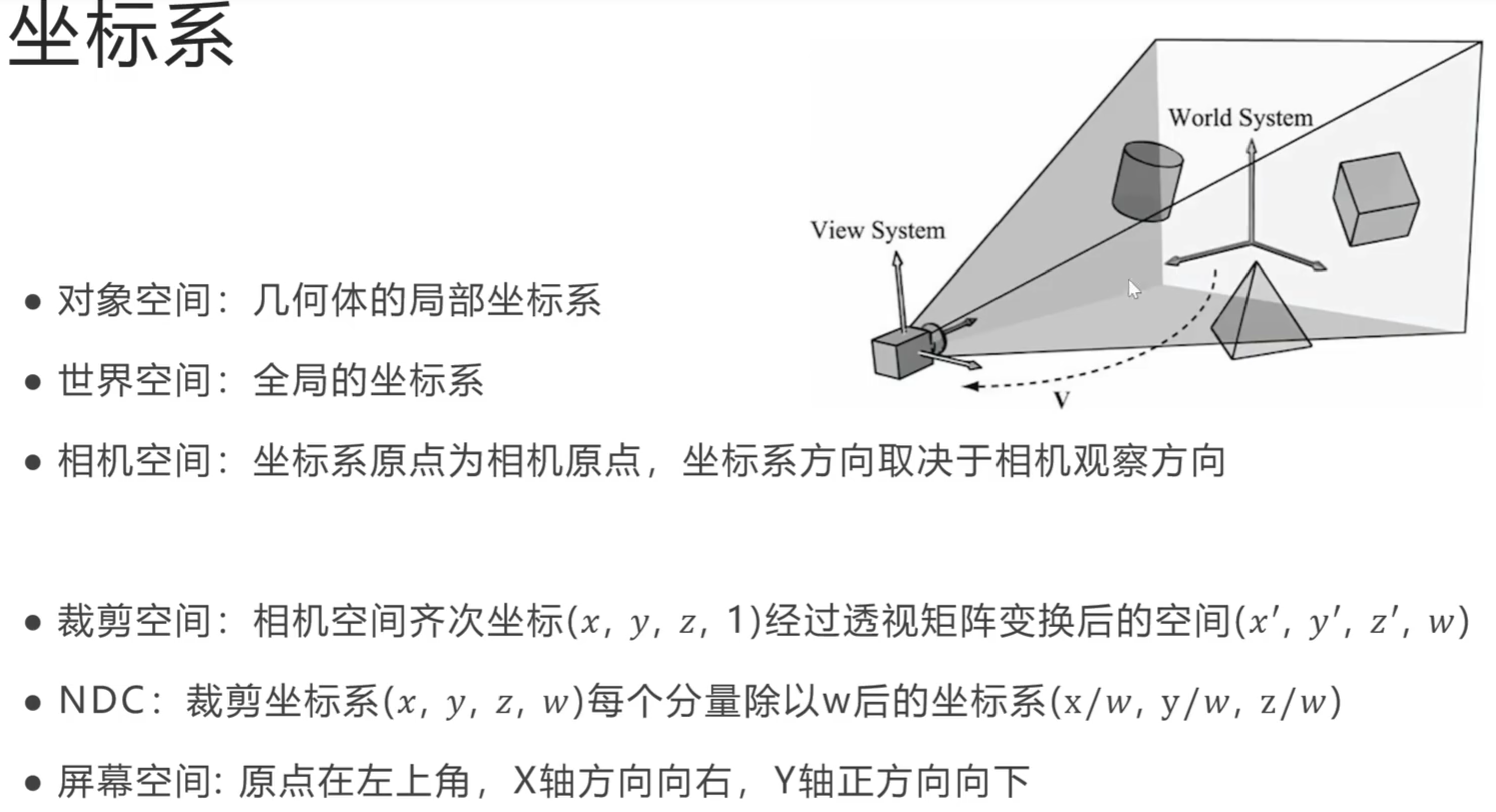
光线与球体的相交测试：

可以通过判断这个一元二次方程的delta判别式判断光线是否击中了球体

结构体：默认的成员访问权限是 public。

类：默认的成员访问权限是 private。

视口裁剪（Viewport Clipping）

视口裁剪是指在渲染过程中，图形系统根据当前的视口（viewport）大小和位置，裁剪出只在视口内的部分。这通常发生在将三维场景转换为二维图像时。

视口定义：视口是指在窗口或屏幕上的一个矩形区域，图形渲染的结果只显示在这个区域内。
用途：视口裁剪确保只绘制视口范围内的图形，避免无效的计算和渲染，提高效率。

透视裁剪（Perspective Clipping）

透视裁剪是指在透视投影过程中，决定哪些对象在视锥体内并且可见，从而只渲染可见部分。透视投影会产生一个视锥体，位于观察者与场景之间。

视锥体：在透视投影中，视锥体是一个从观察点（摄像机位置）向外扩展的锥形区域。只有位于这个区域内的对象才会被渲染。
裁剪：透视裁剪会去除视锥体外的对象，避免不必要的计算和渲染，并处理对象的深度关系。

总结

视口裁剪：关注的是最终图像在屏幕上的显示区域，只显示视口内的内容。
透视裁剪：关注的是三维场景中哪些对象在视锥体内，以决定哪些对象是可见的。

屏幕空间和 NDC（Normalized Device Coordinates）空间之间的关系:

坐标变换流程

在图形渲染过程中，顶点坐标经历多个变换，从世界空间到最终的屏幕空间，这个过程大致包括：

模型变换：将顶点从局部模型坐标转换到世界坐标。
视图变换：将世界坐标转换到相机坐标（视图空间）。
投影变换：将相机坐标转换到裁剪空间。
裁剪：将不在视野范围内的顶点剔除。
透视除法：将裁剪空间的坐标转换到 NDC 空间。这个步骤涉及将每个坐标的 x、y 和 z 分别除以 w（齐次坐标），使得坐标范围归一化到 [-1, 1]。

NDC 到屏幕空间的转换

一旦顶点处于 NDC 空间，它们需要被转换到屏幕空间：

视口变换：将 NDC 坐标映射到实际的屏幕像素坐标。视口变换使用屏幕的分辨率来进行坐标的线性变换。具体步骤是：
- 将 NDC 的 x 和 y 坐标从 [-1, 1] 范围映射到屏幕像素的范围。例如，对于一个宽度为 W，高度为 H 的屏幕：
  - screenX = (ndcX + 1) * 0.5 * (W - 1)
  - screenY = (1 - (ndcY + 1) * 0.5) * (H - 1)（Y 轴可能需要翻转，具体取决于坐标系统的定义）

NDC 空间 是一个归一化的坐标系统，主要用于在渲染管线中的处理，使得顶点坐标能够统一处理，不论目标显示设备的分辨率如何。
屏幕空间 是实际显示的坐标系统，与屏幕的物理尺寸和分辨率相关。
转换：通过视口变换，NDC 空间的坐标被转换为屏幕空间的像素坐标，从而最终呈现在用户的屏幕上。

NDC 空间可以看作是从三维世界到二维屏幕的中间步骤，而屏幕空间则是最终的输出结果。

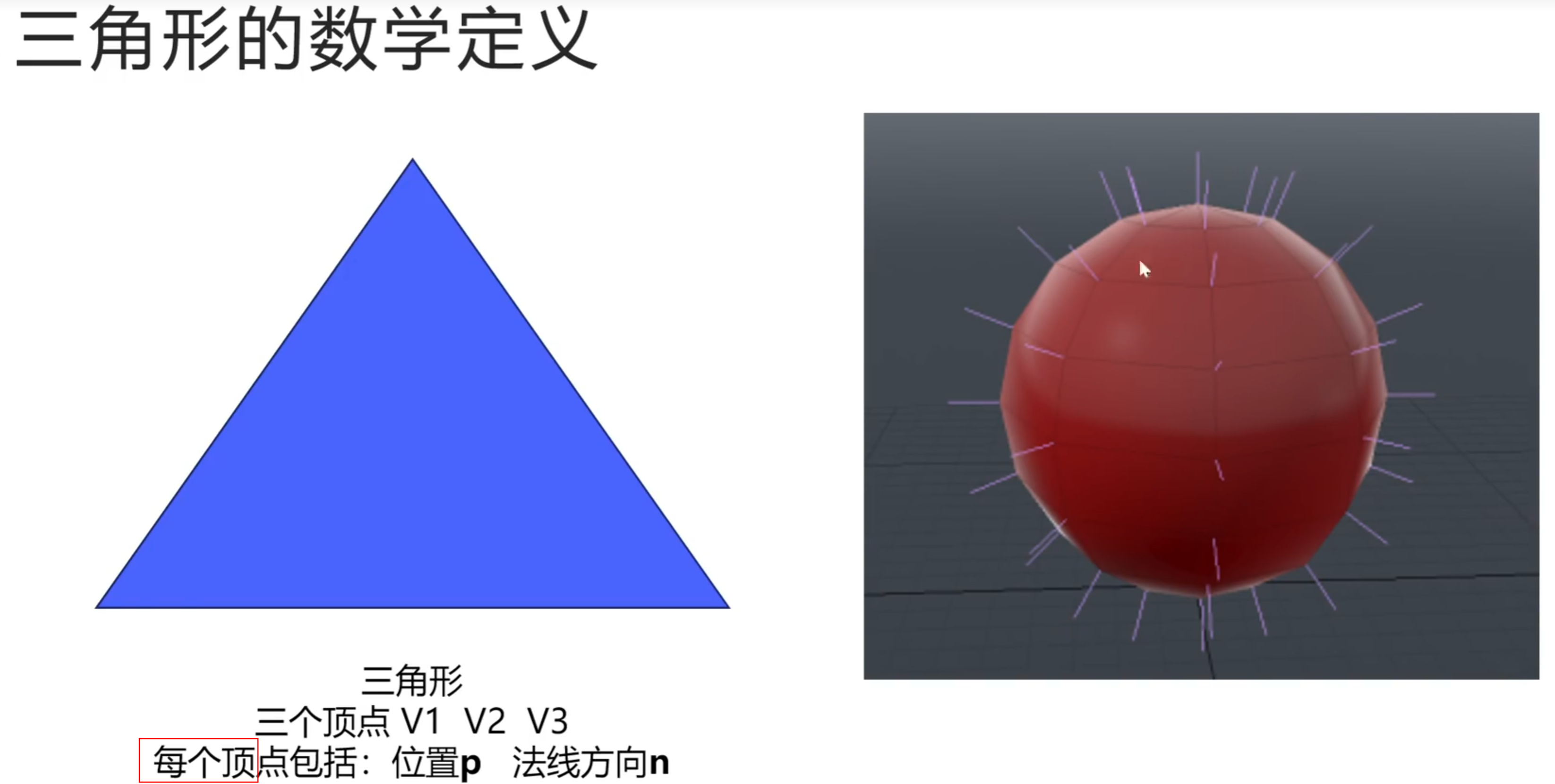
虚函数（Virtual Function）

定义：虚函数是在基类中声明为virtual的成员函数，可以在派生类中重写（override）。
实现：虚函数可以有具体的实现。基类中的虚函数可以提供默认的实现，派生类可以选择重写它。
对象创建：可以创建基类的对象，也可以创建派生类的对象。

纯虚函数（Pure Virtual Function）

定义：纯虚函数是在基类中声明为virtual并且等于0的函数。语法是virtual void functionName() = 0;。
实现：纯虚函数没有实现，基类通常不可以实例化。
对象创建：不能直接创建类的对象（即抽象类），只能创建派生类的对象。
用途：用于定义接口，强制派生类实现特定的函数

输入流操作符 (>>) 在处理流时，会自动跳过空格和其他空白字符（如换行符和制表符），直到遇到下一个有意义的值为止。因此，空格在这一过程中并不会被显式处理。

`line.compare(0, 2, "v ")` 的含义：

**0**：表示从 line 字符串的第一个字符开始进行比较。
**2**：表示比较的长度为 2，也就是说，只比较 line 字符串的前两个字符。
**"v "**：表示要将 line 字符串的前两个字符与字符串 "v " 进行比较。
如果 line 的前两个字符与 "v " 完全匹配，compare 方法返回 0。
如果不匹配，返回一个非 0 的值（具体的值取决于比较的结果：如果 line 字符串小于 "v "，返回一个负数；如果 line 字符串大于 "v "，返回一个正数）。

平面和场景

场景：管理世界空间下所有的形状（Shape）

平面的数学定义：

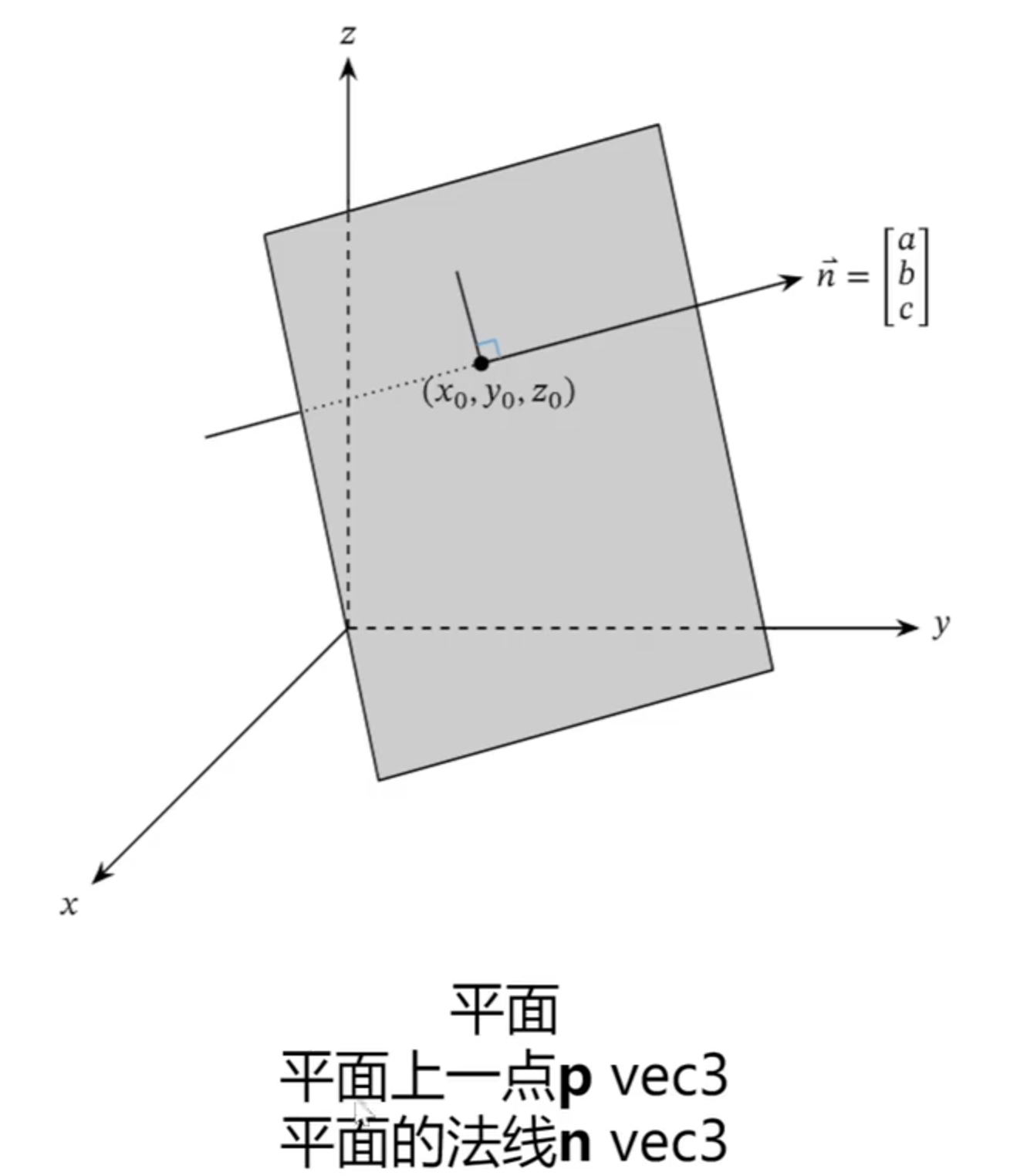
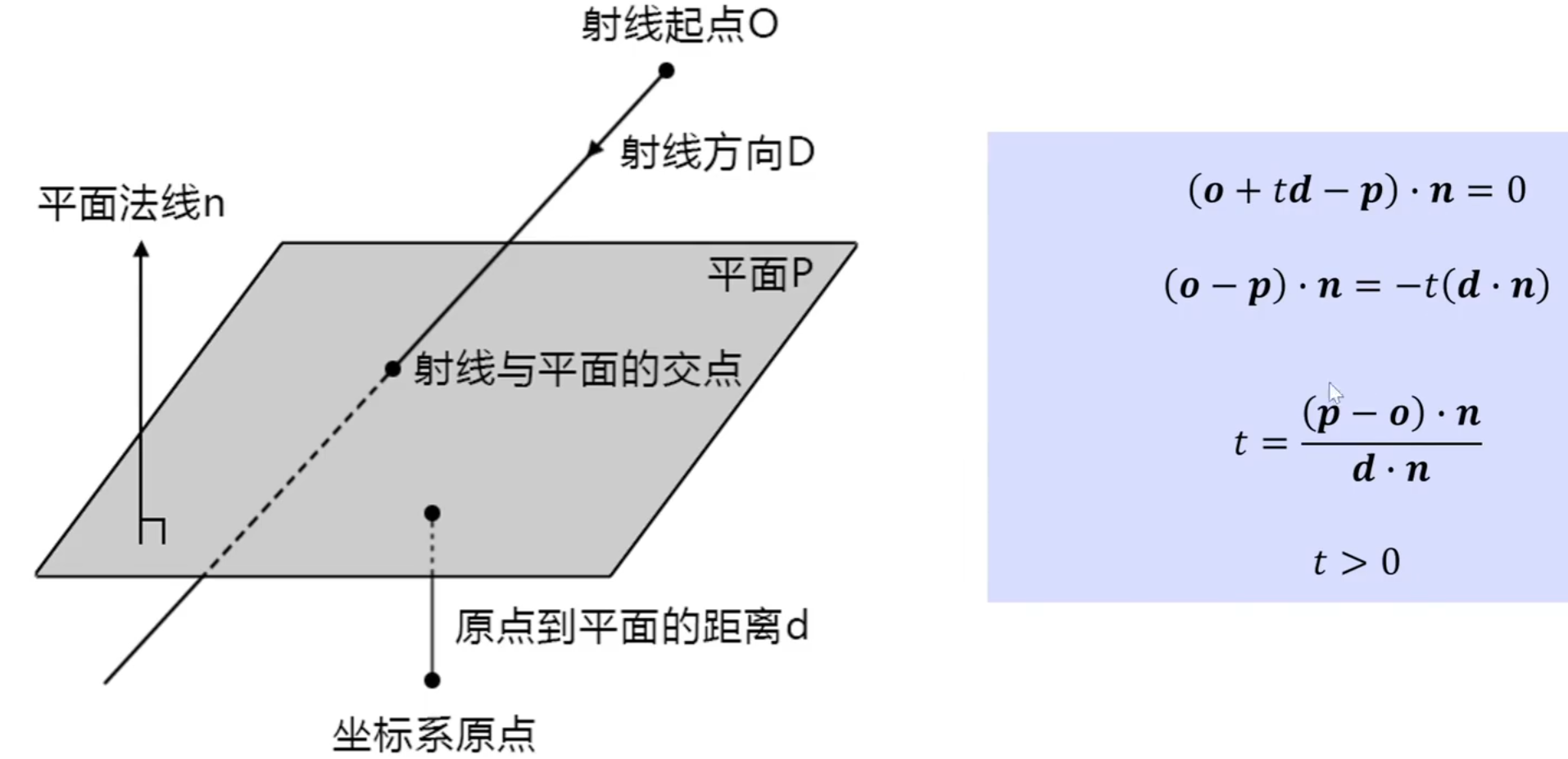
修改是为了改进多线程环境中的 线程安全性 和 竞态条件 的问题。我们来详细分析一下原始代码和修改后的代码之间的差异，以及为什么要这样修改。

原始代码：

count++; 
if (count % film.getWidth() == 0) {
    std::cout << static_cast<float>(count) / (film.getWidth() * film.getHeight()) << std::endl;
}

修改后的代码：

int n = ++count;
if (n % film.getWidth() == 0) {
    std::cout << static_cast<float>(n) / (film.getWidth() * film.getHeight()) << std::endl;
}

问题分析：

1. `count++` 是非原子操作

count++ 实际上是由 两个操作 组成的：读取 count 的值，然后 **增加 count**。在多线程环境中，如果多个线程同时执行 count++，就会发生 竞态条件（race condition），可能导致 count 的值增加不正确或者丢失。
例如，如果线程 A 和线程 B 同时读取到相同的 count 值，然后都加 1 写回，这样就会丢失一个递增的结果，导致 count 的值不准确。

2. `++count` 是原子操作

++count 是 自增并返回自增后的值，它在执行过程中是原子的，不会有并发冲突（前提是 count 本身是原子变量或操作）。这是因为它在自增的时候直接对 count 的值进行更新并返回，而不需要先读取再写入，避免了多个线程同时读取和写入的情况。

3. 存储递增结果到 `n`

修改后的代码 int n = ++count; 将自增后的结果保存在 n 中。这样做的好处是：
1. 保证了 count 更新后的值在后续代码中是确定的。如果我们直接在 if (count % film.getWidth() == 0) 中访问 count，其他线程可能会在我们检查 count 时修改它，导致判断条件不稳定。而 n 是在更新后的值保存时就固定了，因此后续的判断和输出使用 n 可以确保一致性。
2. 避免了 count 被其他线程修改时的影响。虽然 count 本身是全局共享的，但通过把递增结果保存在 n 中，我们保证了 n 的值不会在后续代码执行时被其他线程改动，确保了输出的正确性。

线程安全与性能考虑：

使用 int n = ++count; 的修改，确保了 每个线程对 count 的更新是安全的。同时，虽然 ++count 在某些情况下可能是原子操作，但若 count 是一个普通变量，并且没有显式的线程同步机制，那么可能仍然存在隐性的问题。将更新后的 count 值保存到 n 可以减少这种不确定性。
在多线程环境下，避免直接在条件判断中使用共享变量（如 count）是一个常见的做法，尤其是当这个变量在多个线程中共享且没有其他同步机制时。通过中间变量 n 来持有更新后的值，避免了在 count 被其他线程修改时产生的竞态条件。

        glm::translate(glm::mat4(1.f), pos) *
        glm::rotate(glm::mat4(1.f), glm::radians(rotate.z), { 0, 0, 1 }) *
        glm::rotate(glm::mat4(1.f), glm::radians(rotate.y), { 0, 1, 0 }) *
        glm::rotate(glm::mat4(1.f), glm::radians(rotate.x), { 1, 0, 0 }) *
        glm::scale(glm::mat4(1.f), scale)

glm::mat4(1.f)：创建一个单位矩阵，表示没有任何变换。
glm::translate(..., pos)：将矩阵平移到 pos 指定的位置，pos 是一个 glm::vec3 向量,表示物体在3D空间中的平移偏移量（x, y, z）。
glm::radians(rotate.z)：将角度 rotate.z 转换为弧度，因为GLM的 rotate 函数期望的旋转角度单位是弧度。
{ 0, 0, 1 }：指定旋转轴为Z轴。
glm::scale(glm::mat4(1.f), scale)：执行一个缩放变换，其中 scale 是一个 glm::vec3 向量，表示沿着X、Y和Z轴的缩放比例。例如，scale = { 2.f, 3.f, 1.f } 表示在X轴上放大2倍，在Y轴上放大3倍，而Z轴保持不变。

在GLM中，矩阵的乘法是从 右到左 进行的

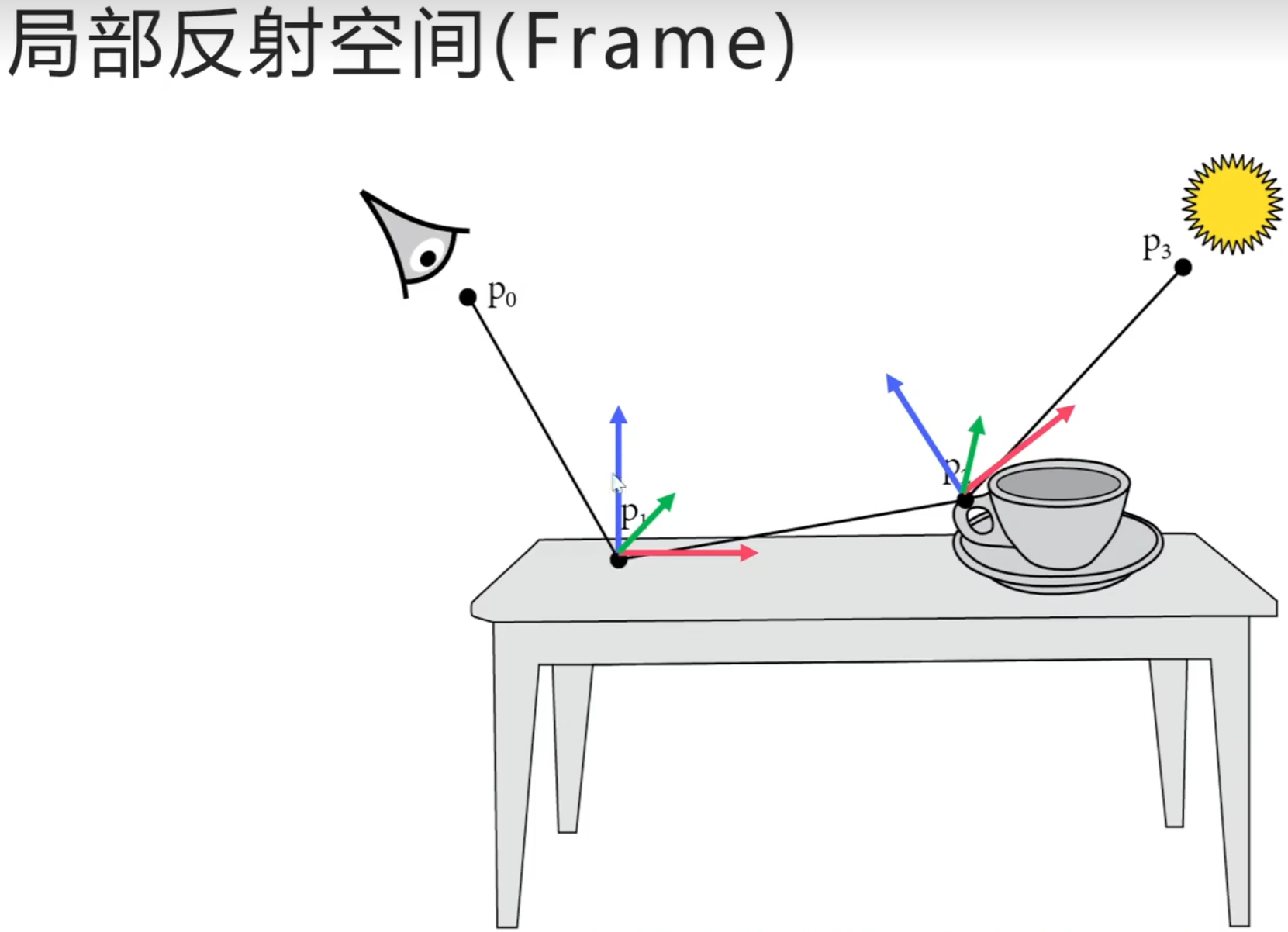
frame坐标系不用储存坐标系的原点，只用存储坐标轴的方向

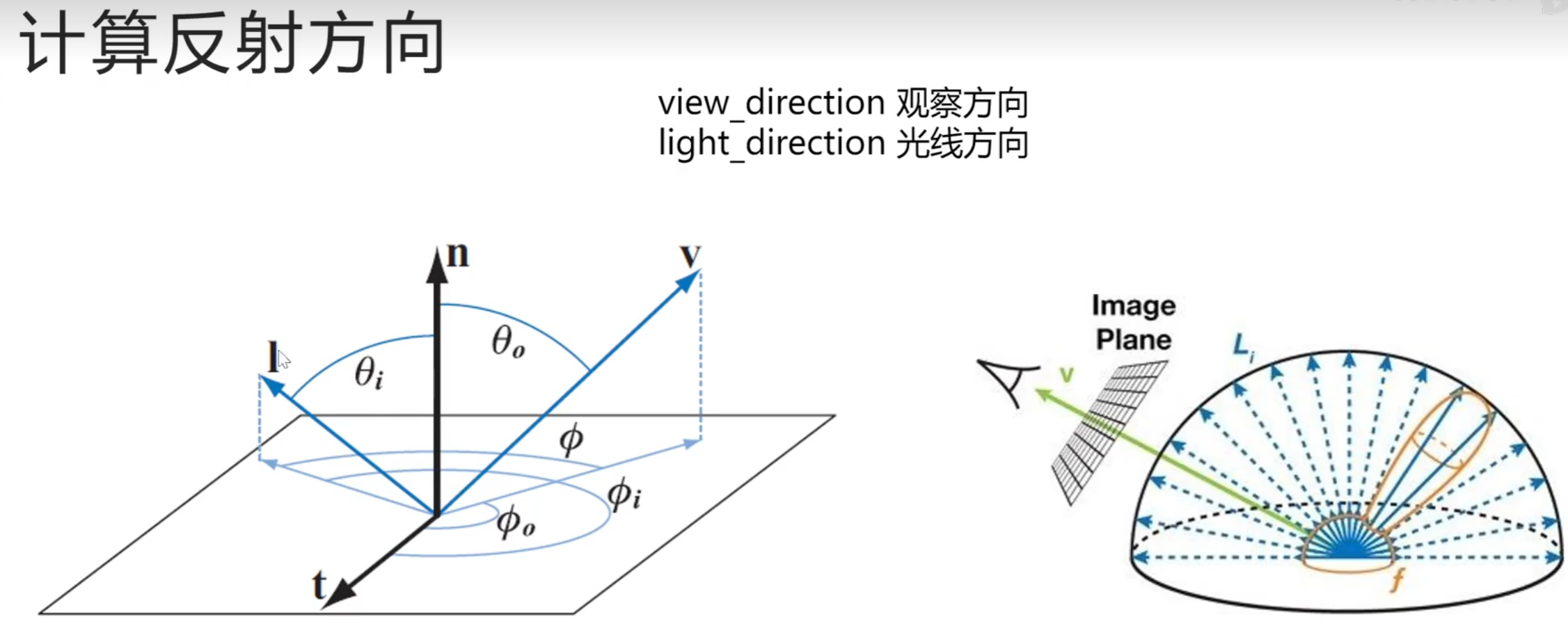
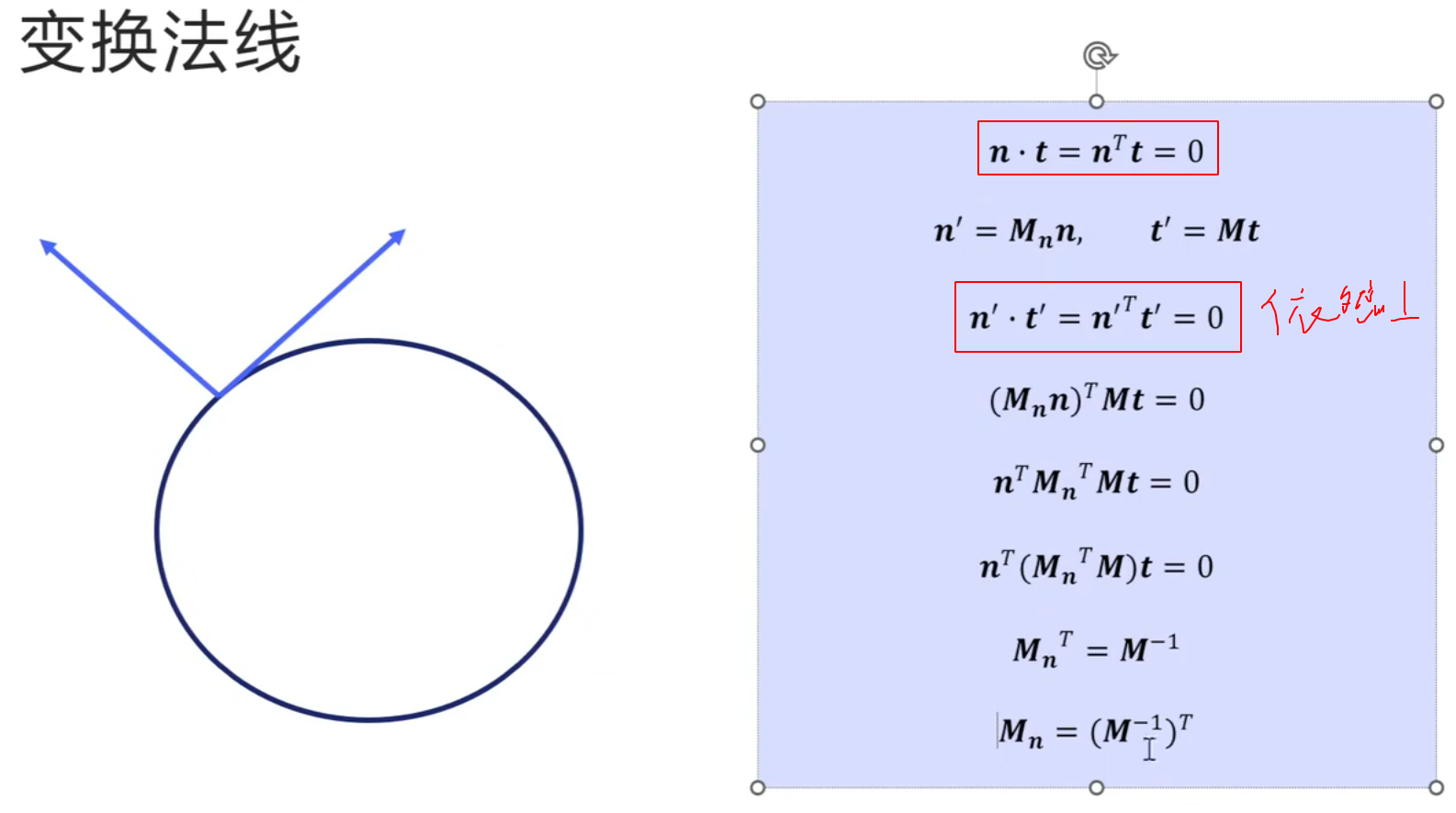
镜面反射：x,z取反

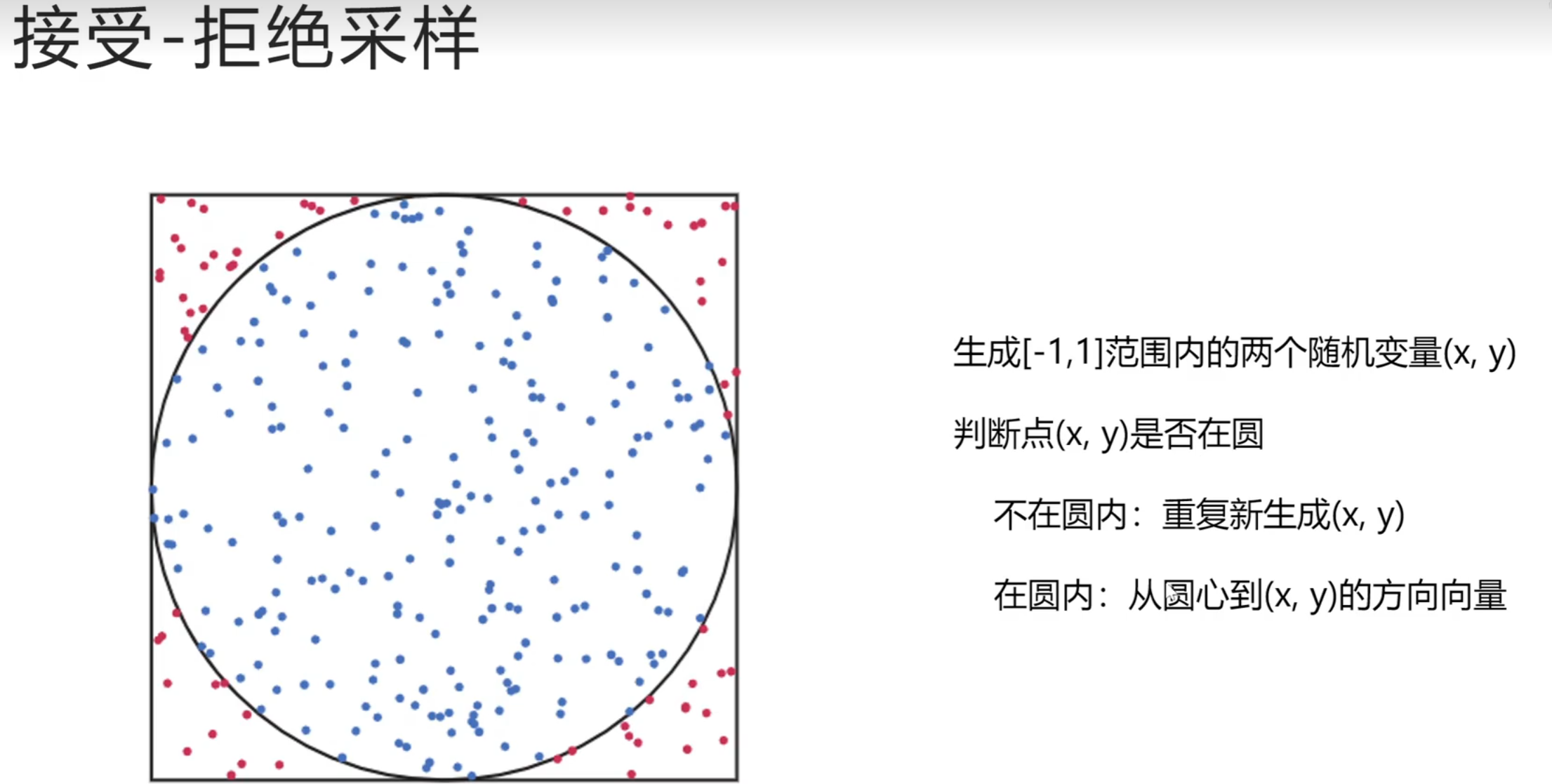
漫反射：采样

for (size_t i = 0; i < shapeInstances.size(); i++) {
    auto shapeInstance = shapeInstances[i];
    auto ray_object = ray.rayObjectFromWorld(shapeInstance.object_from_world);
    hitInfo = shapeInstance.shape.intersect(ray_object, t_min, t_max); // 需要把世界空间下的光线转换成对象空间里相交测试
    if (hitInfo.has_value()) {
        t_max = hitInfo->distance;
        closest_hitInfo = hitInfo;
        closest_instance = &shapeInstance;
    }
}

与：

    for (size_t i = 0; i < shapeInstances.size(); i++) {
        auto ray_object = ray.rayObjectFromWorld(shapeInstances[i].object_from_world);
        hitInfo = shapeInstances[i].shape.intersect(ray_object, t_min, t_max); //需要把世界空间下的光线转换成对象空间里相交测试
        if (hitInfo.has_value()) {
            t_max = hitInfo->distance;
            closest_hitInfo = hitInfo;
            closest_instance = &shapeInstances[i];
        }
    }

看似一样，实则不一样

第一个是拷贝，

shapeInstance 就是一个独立的对象，它与原始 shapeInstances[i] 没有直接关系

减小光追的噪点：

2024-10-27

motion_planning

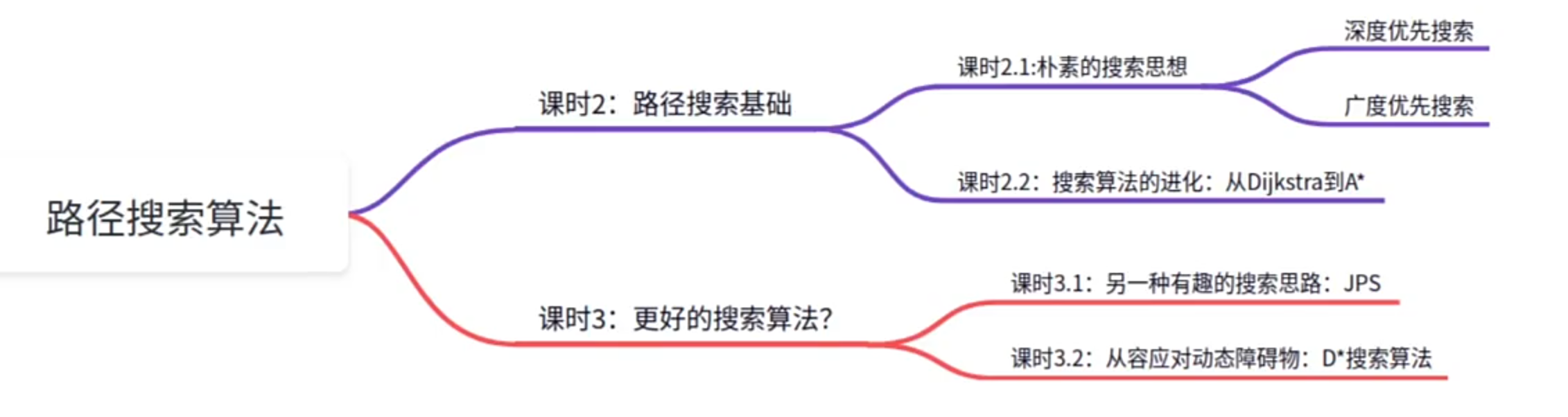
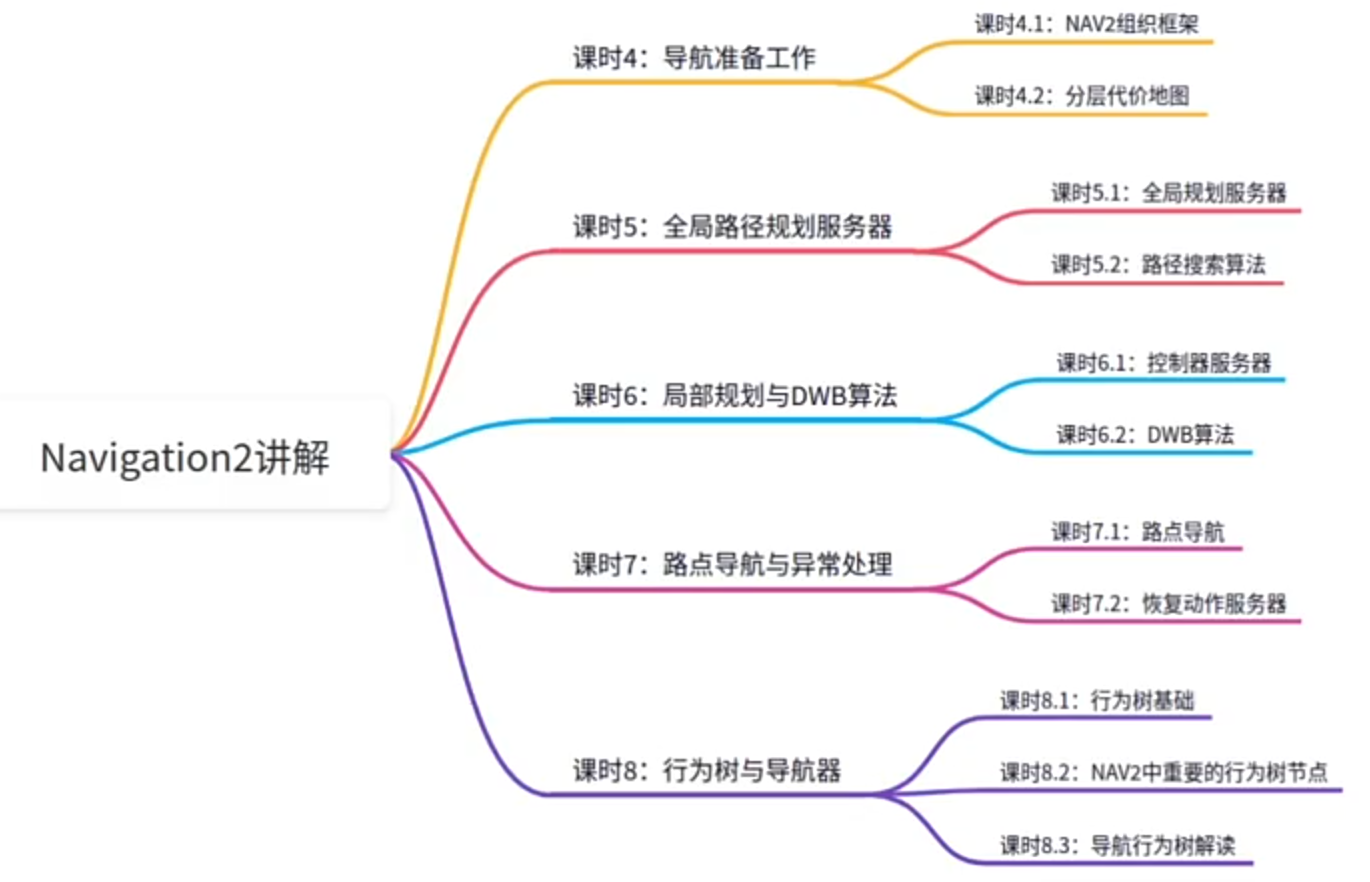
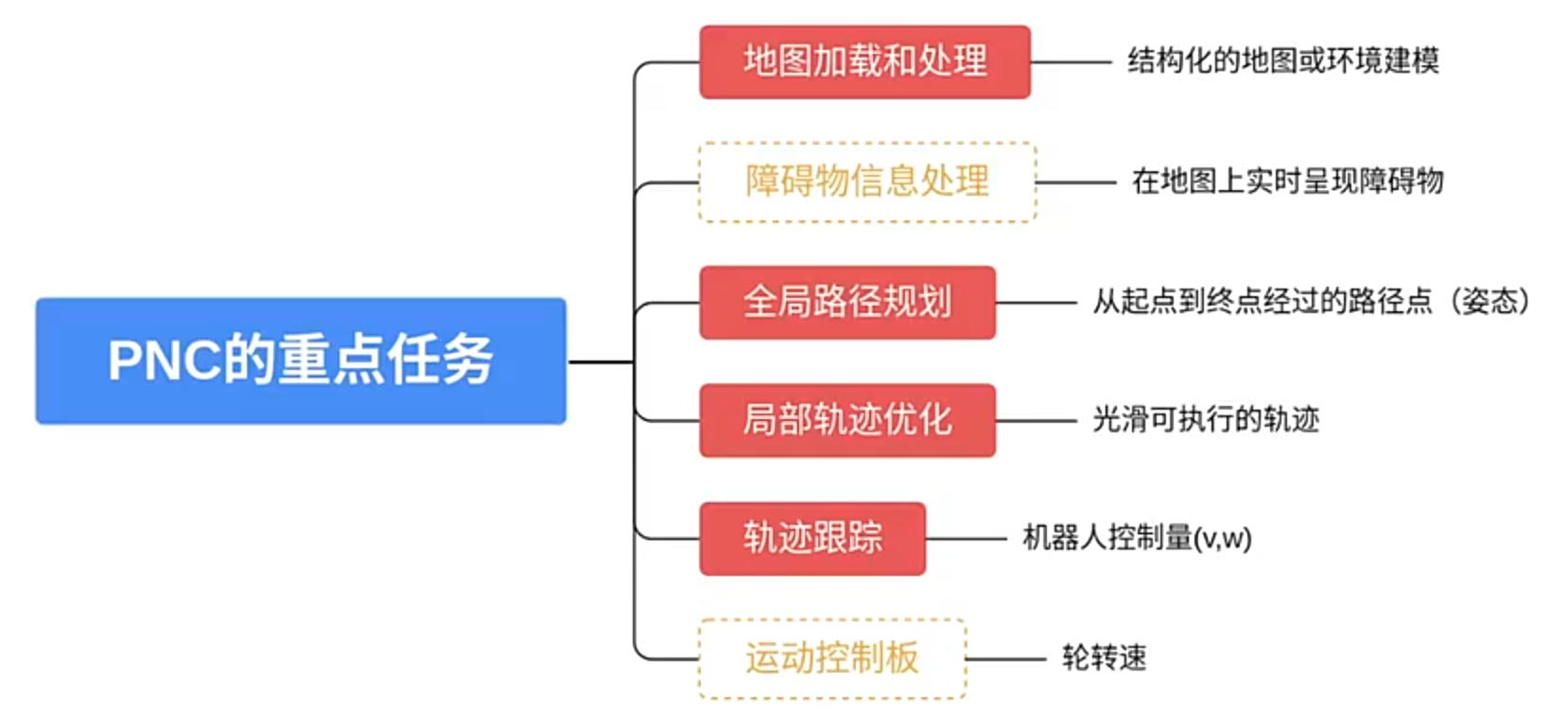
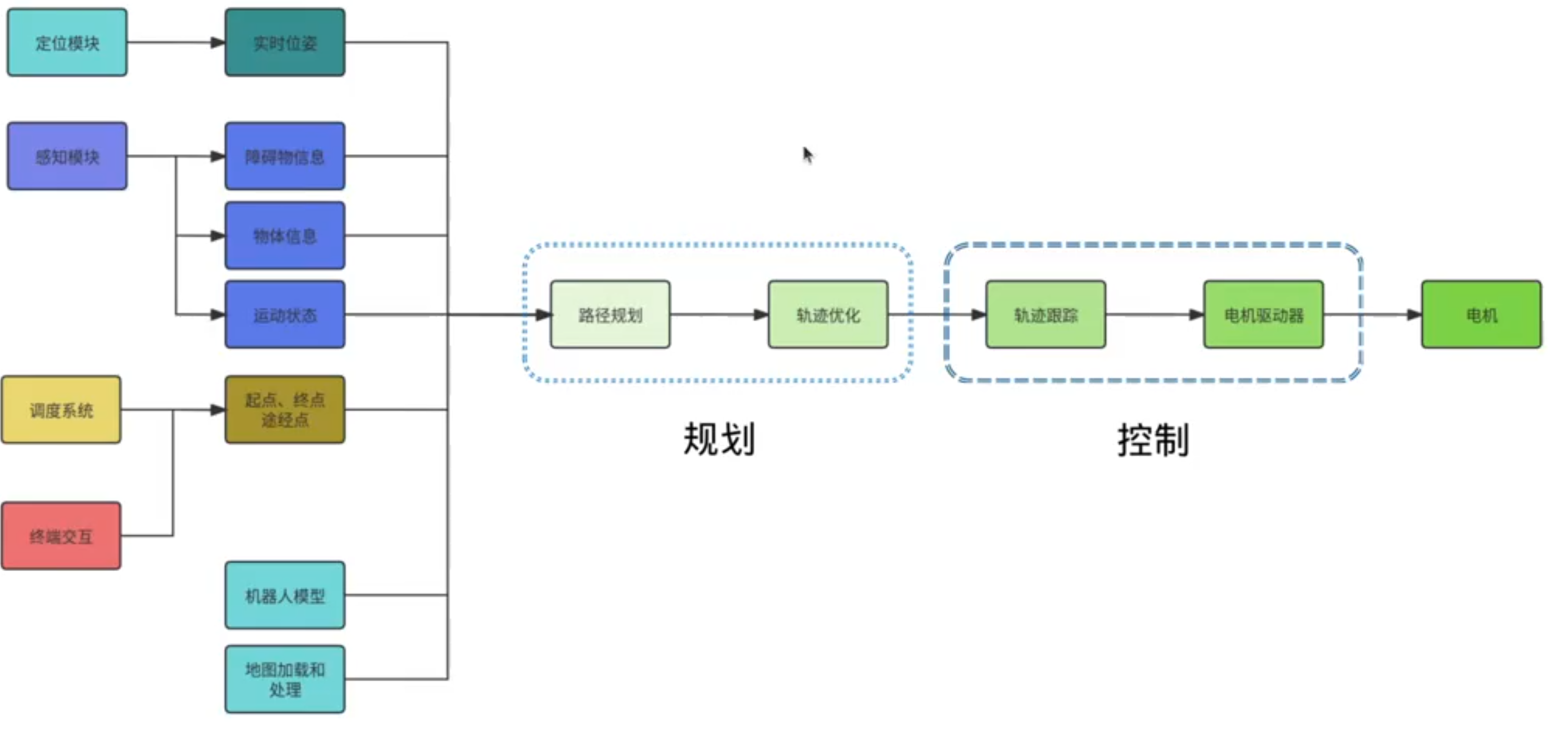
地图处理：

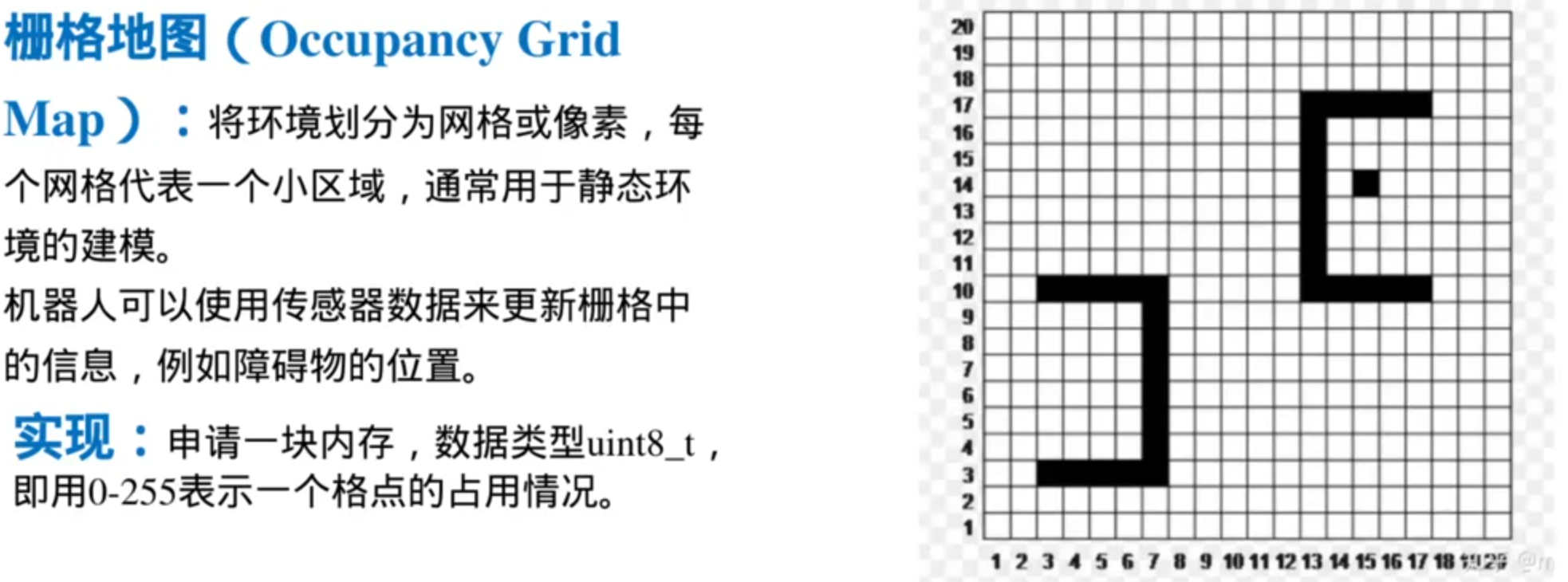
Octree Map存储效率高，占用内存小，适合三维空间

缺点：构建和查询比较复杂，需要递归操作

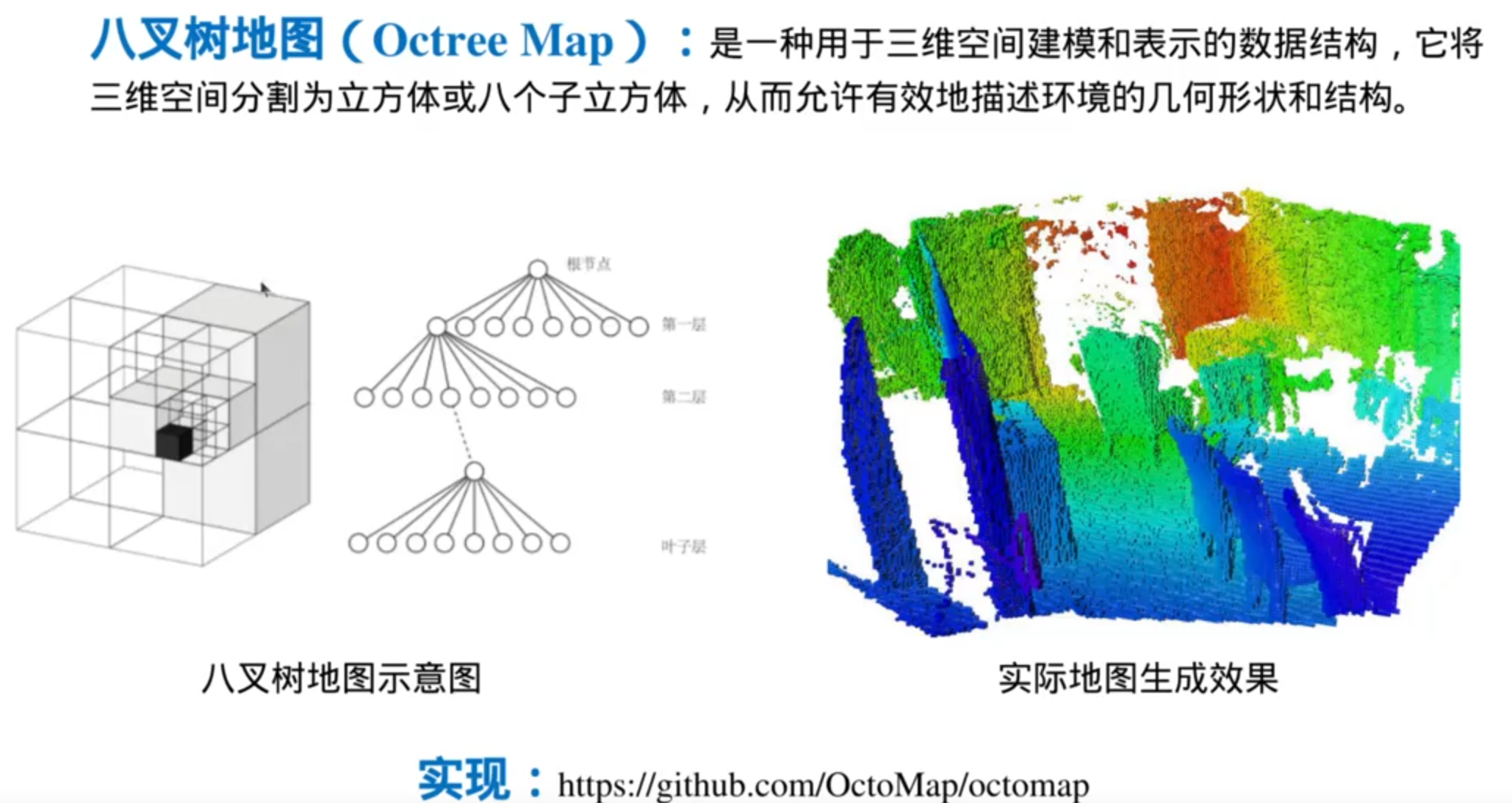
对于平面，可以使用四叉树地图

拓扑地图

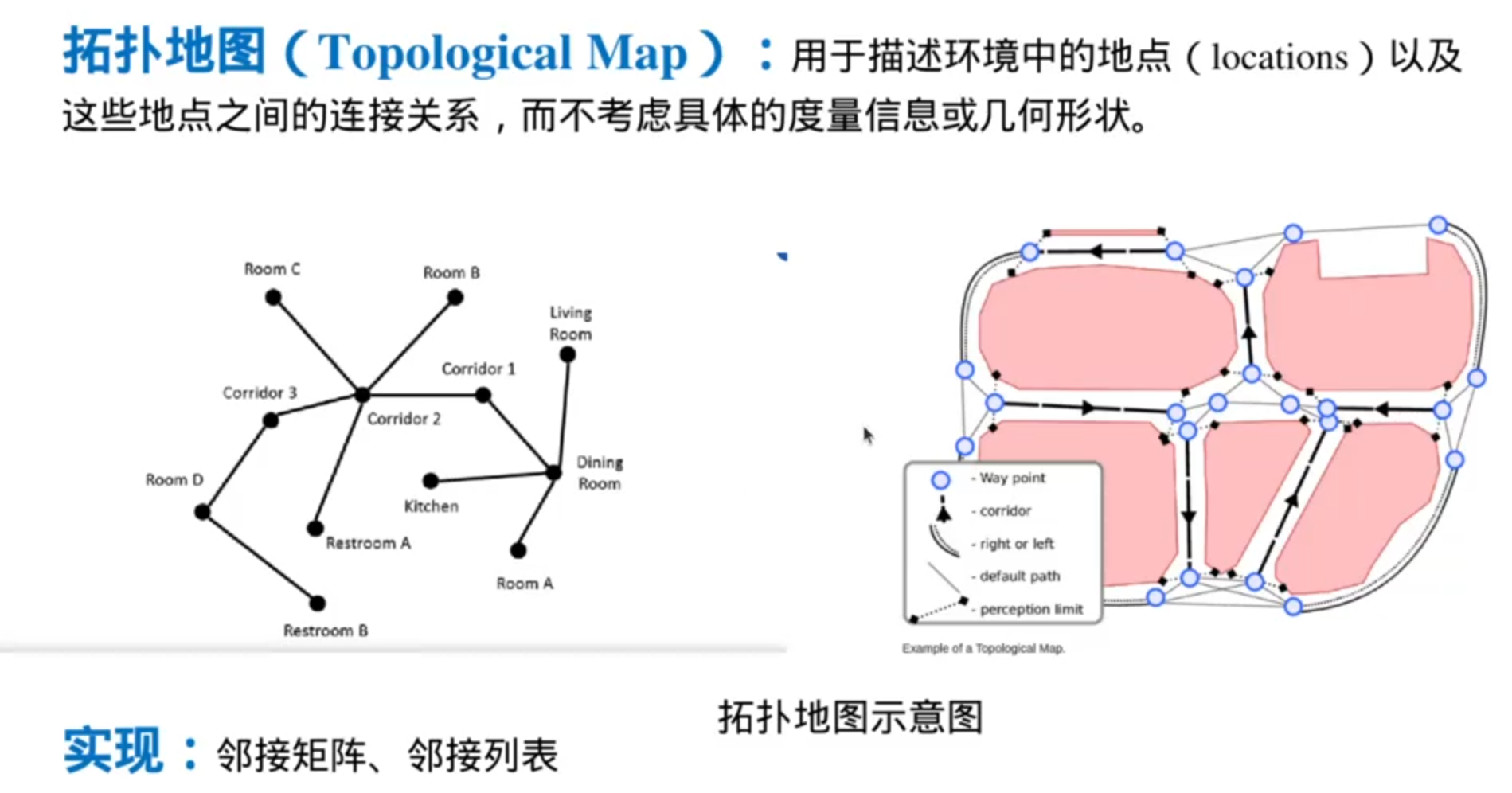
不能生成具体的路径

欧式距离场地图

每一个像素点的值是到目标点的距离

高精地图+激光雷达：

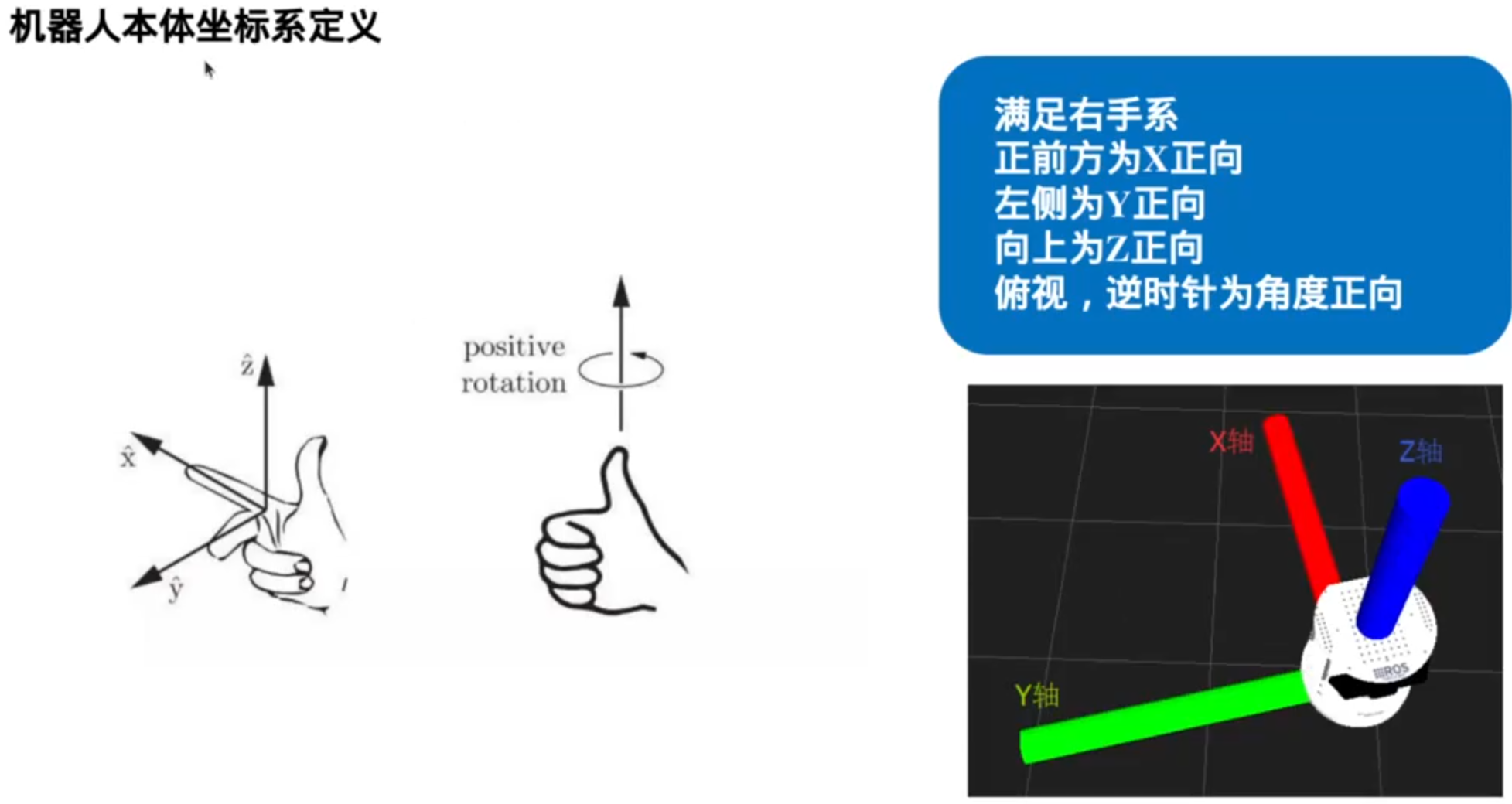
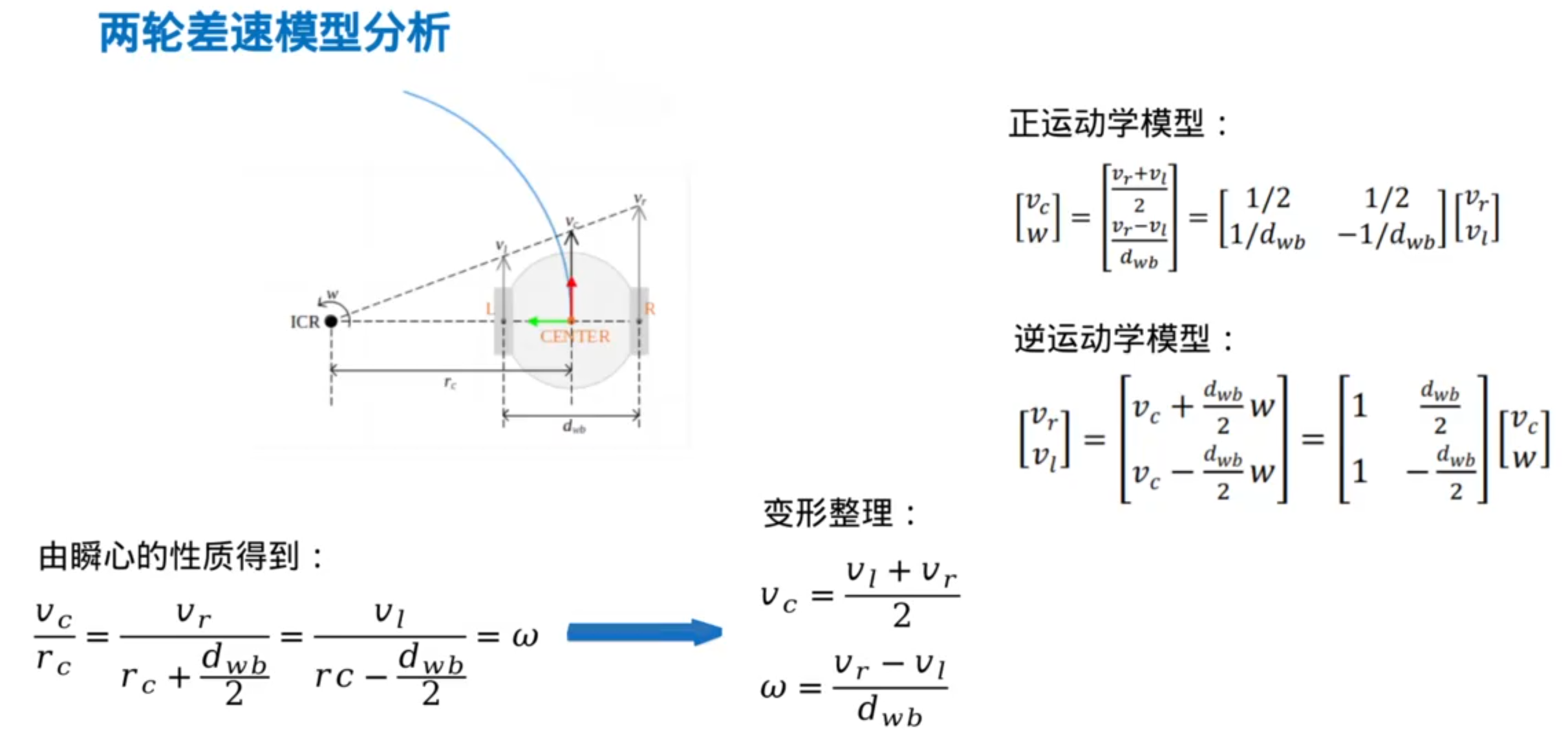
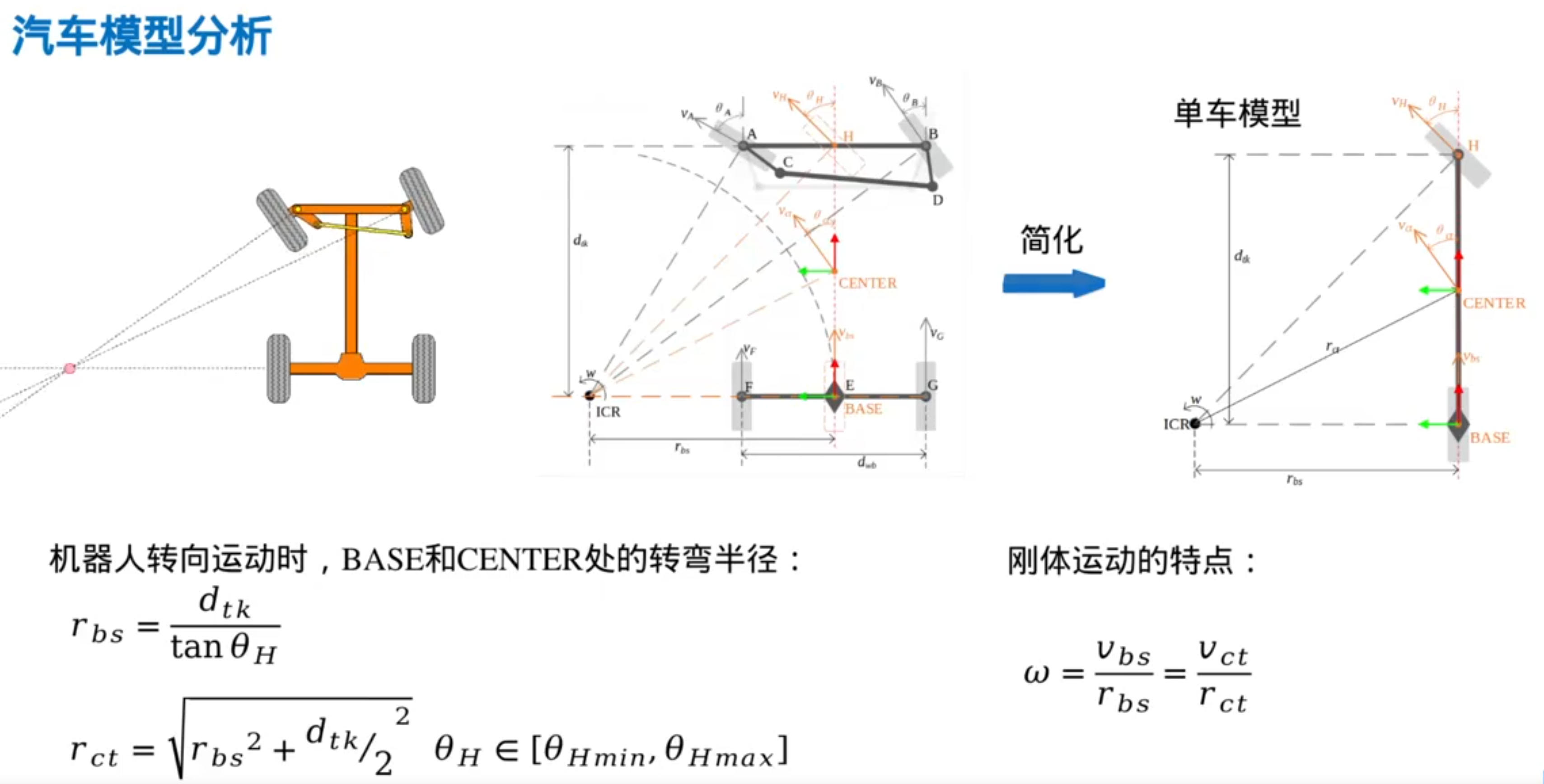
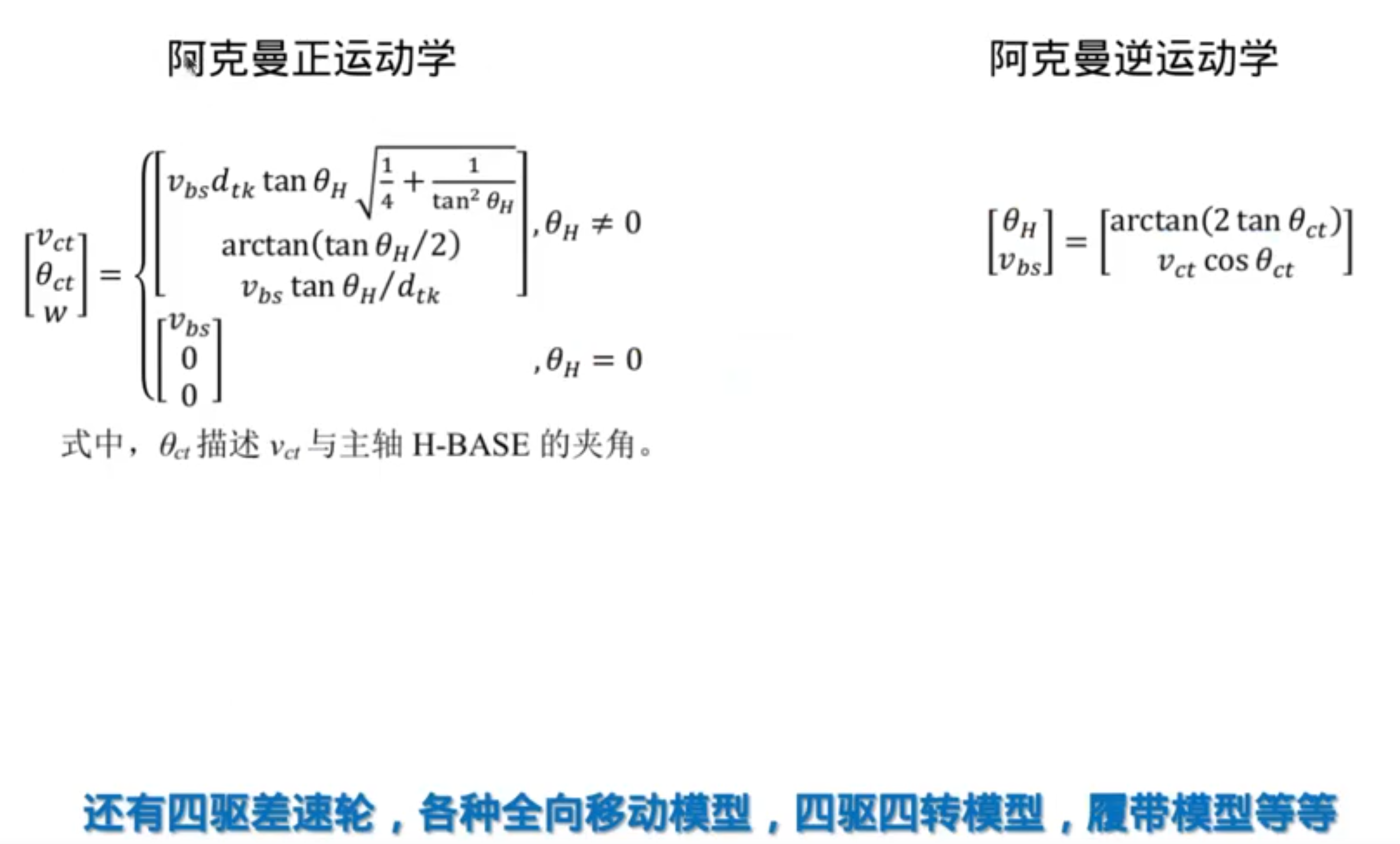
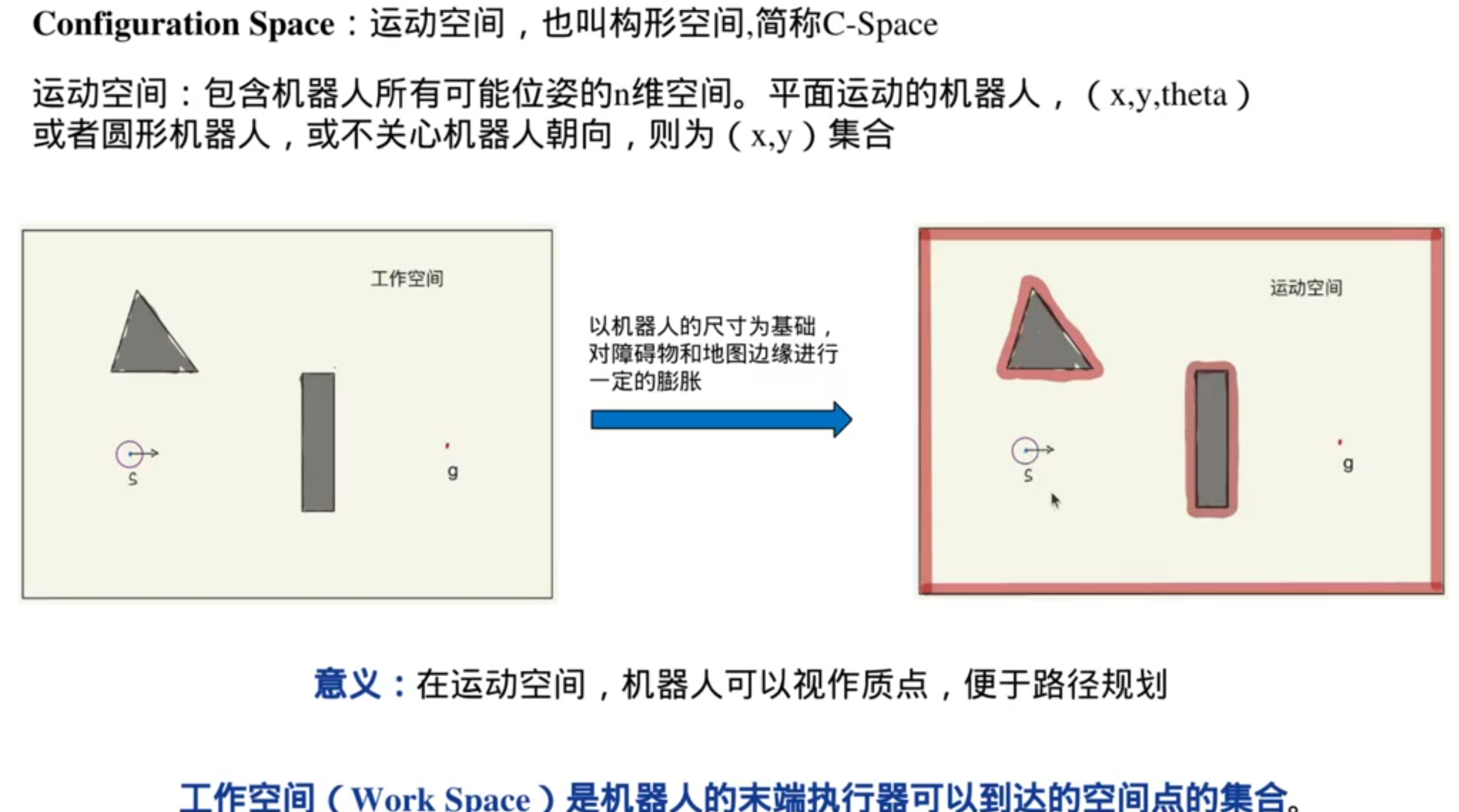
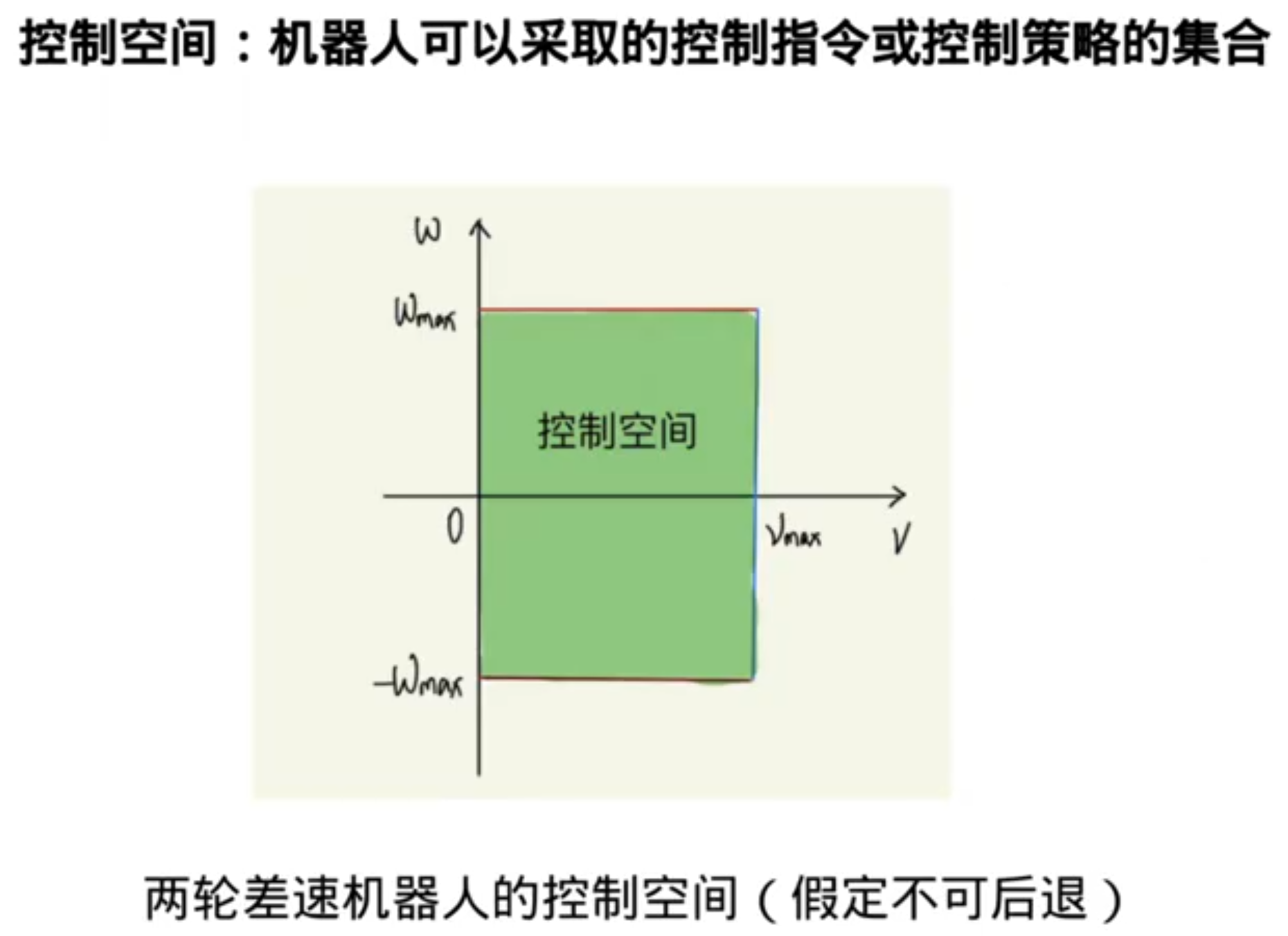
基于结构化地图（已经使用数据结构/储存方式存储好了环境信息）的搜索：

基于采样的路径搜索算法（不太适用于移动机器人）

没有地图的算法：概率路图

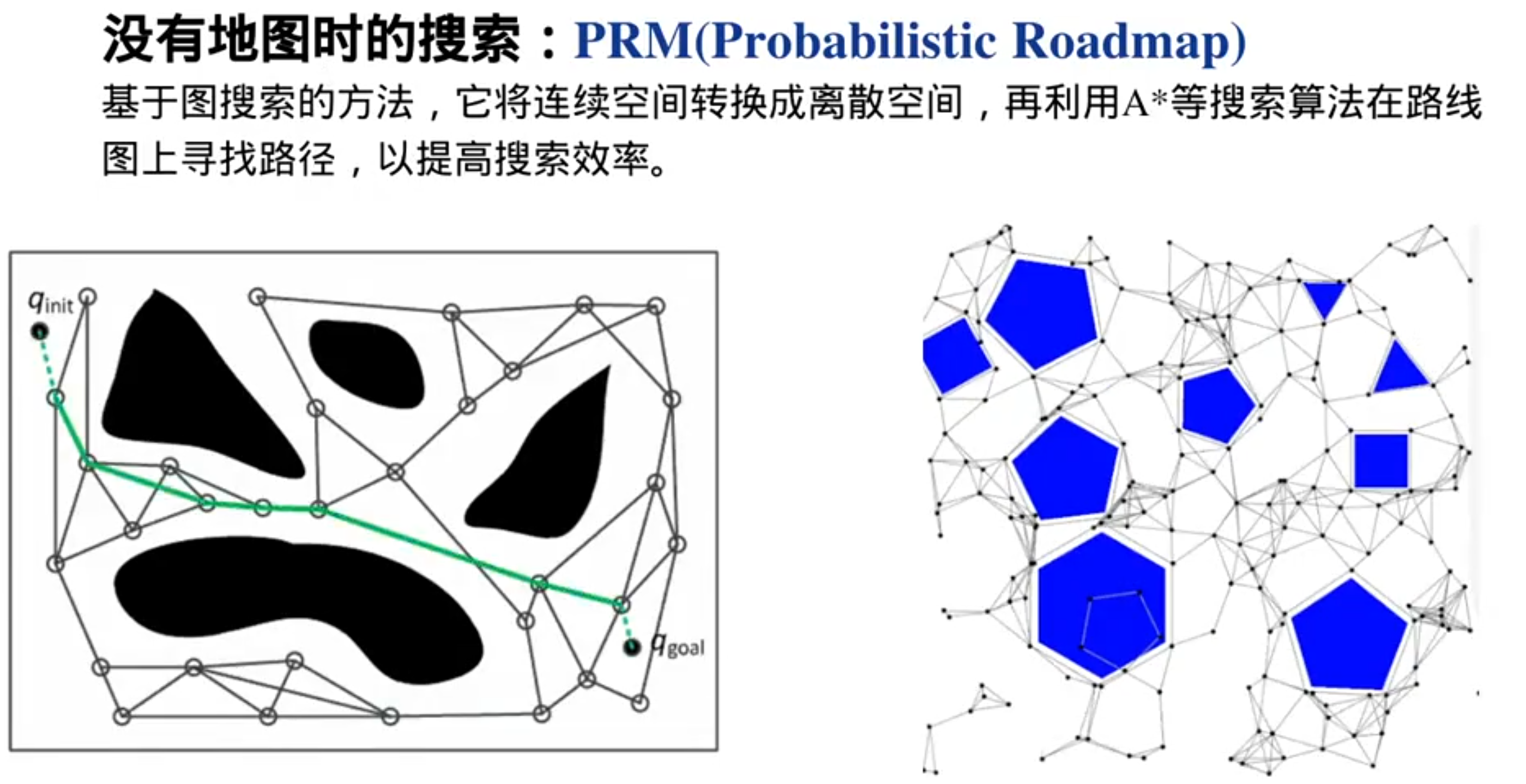
没有地图，先构造地图：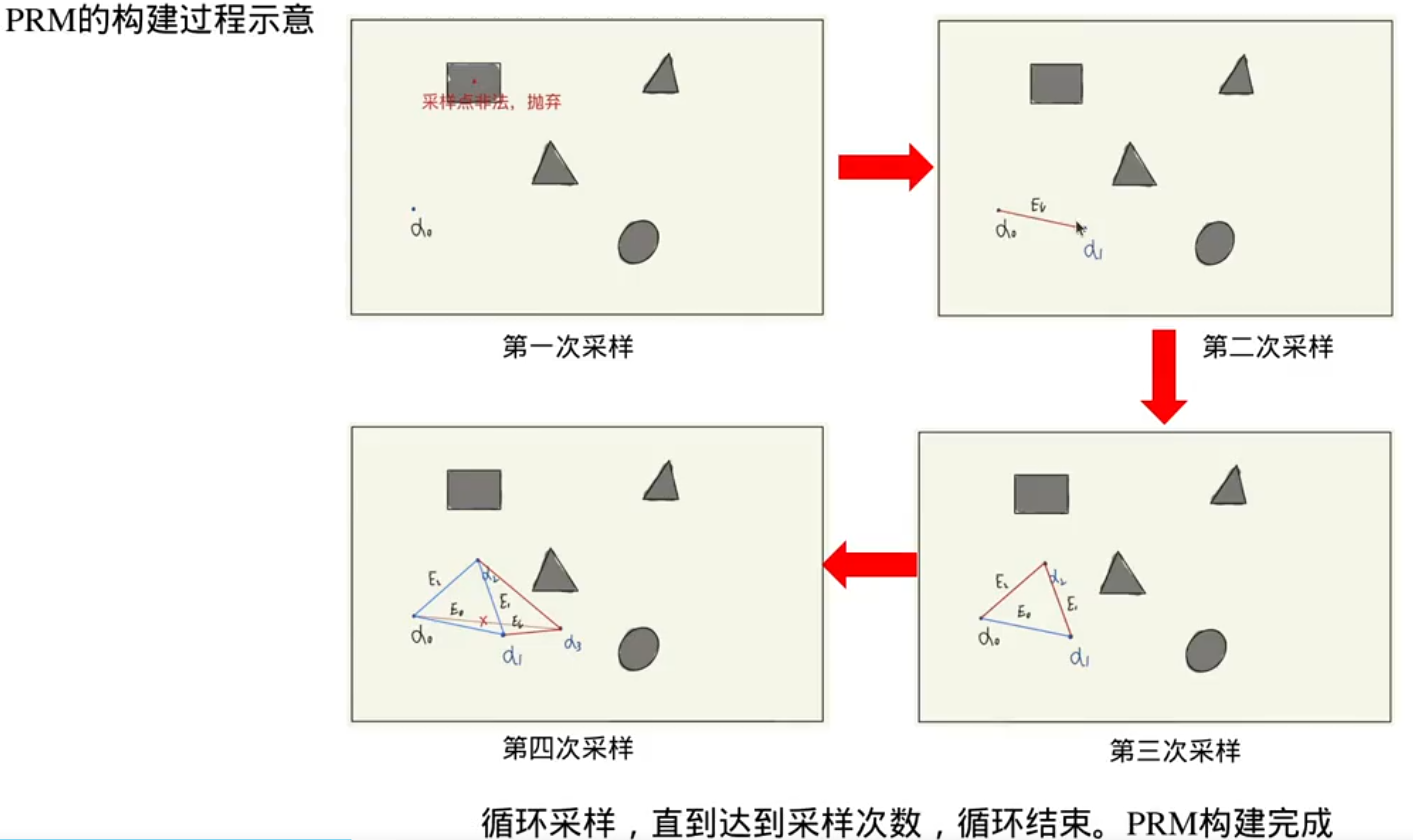

建完图后路径规划：

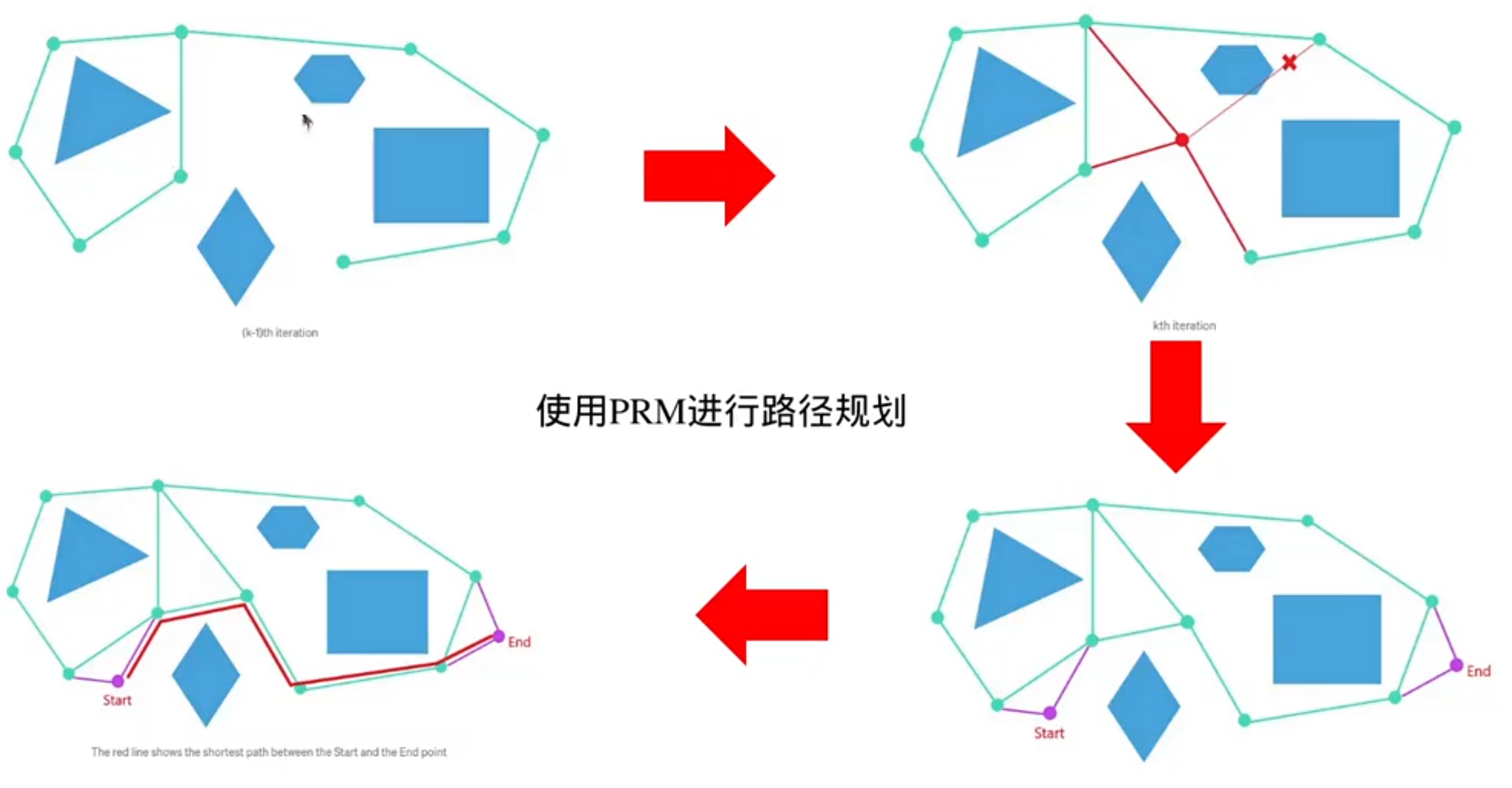
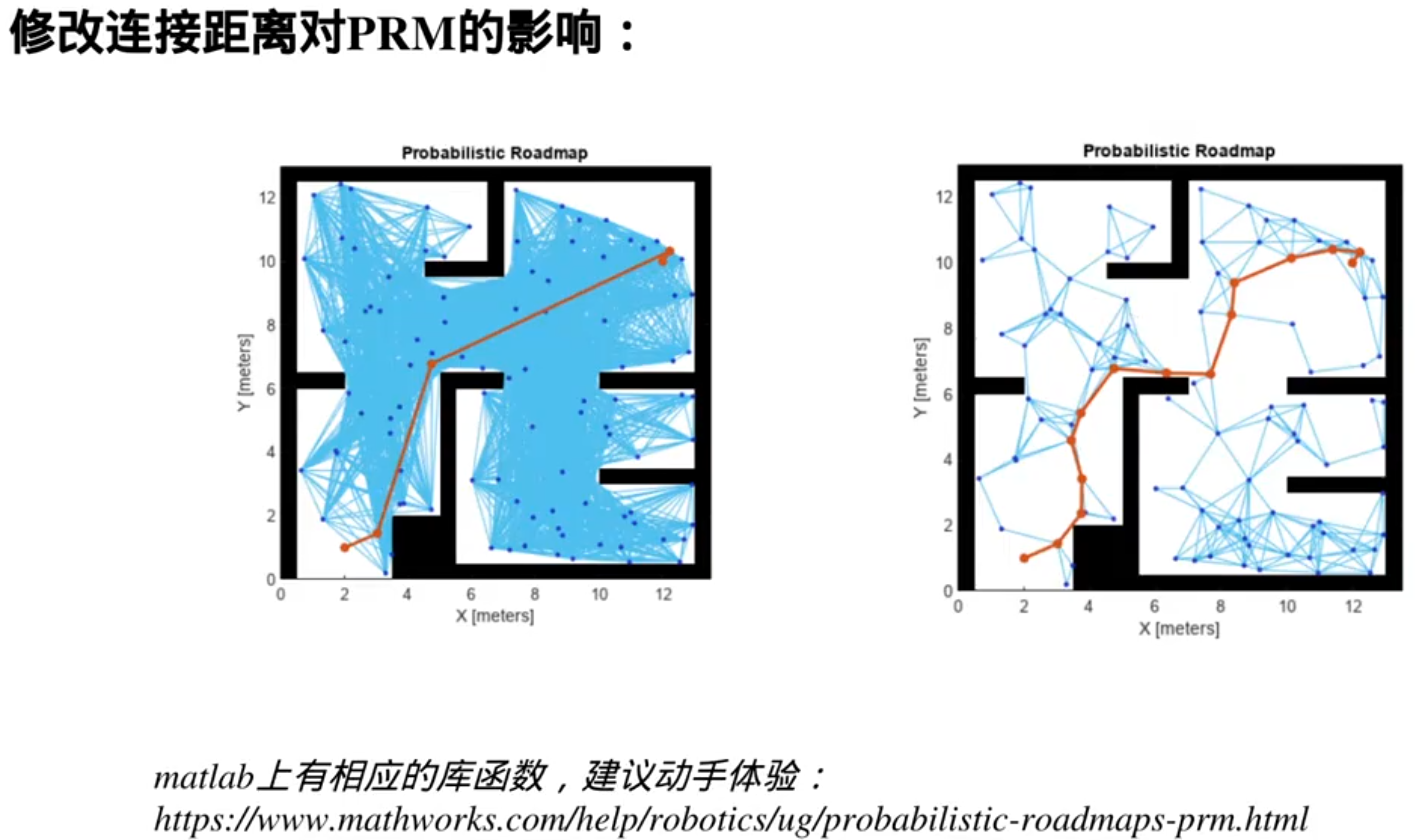
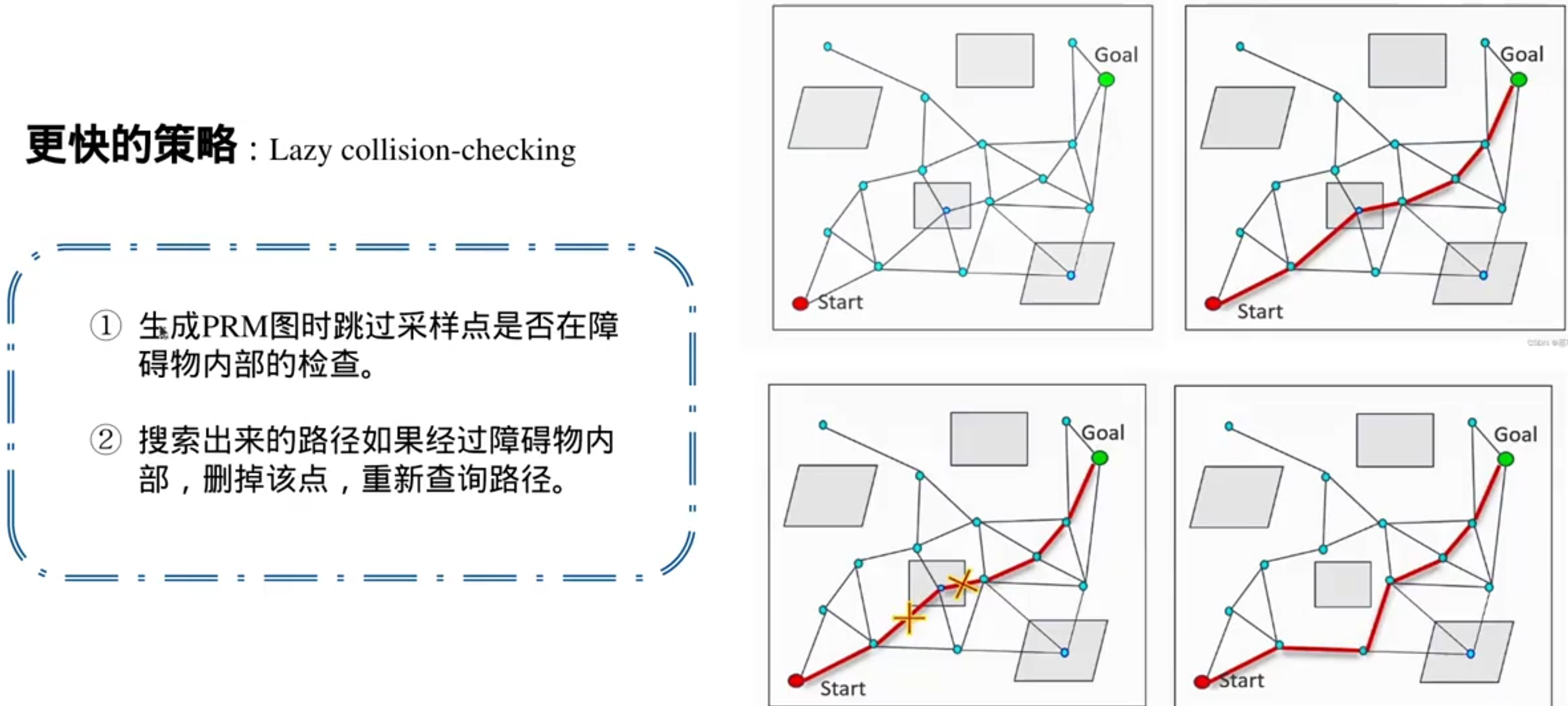
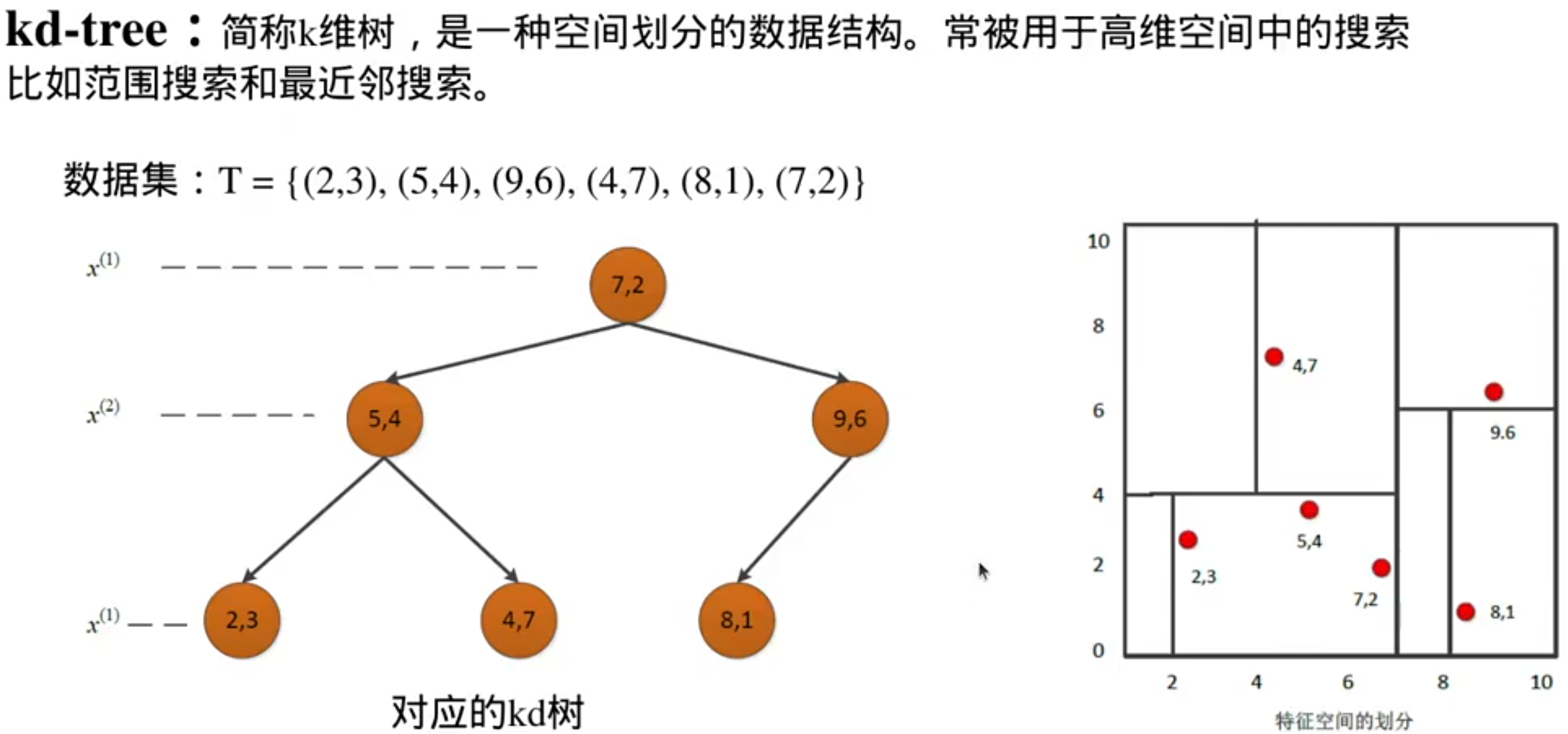
PRM的升级：RRT（快速搜索随机数）

（一边构建地图，一边搜索路径）

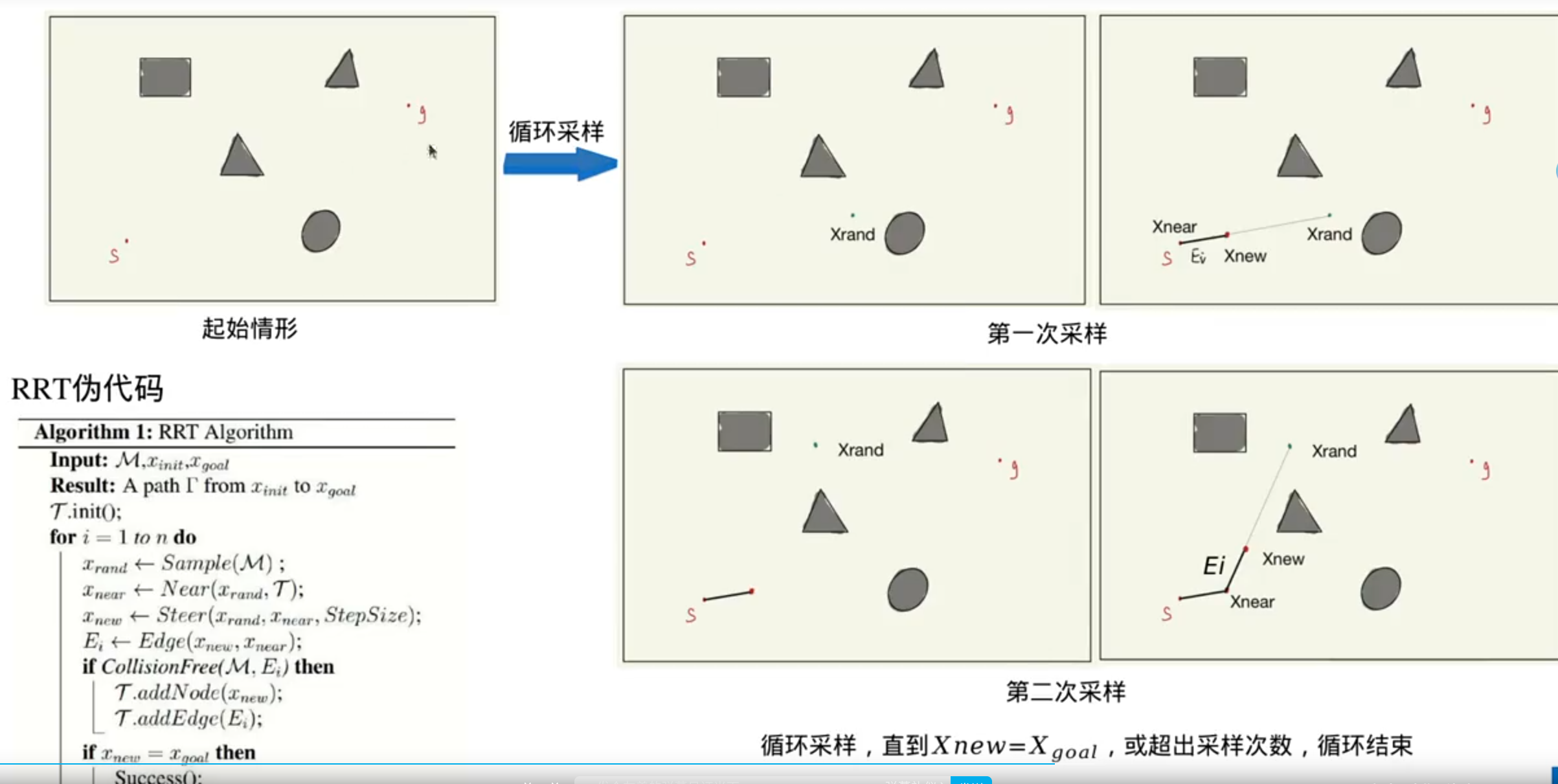
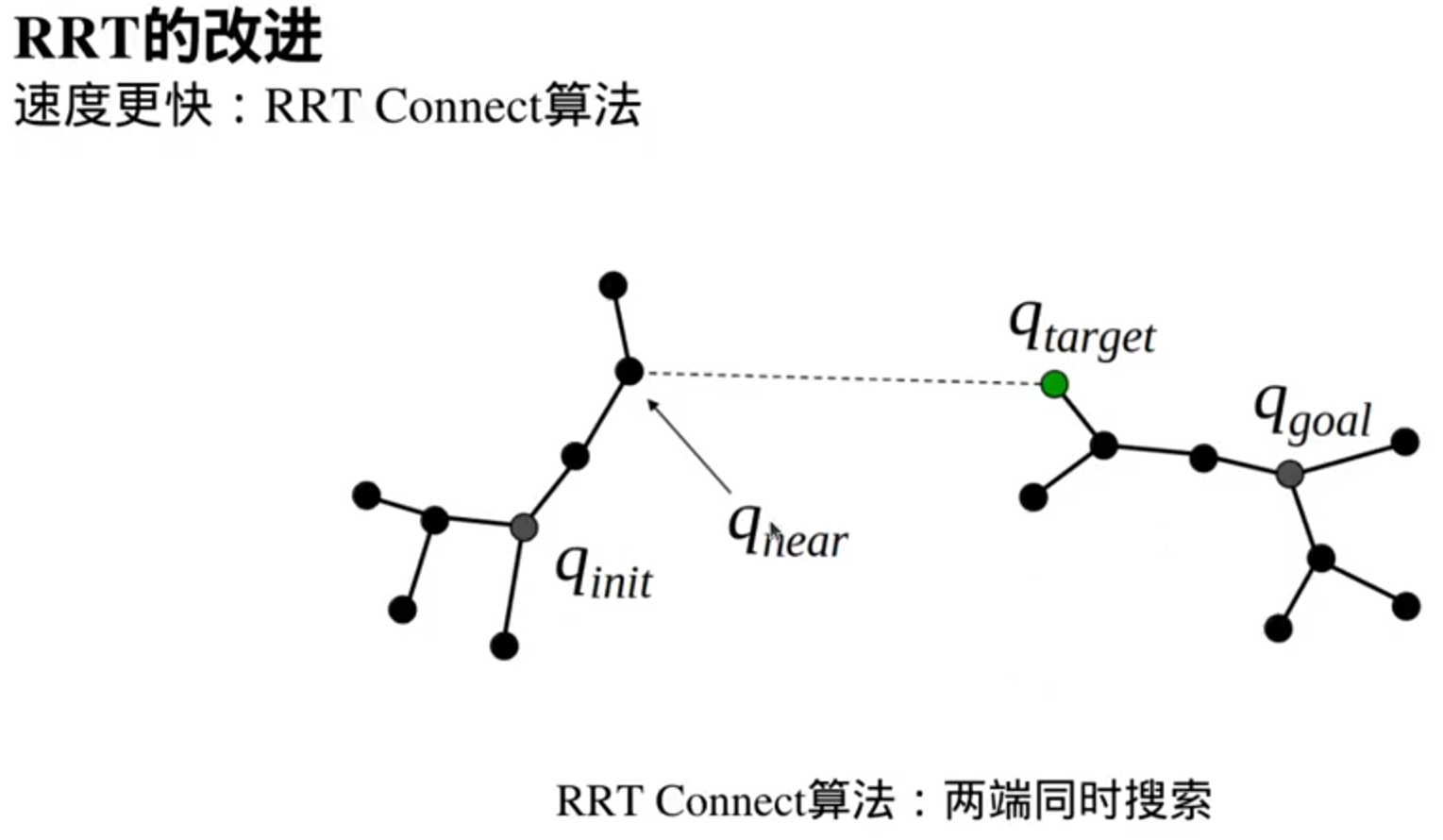
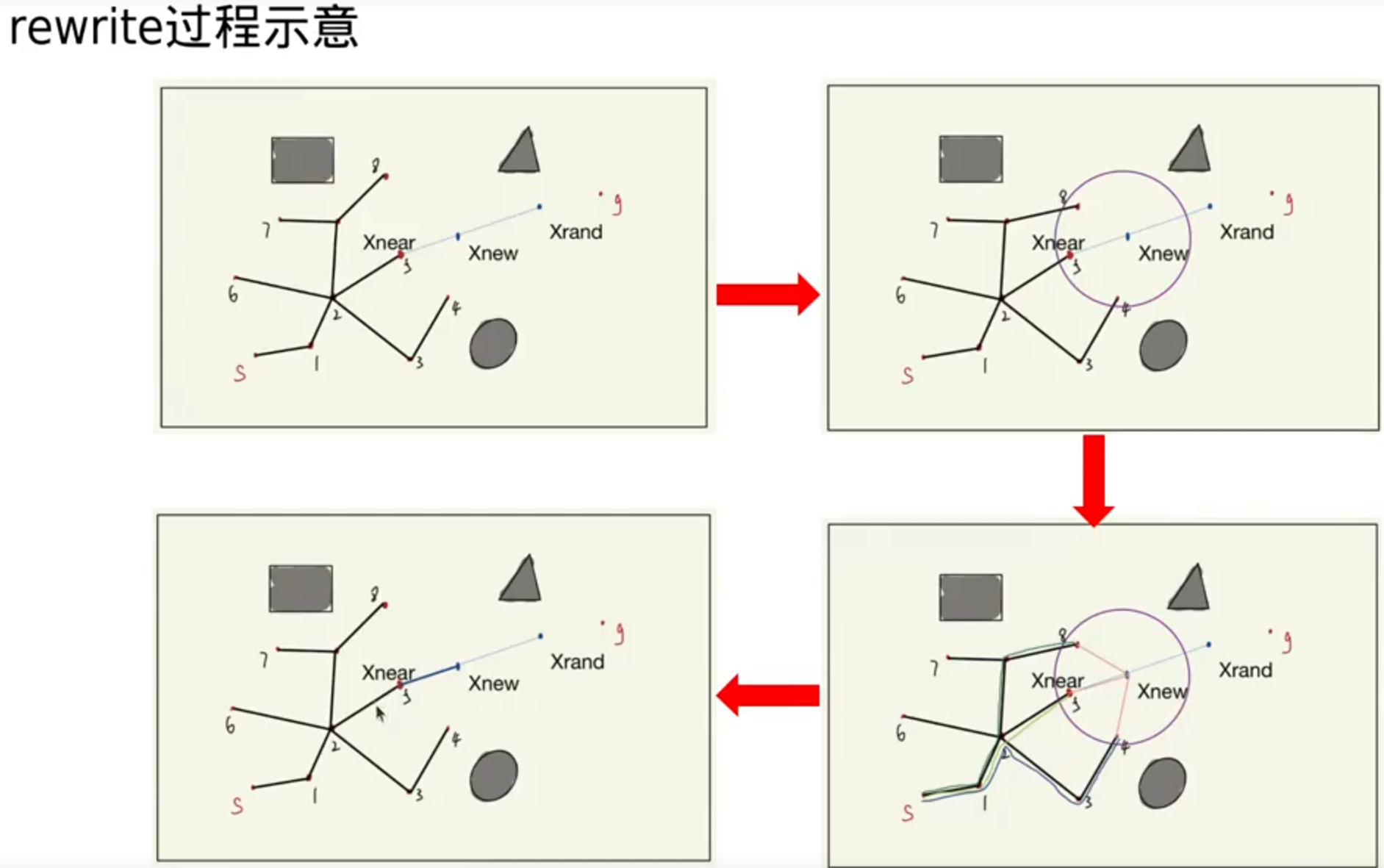
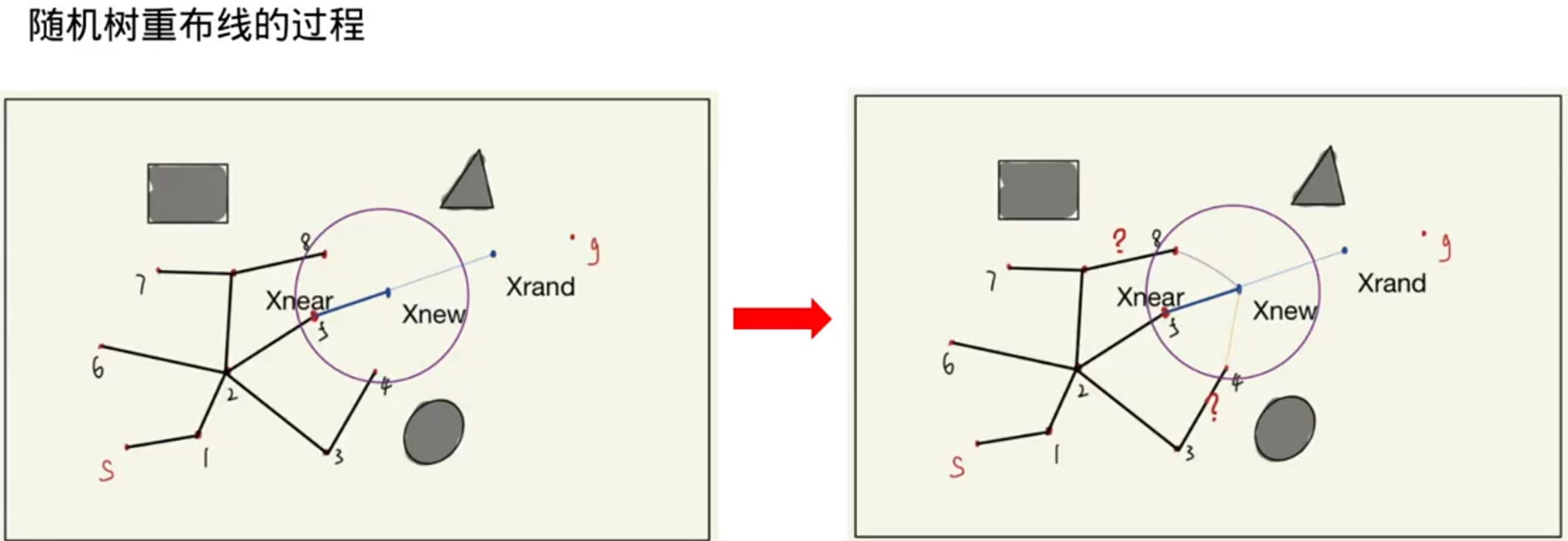
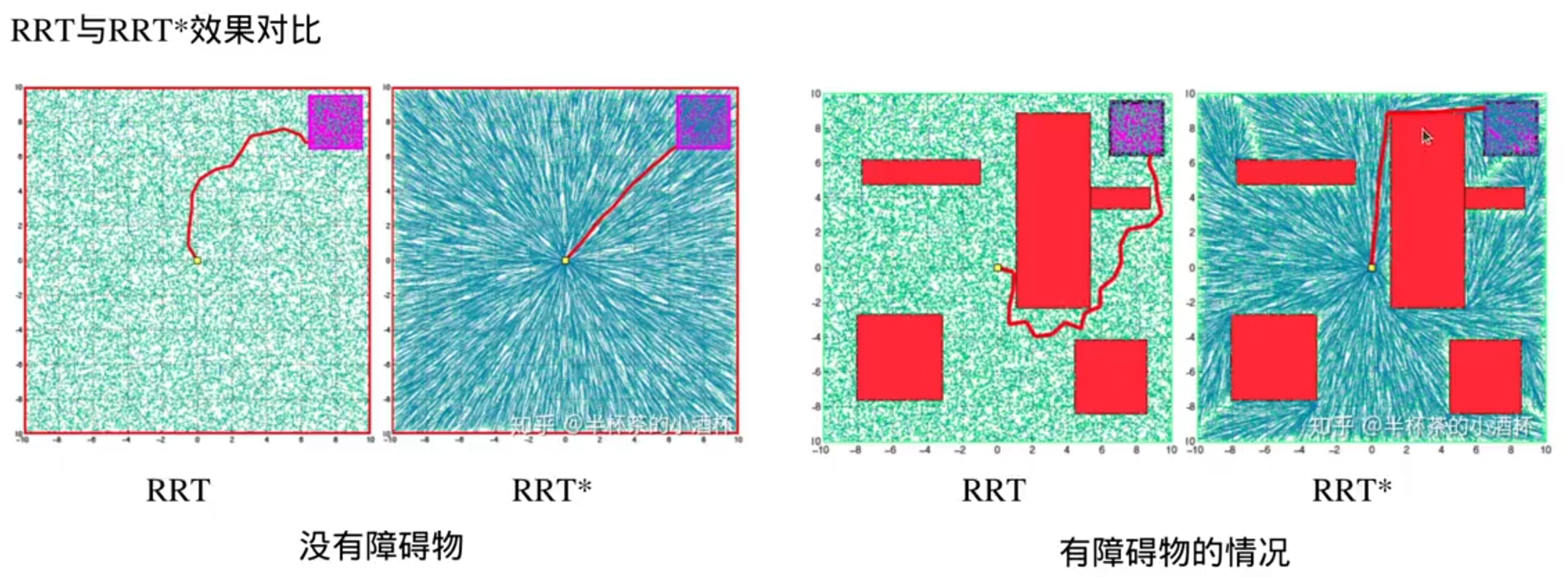
基于图搜索的路径搜索算法

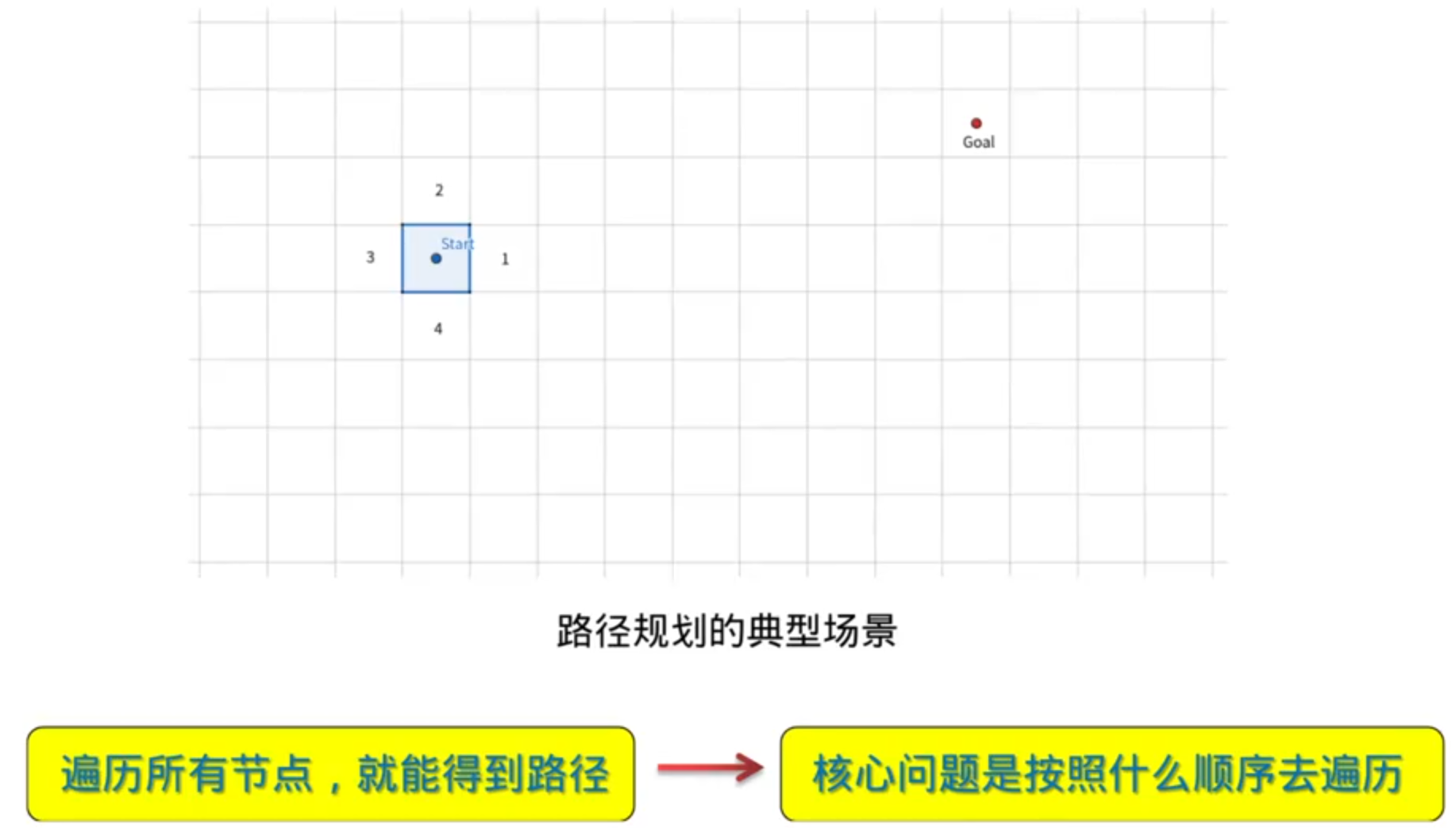
1.朴素的搜索思想——BFS，DFS

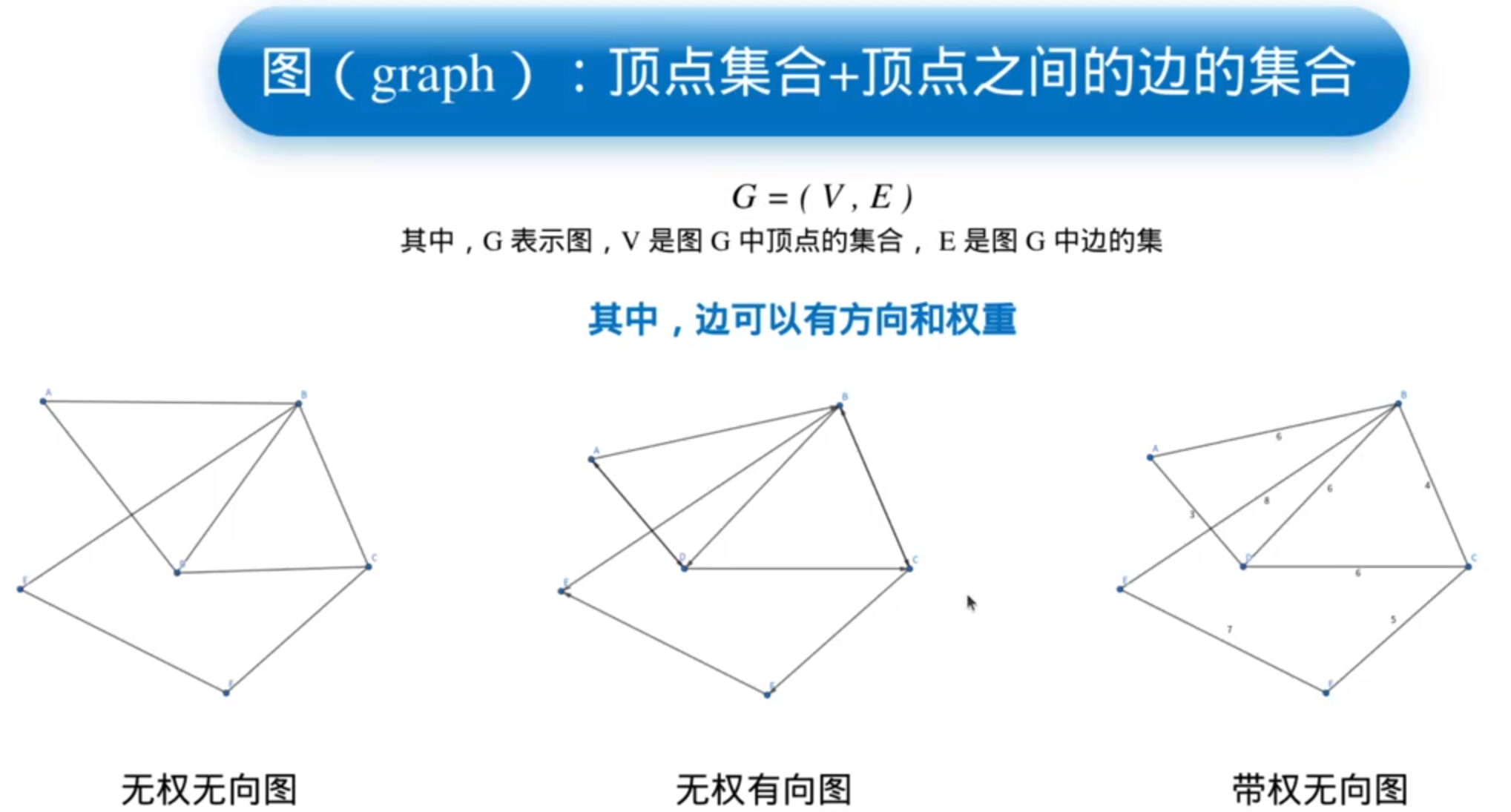
栅格地图可以很容易的转换成graph，欧式距离场可以很容易的转换成栅格地图，拓扑地图本身就是graph

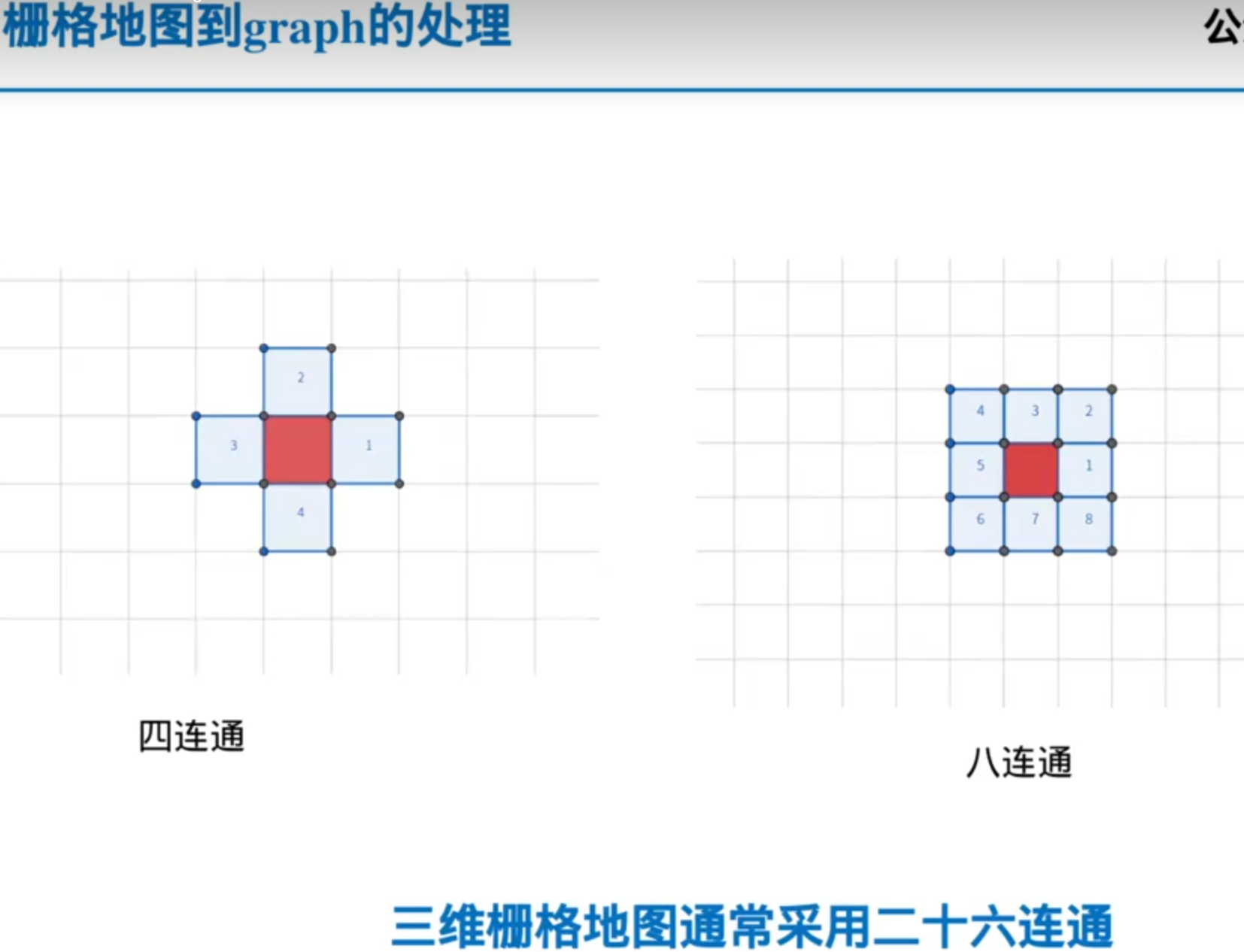
图搜索的核心问题：

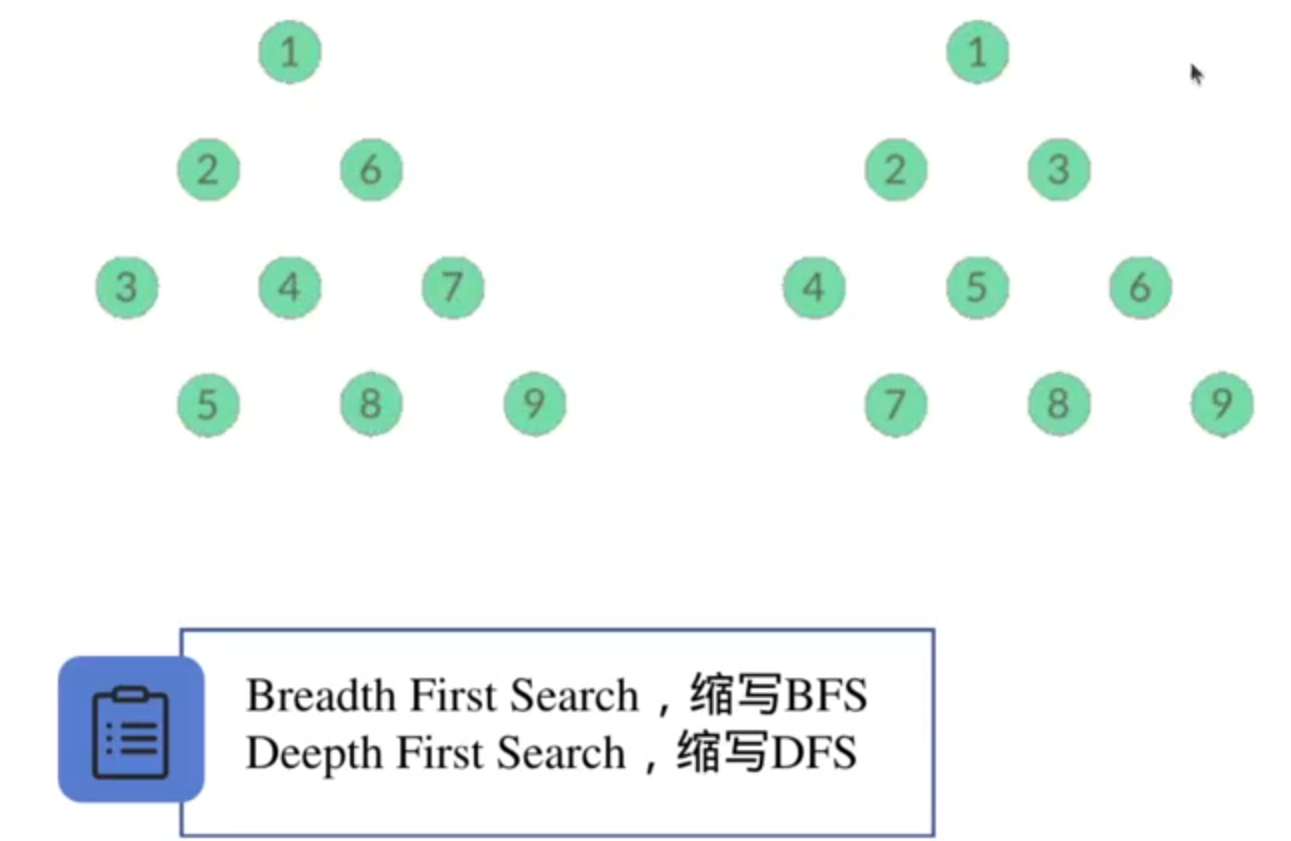
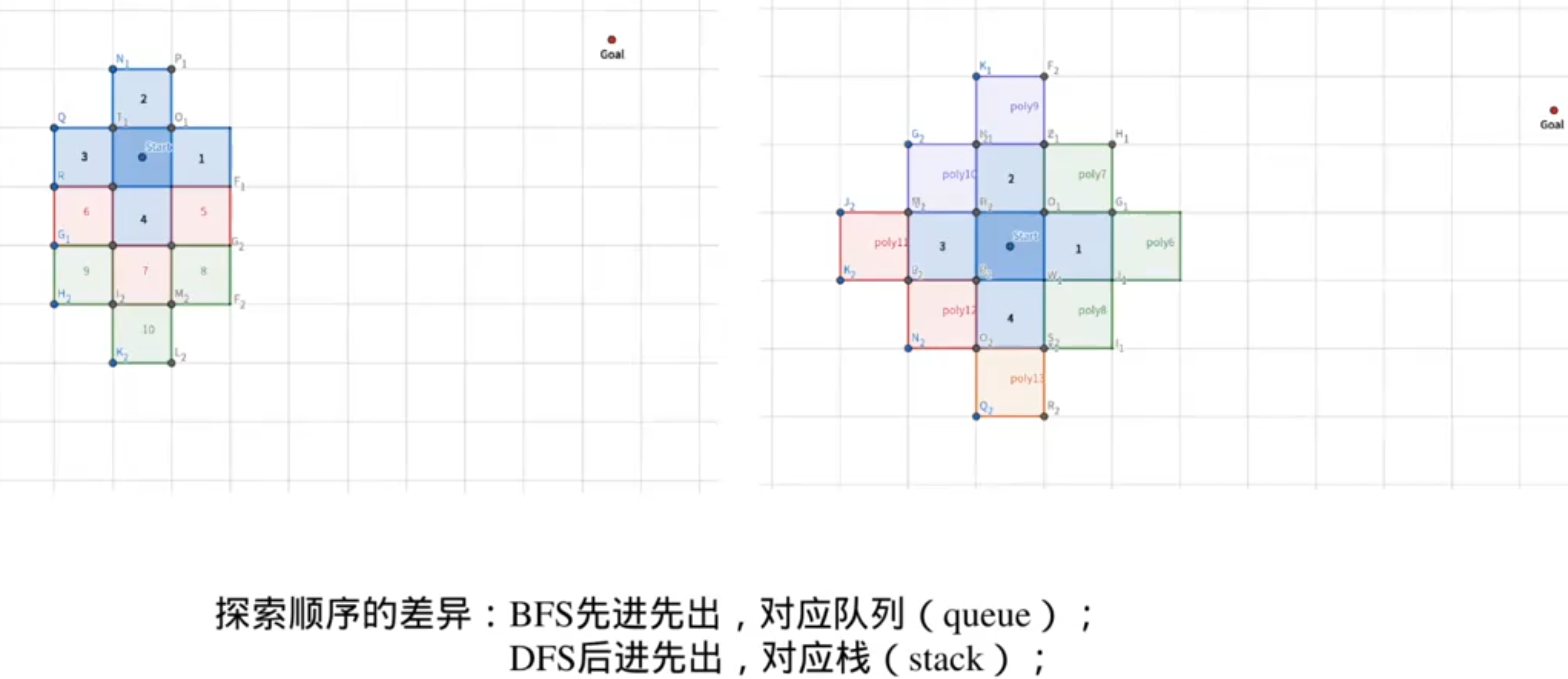
std::reverse 是 C++ 标准库中的一个算法，用于反转给定范围内的元素顺序。它定义在 <algorithm> 头文件中。

std::reverse 接受两个迭代器作为参数，表示要反转的范围。其基本语法如下：

#include <algorithm> // 需要包含这个头文件
#include <vector>
#include <iostream>

int main() {
    std::vector<int> vec = {1, 2, 3, 4, 5};

    // 反转 vec 中的元素
    std::reverse(vec.begin(), vec.end());

    // 输出反转后的结果
    for (int v : vec) {
        std::cout << v << " "; // 输出: 5 4 3 2 1
    }

    return 0;
}

2.（DFS，BFS）搜索算法的进化————Dijkstra,A*

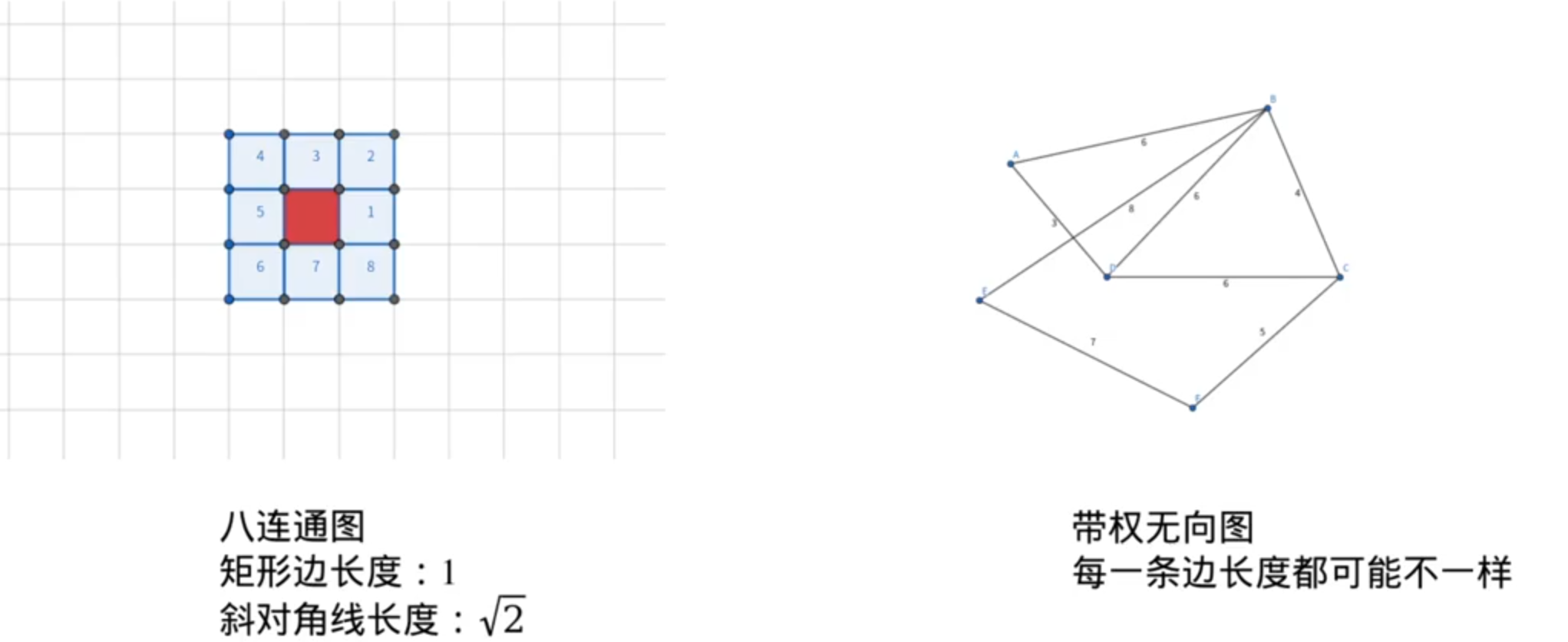
Dijkstra(使用八联通图，可以走斜线)

为什么: 如果distance._current大于distance[current]: 继续下一次循环

- 优先队列会按照节点的最小距离进行排序。可能在多个阶段，一个节点被加入队列，但这些加入可能是基于旧的距离值。
- 当我们从队列中弹出一个节点时，这个节点的距离可能并不是它的最短距离（因为它可能已经被更短的路径更新过）。
- 如果当前弹出的节点的距离大于我们在 distance 数组中记录的最短距离，这意味着我们已经找到了一条更短的路径到达这个节点，因此可以跳过对这个节点的处理。

A*（优化搜索速度）

A*的核心思想：不但考虑七点到当前节点的代价值，还要考虑当前节点到目标点的代价值

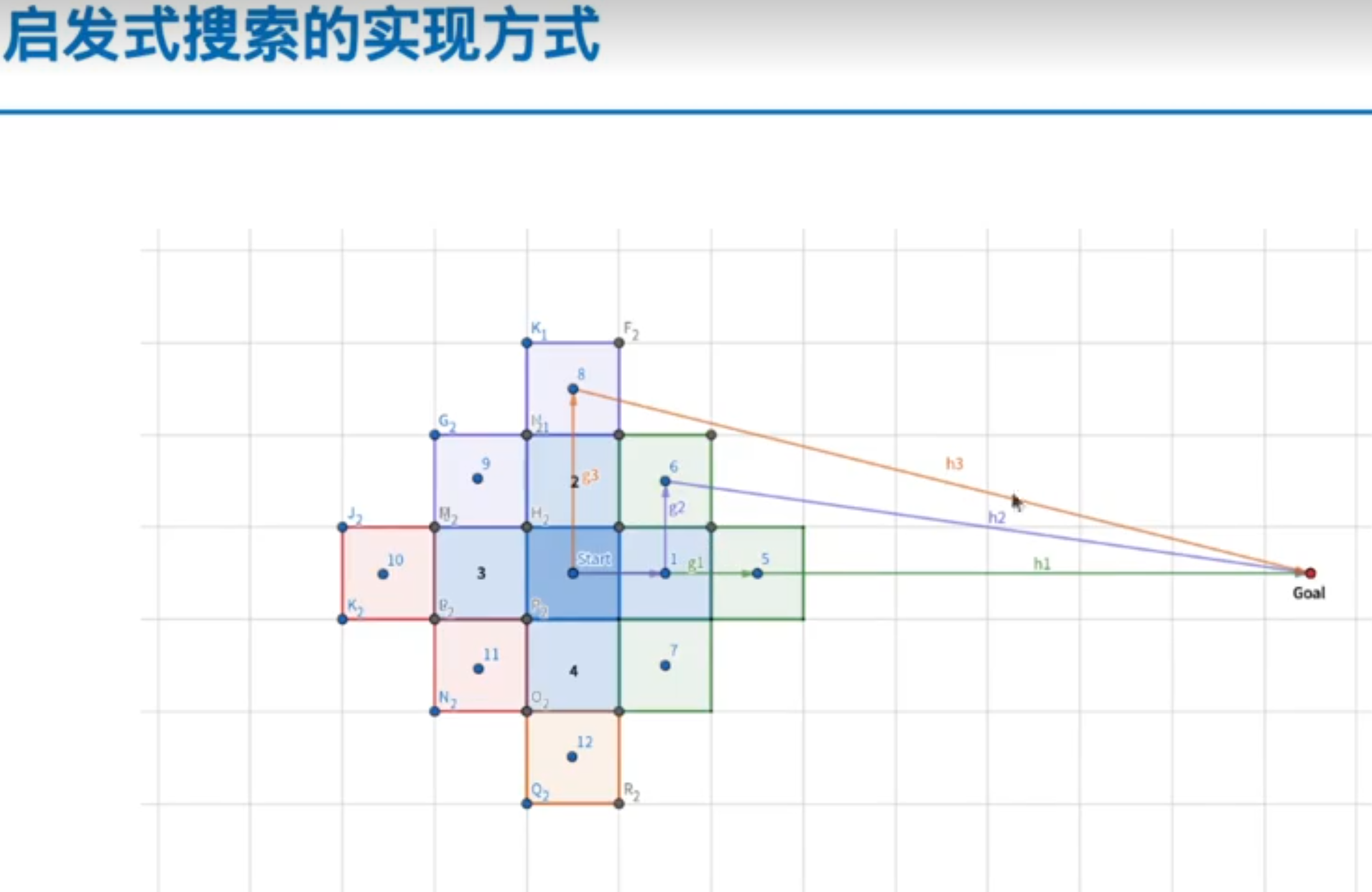
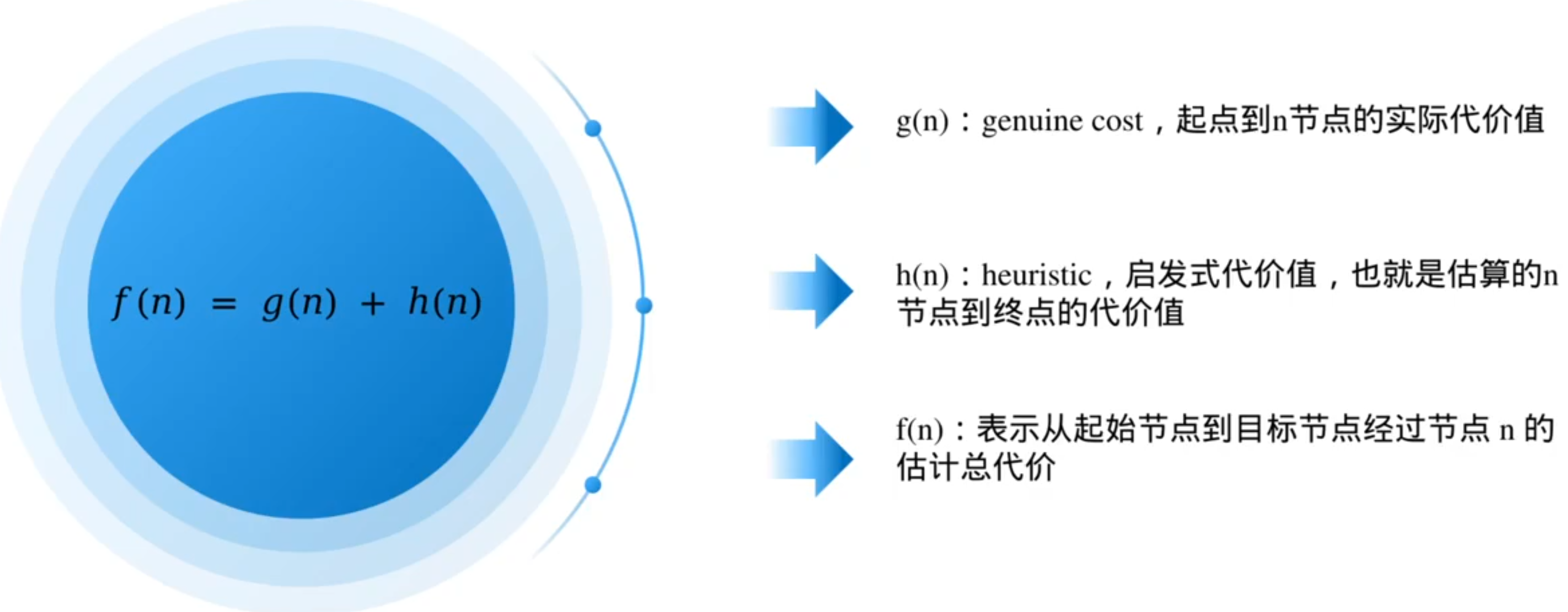
这里的估算函数叫启发式函数

常用的启发式函数

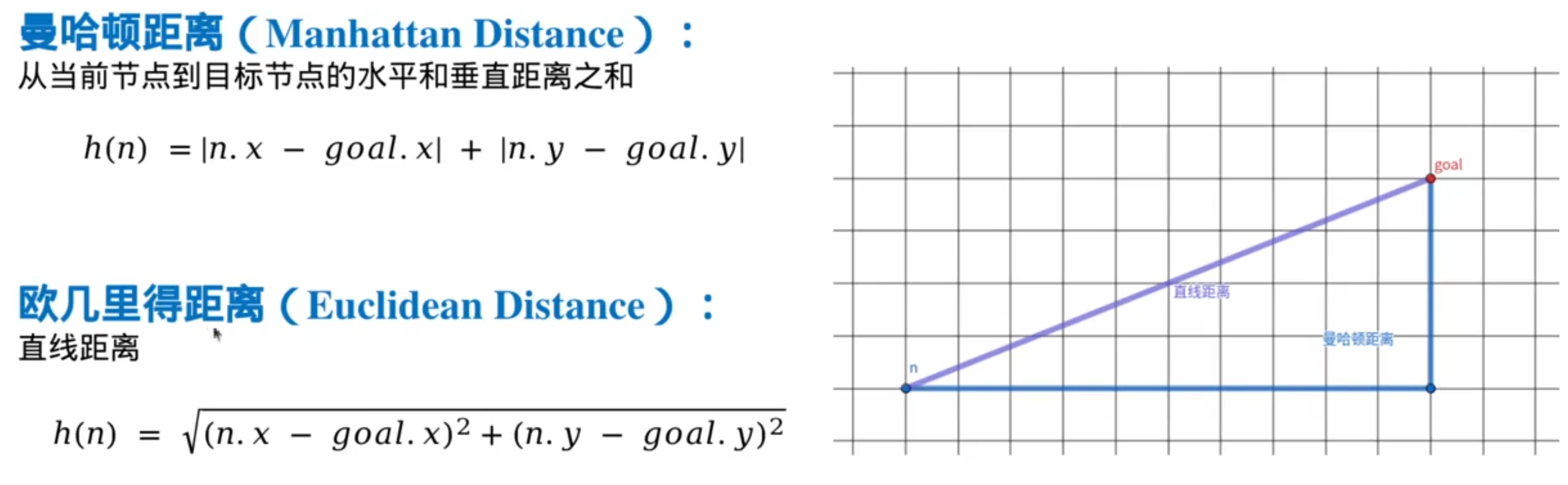
注意：曼哈顿距离>真实距离（有可能无法保证路径最优）,但就因为它比较大，所以有时候它的效果最好

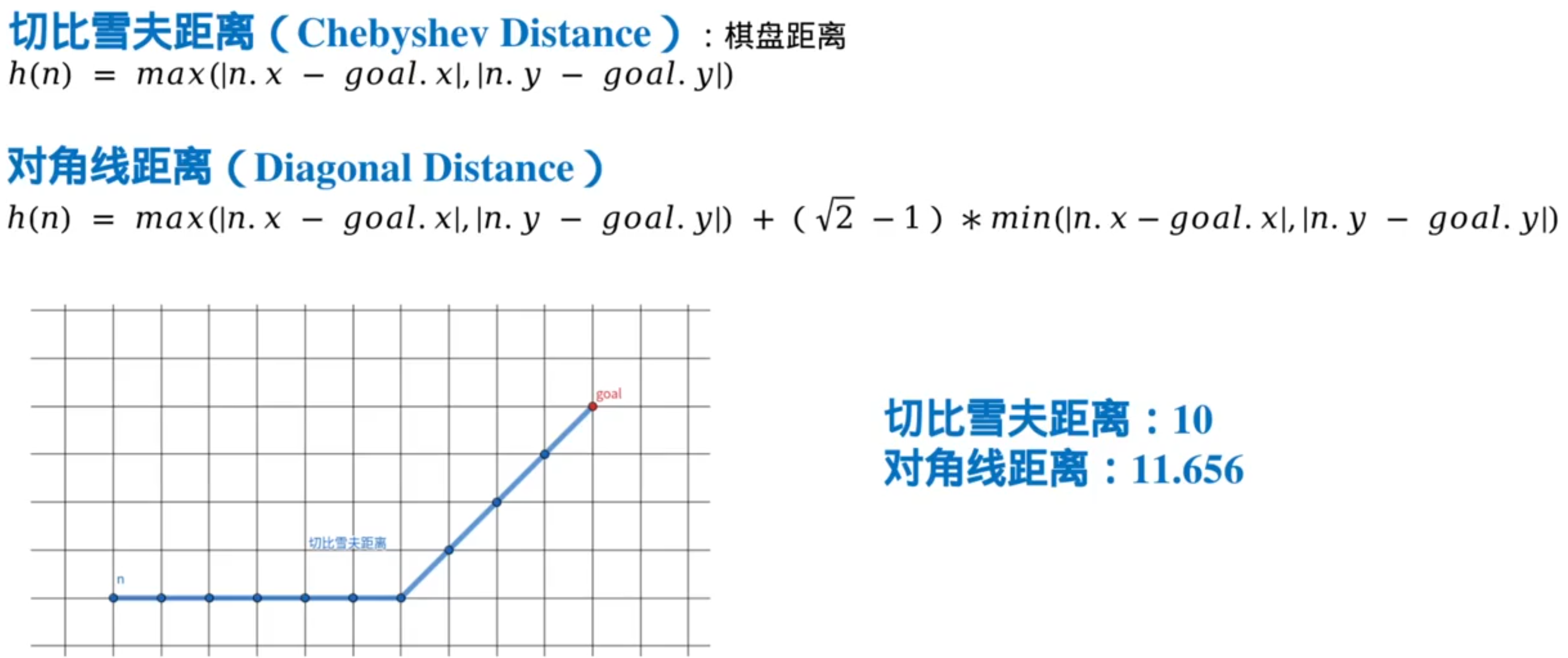
A*算法的最优性保证：

只有满足条件，A*所得的路径才是最短路径

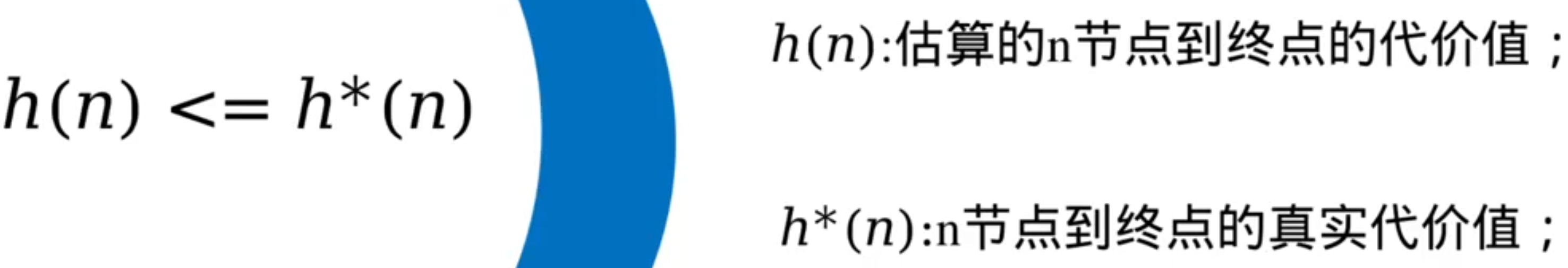
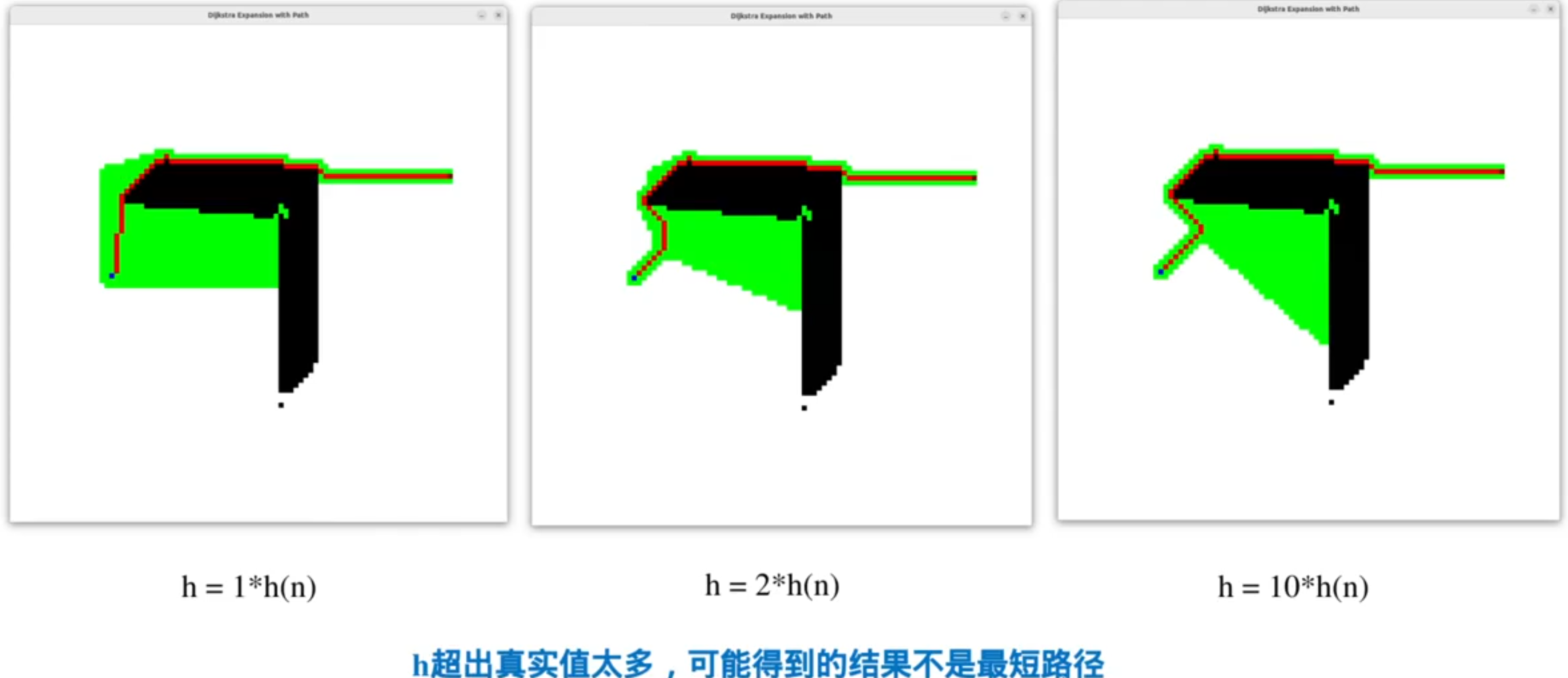
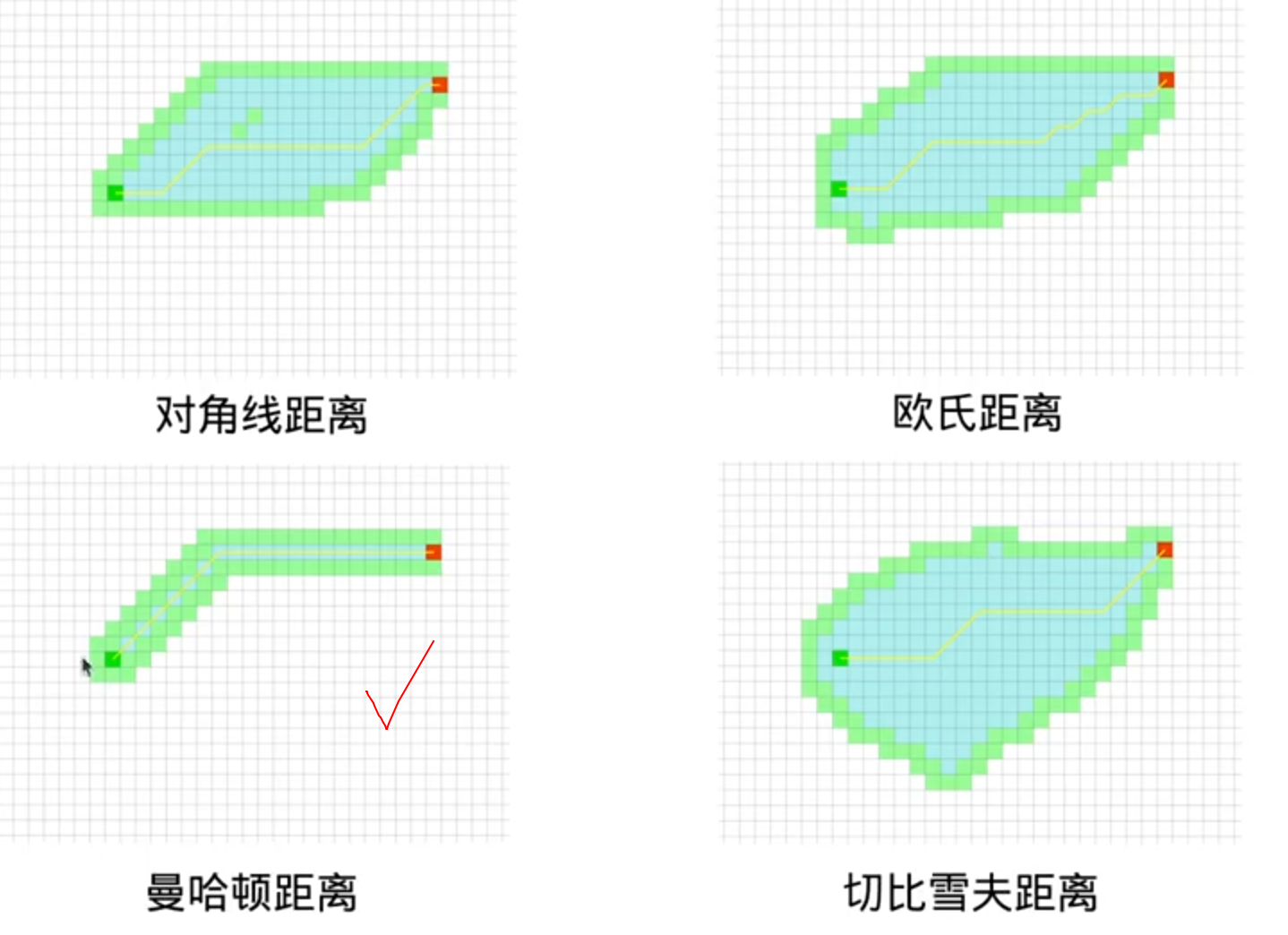
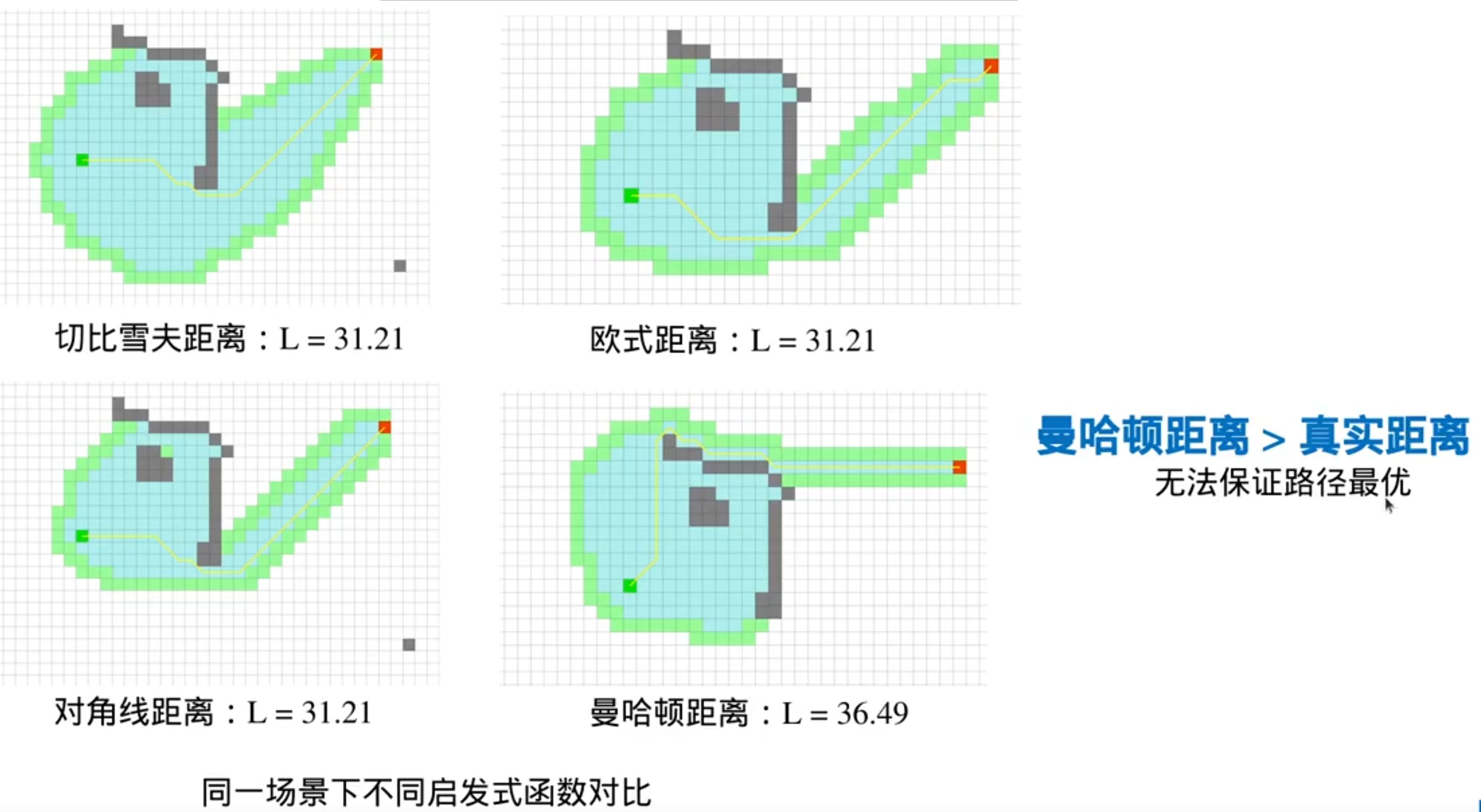
启发函数的选择：

A*的平衡性问题：

虽然A* 算法的结果和理想结果的路径都是最短的，但是理想结果的转折更少，更适合使用，而且A* 算法搜索的节点还是有点多

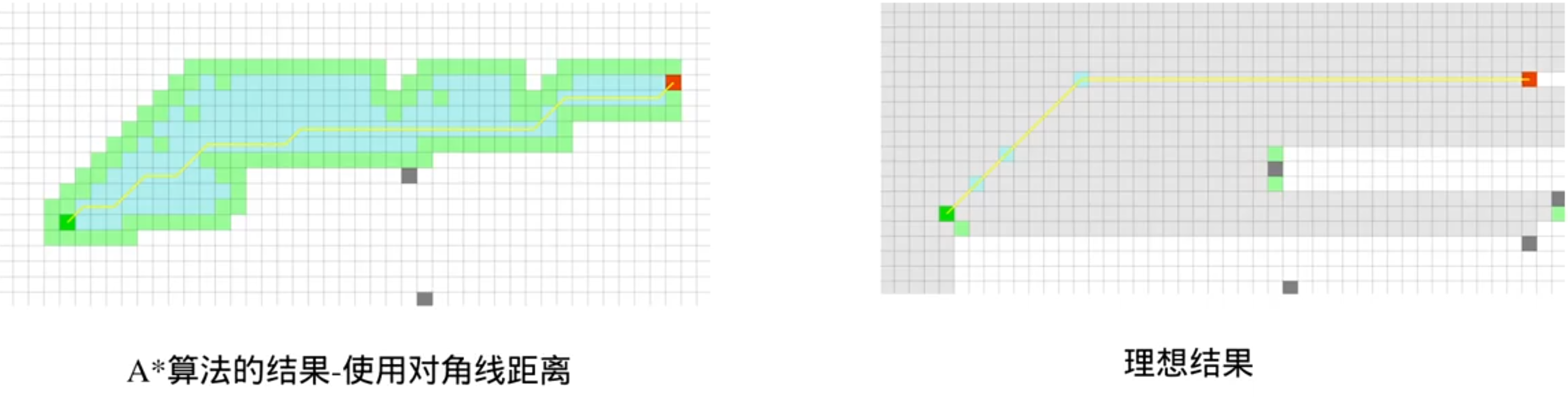
怎么解决呢？

从Dijkstra到A *增加了一个指标，效果大大提升，那再加一个指标

在实际工程上，DFS会用递归方法实现

一种有趣的搜索思路：JPS

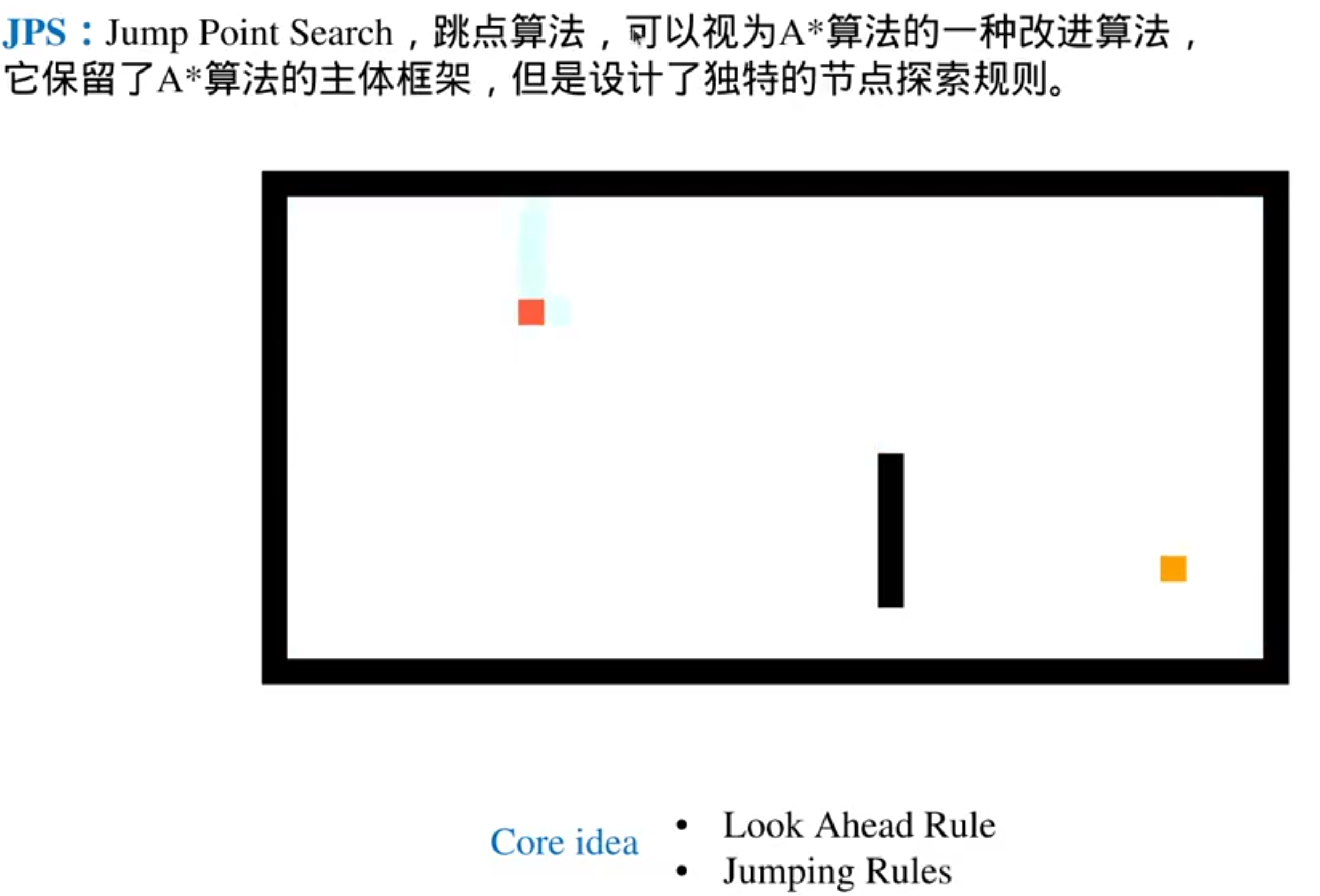
JPS是一种跳跃式搜索算法：关注障碍物边缘的关键性节点（最短路径是起点+障碍物边缘节点+终点）

解决A *算法的平衡性问题

强迫邻居是必须要探索的点（强迫邻居有可能就是绕过障碍物的关键节点）

跳点和强迫邻居都需要继续拓展，所以都要加到openlist里面

这就是向前看规则：

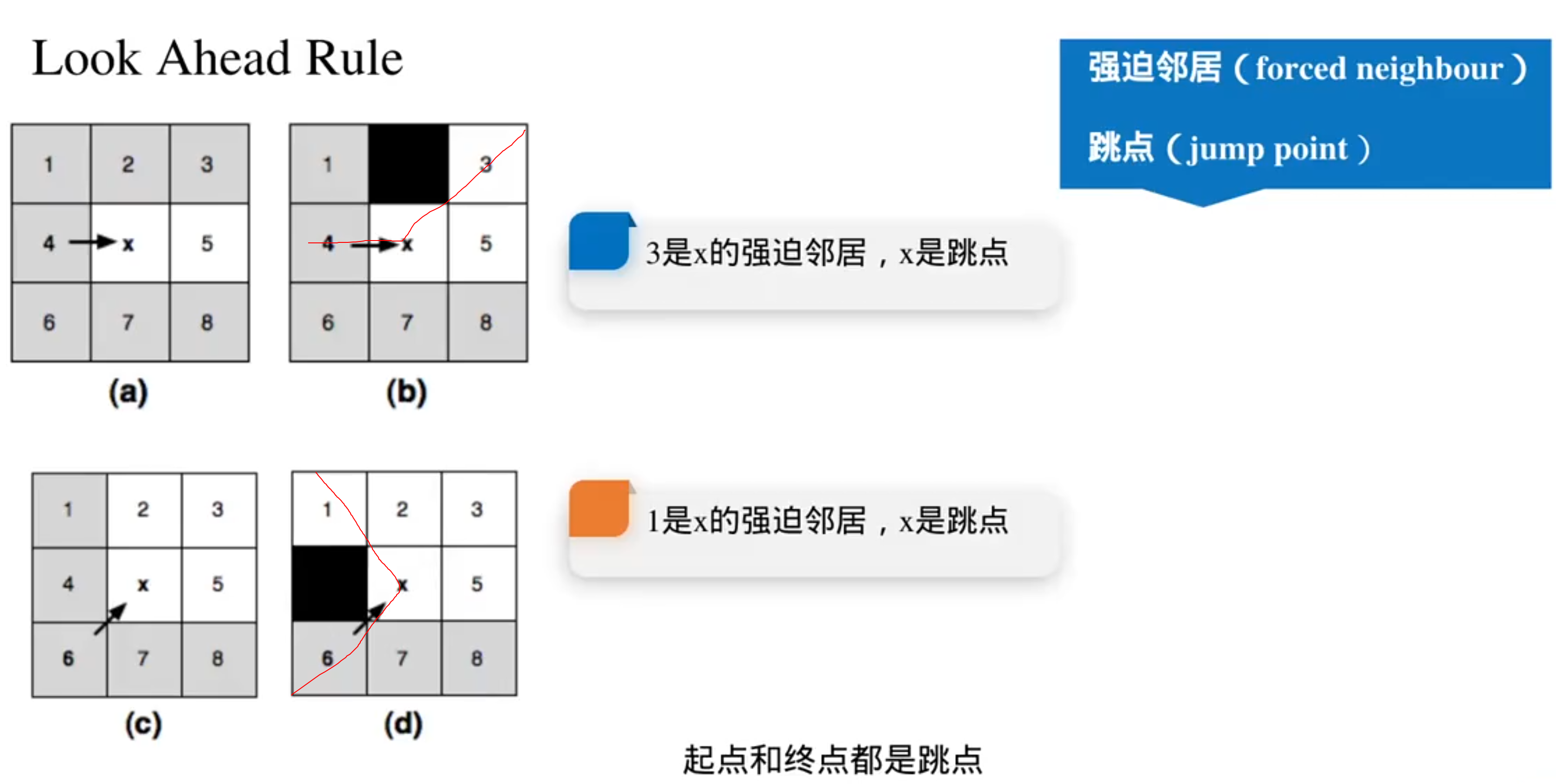
跳跃规则：

起点的八个邻居都需要加入到openlist里，都需要拓展

八邻域探索方向可分为正向和对角线方向

A*会八个方向一圈一圈的探索，JPS是只沿一个方向探索：

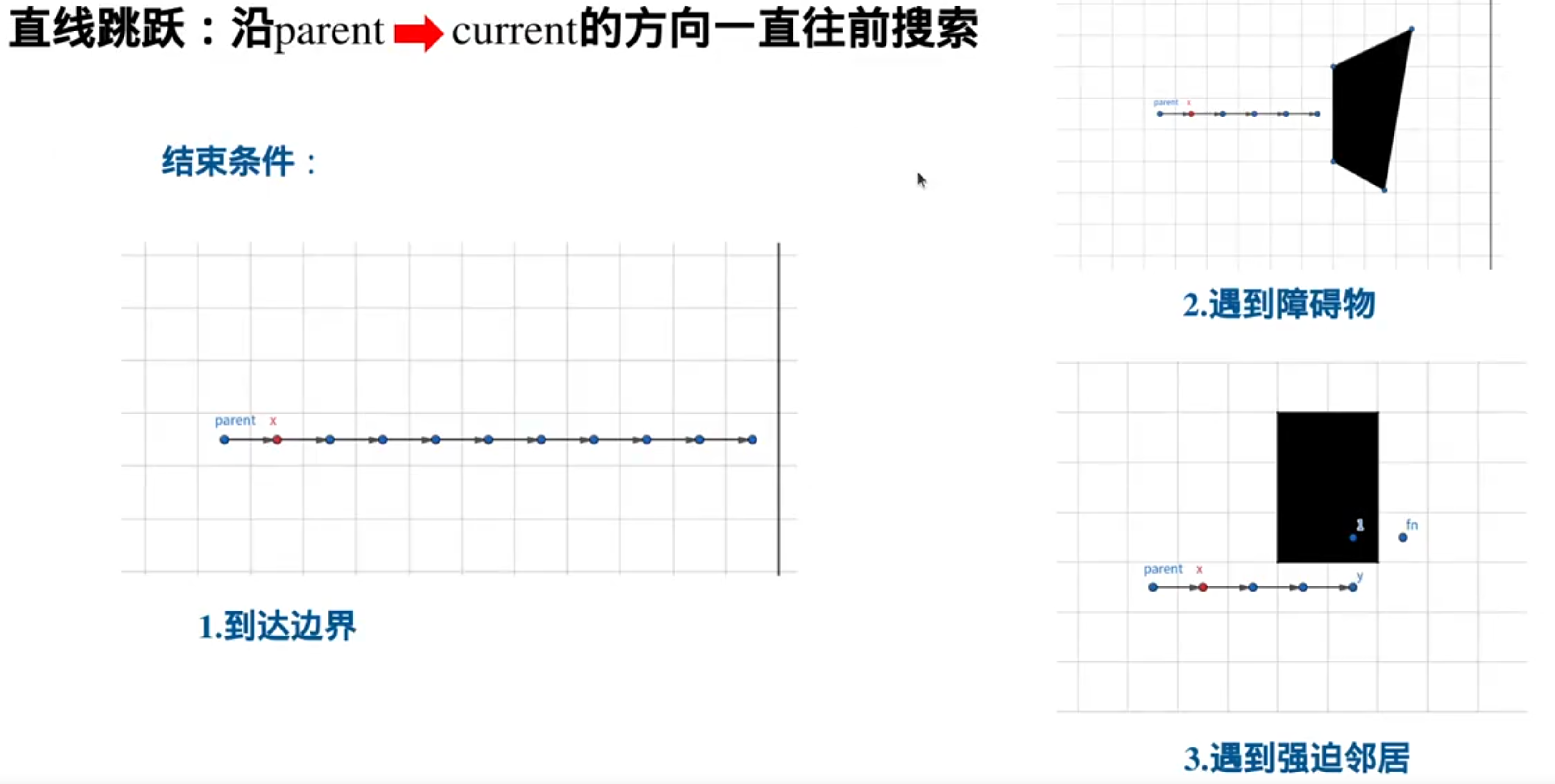
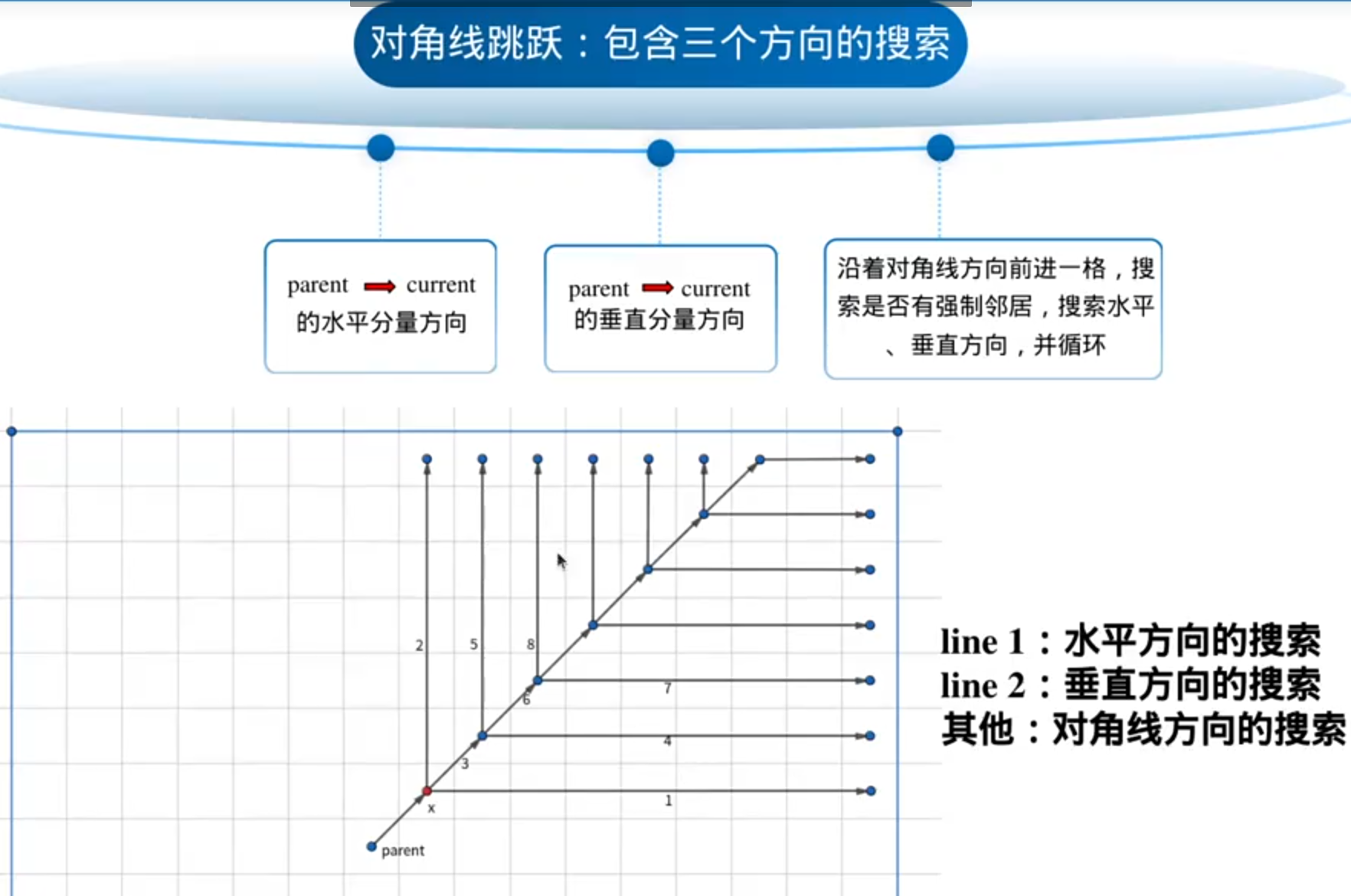
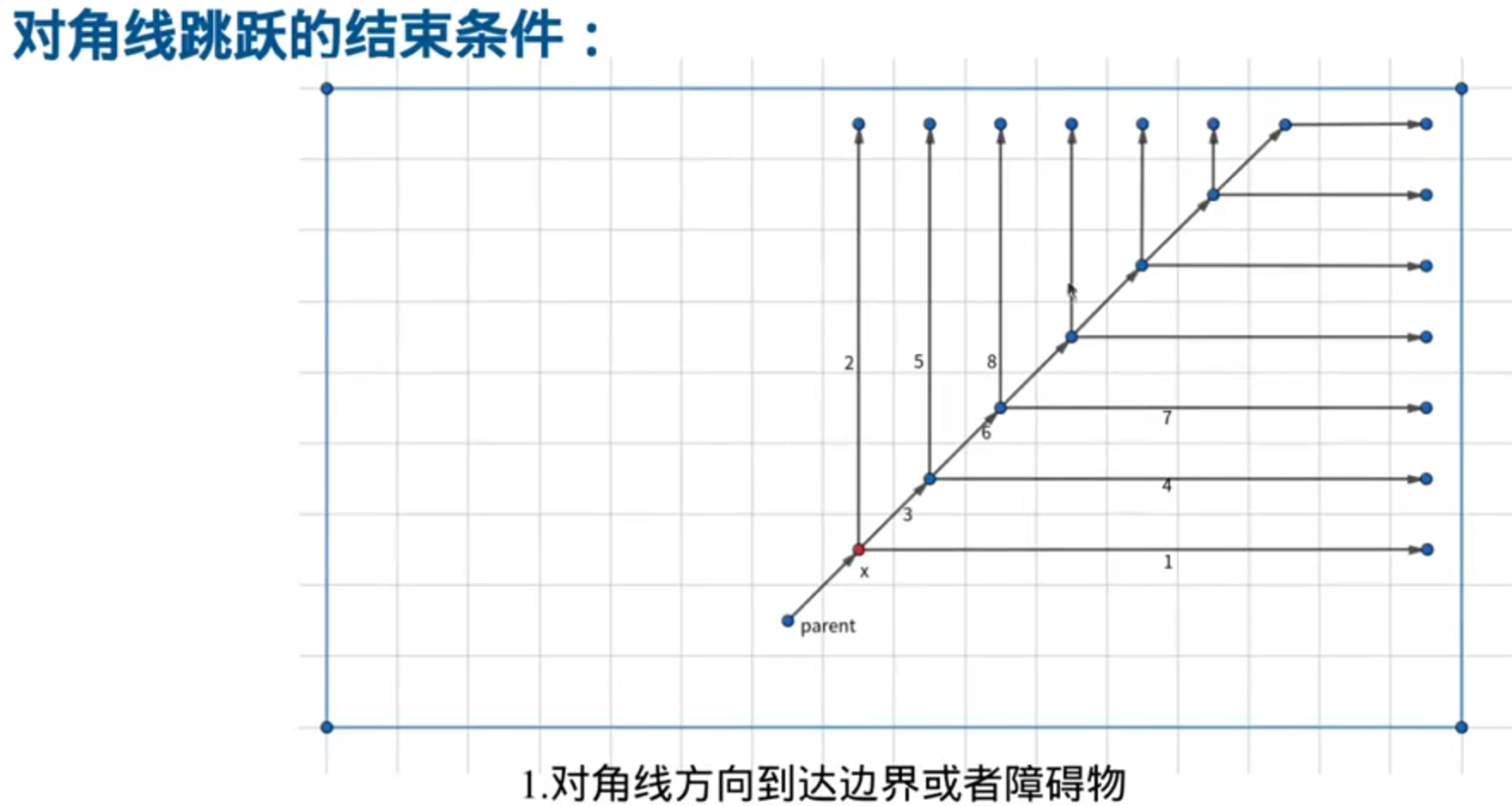
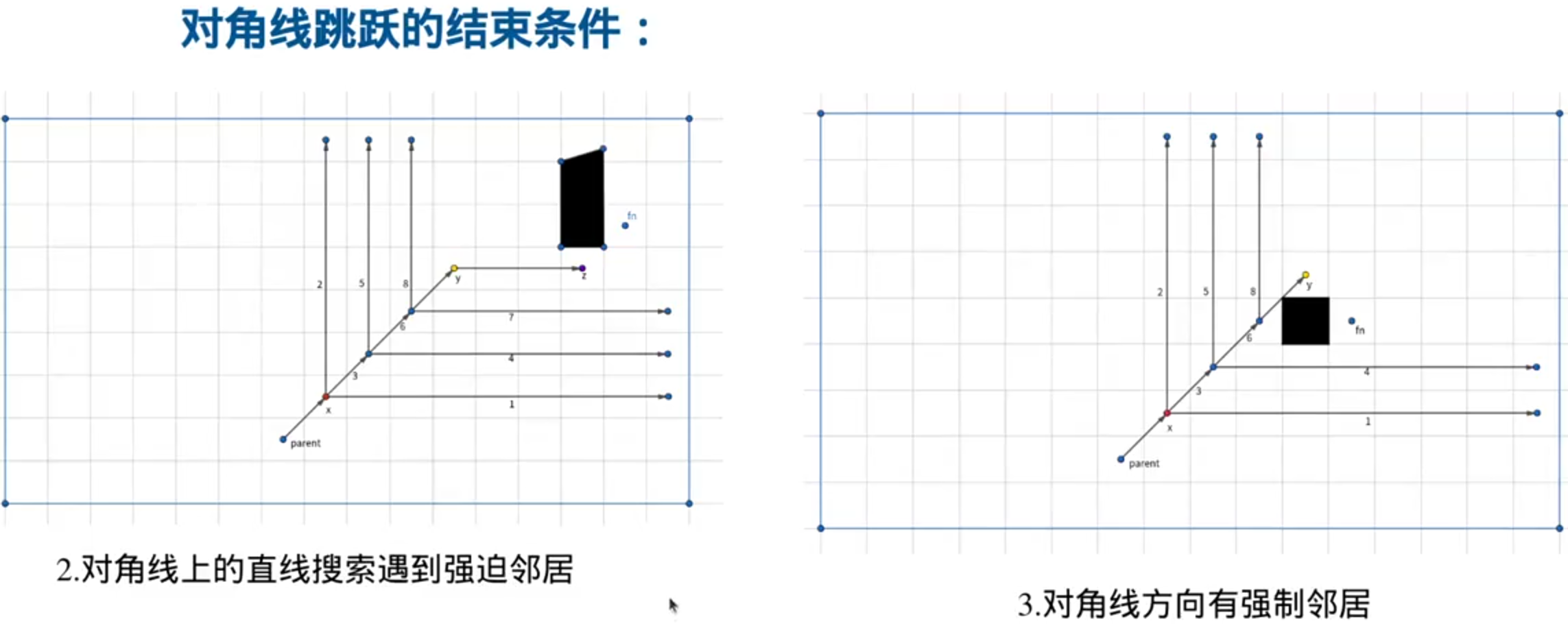
对比：

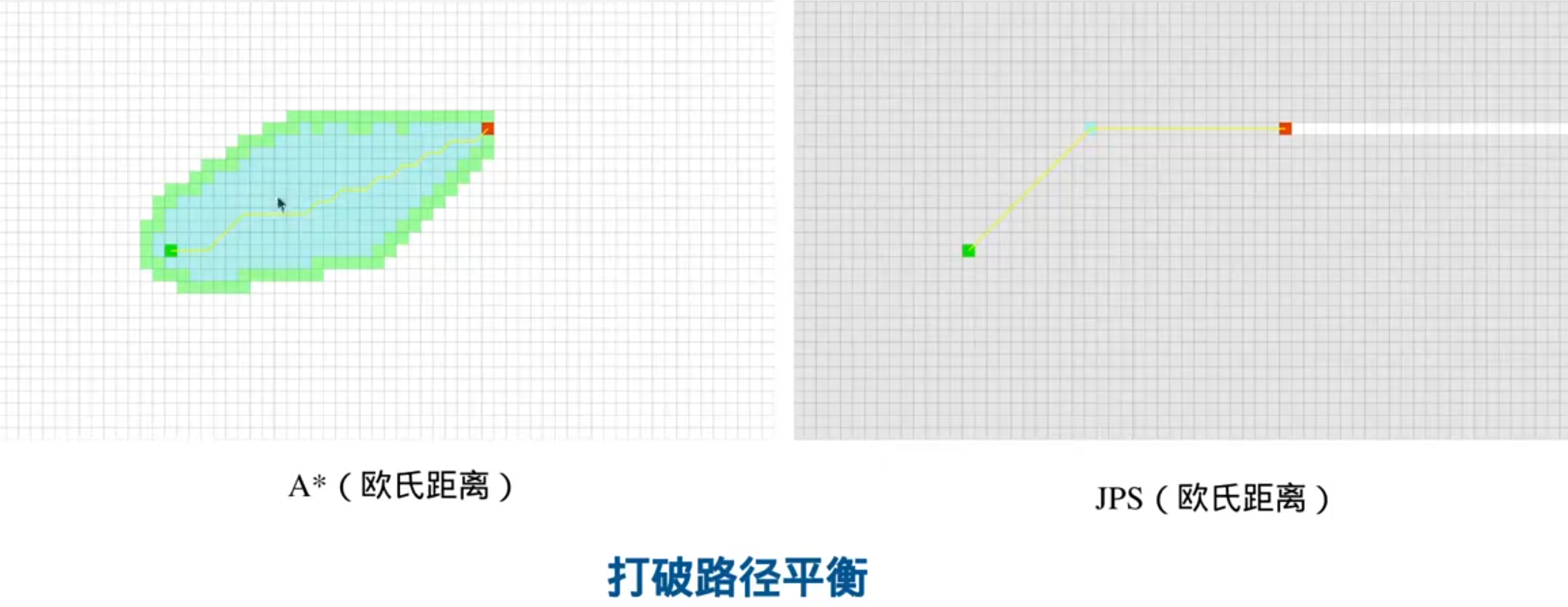
蓝色是被拓展过并添加到openlist里的，绿色是没有拓展过但是添加到openlist里的，右图里灰色是访问过的点

A*的openlist里的节点更多

从容应对动态障碍物–D*（动态A星算法）

D* 又称Dynamic A*

初始生成一条最优路径，在跟踪过程中，根据障碍物的变化，实时调整受影响的局部局部路径

算法流程：

1.方向构建：

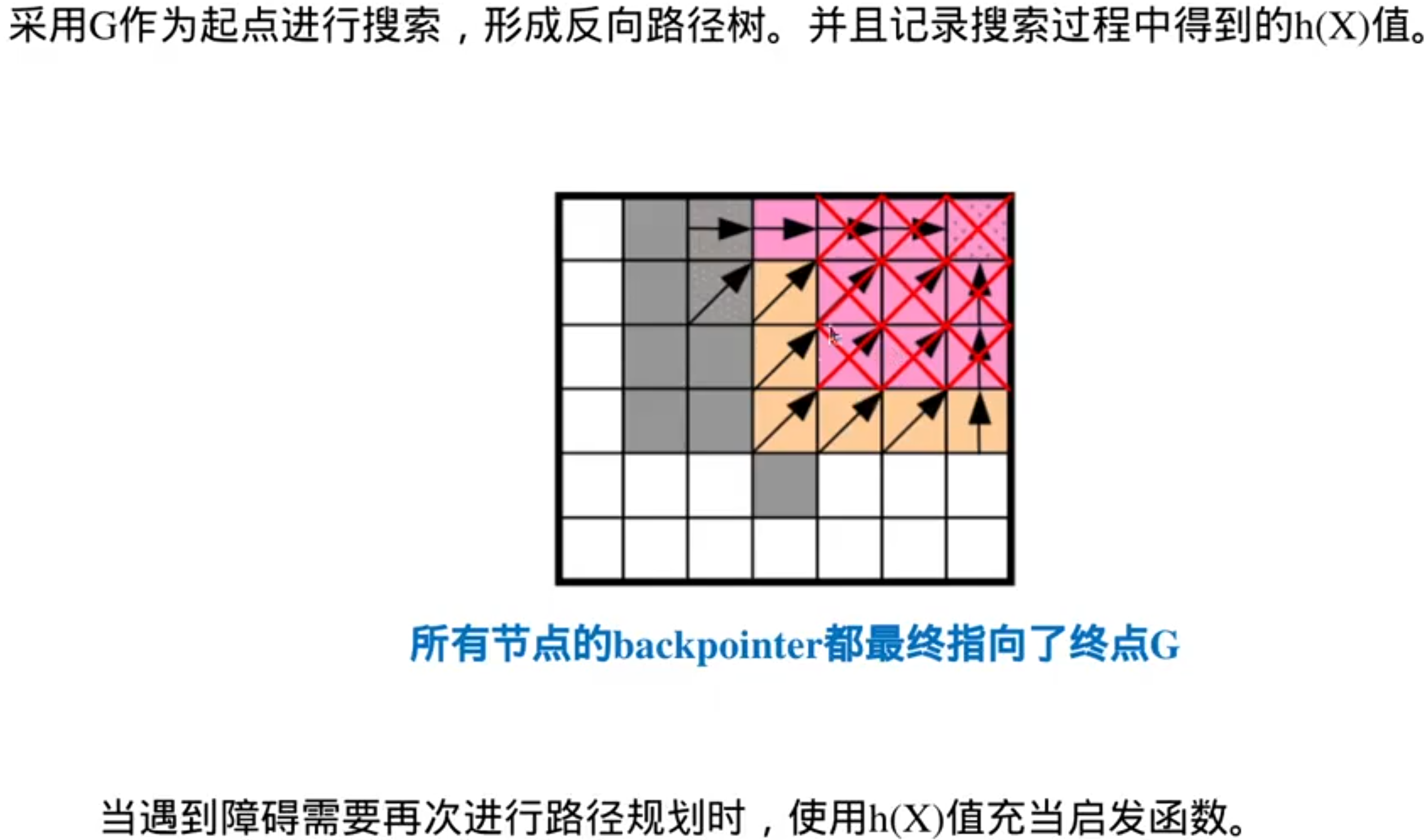
h(X)：用来存储路径代价，指从X到达终点G的路径（{X,……G}，简记为{X}）代价，不一定是全局最优，第一次搜索到起点时时，所有点的h会被更新，计算方式同Dijkstra算法，是用相邻两点的代价+上一个点的代价累加得到

k(X)：用来记录自X节点被加入到OPEN_LIST中后的最小h(X)值（具体计算方式由Insert函数决定）,也是优先队列OPEN_LIST的排序依据，k将会保持到最小，它表示了本点在全图环境中到G点的最小代价(k(x)没有受到障碍物增加的影响)

3，代价修改：

4，状态处理

考虑动力学和运动学的路径搜索

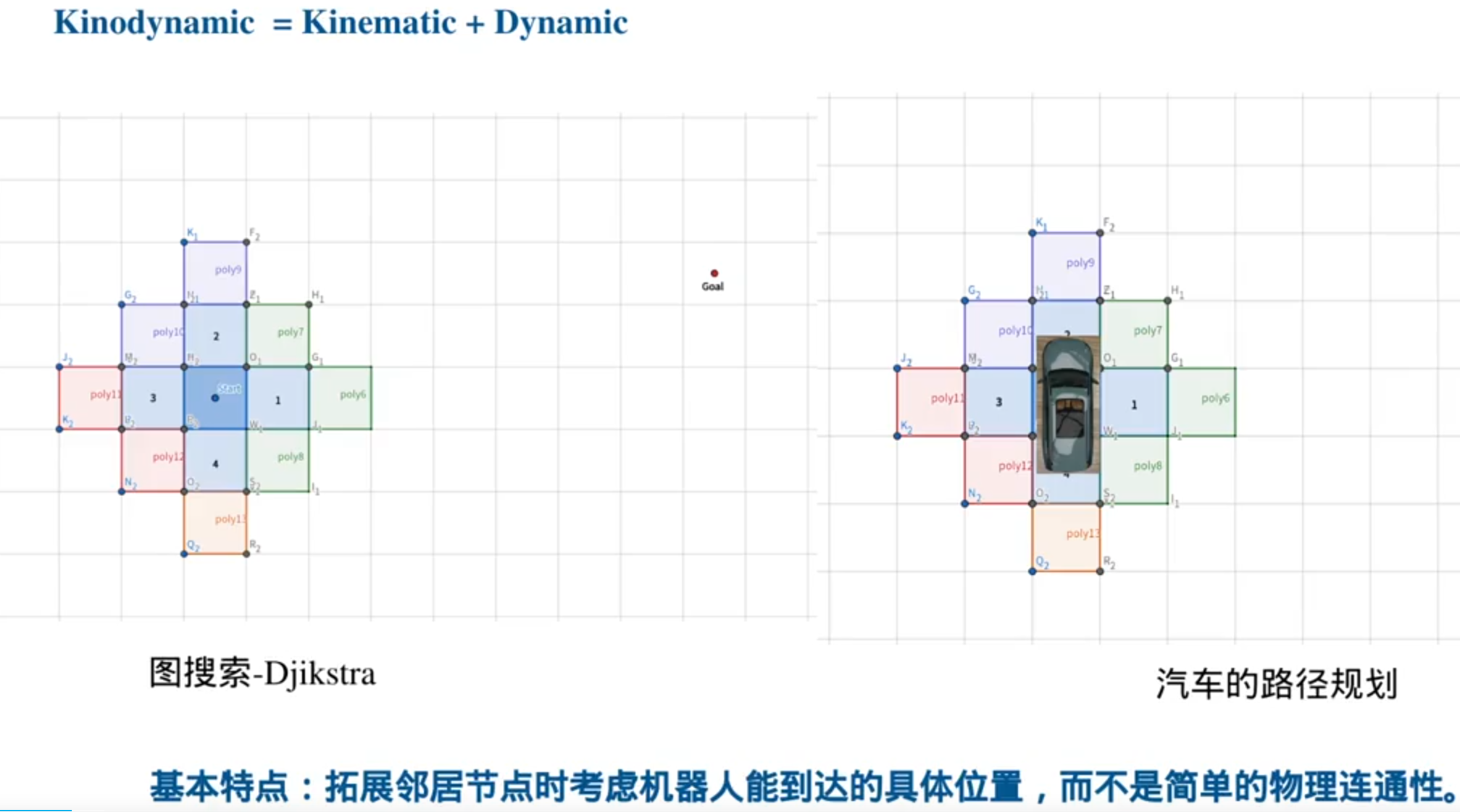
优化了节点的扩展方式，节点不一定是栅格的中心(弧形路径)

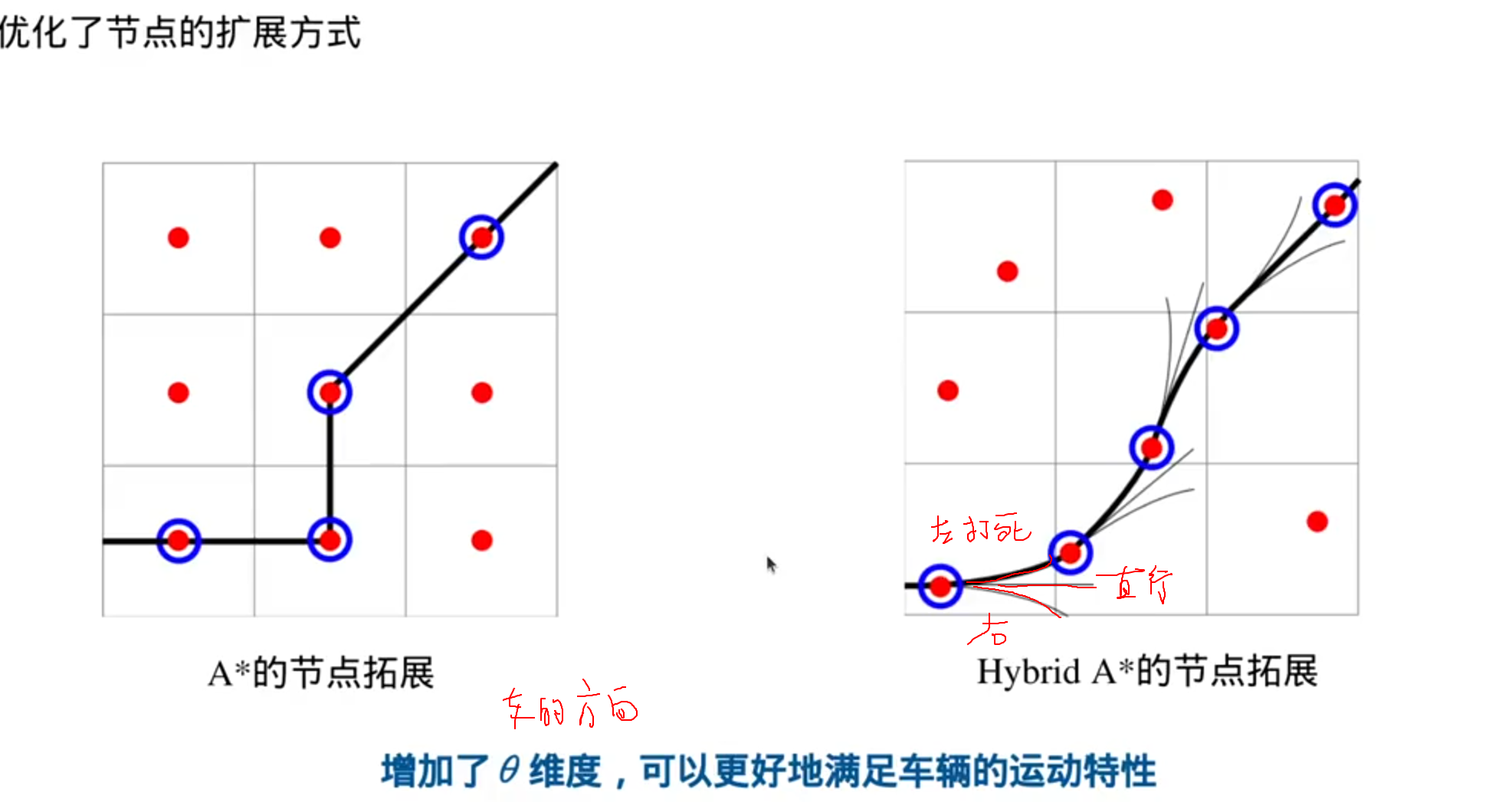
优化了启发式函数

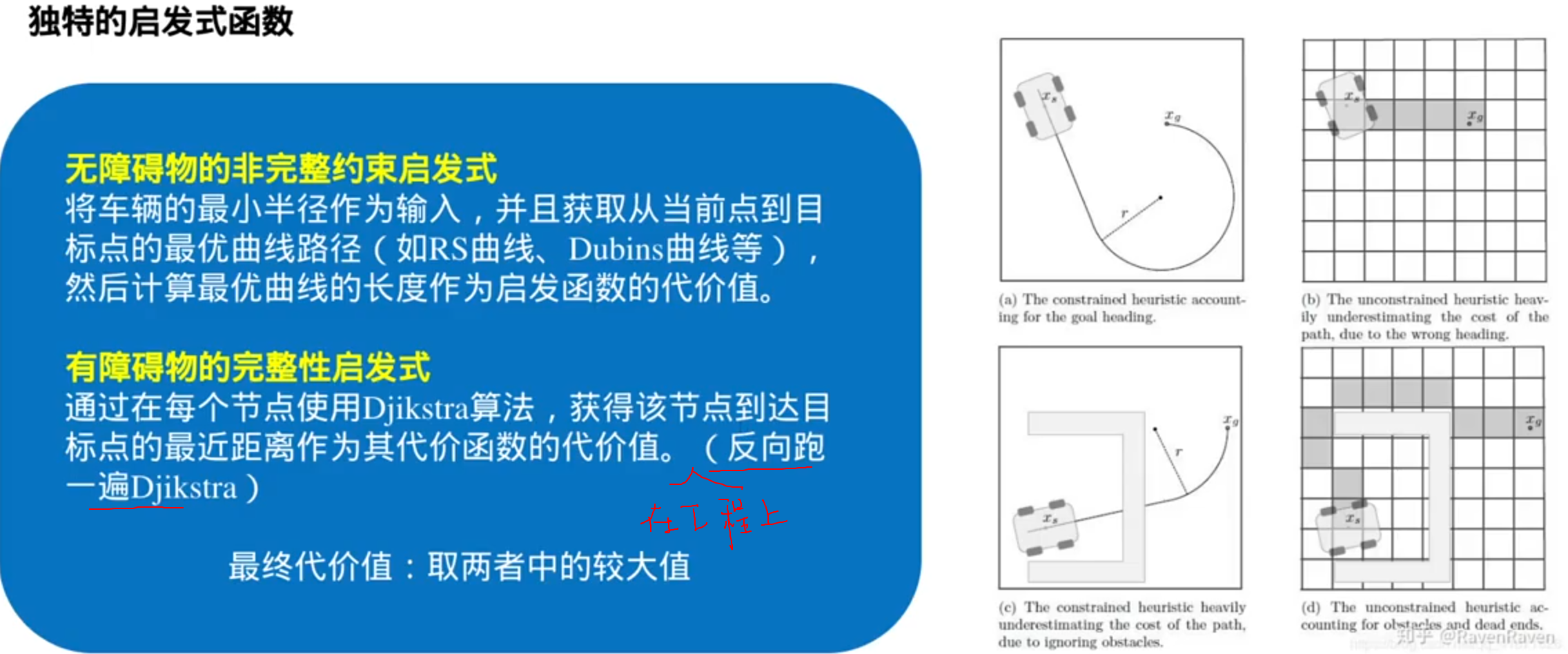
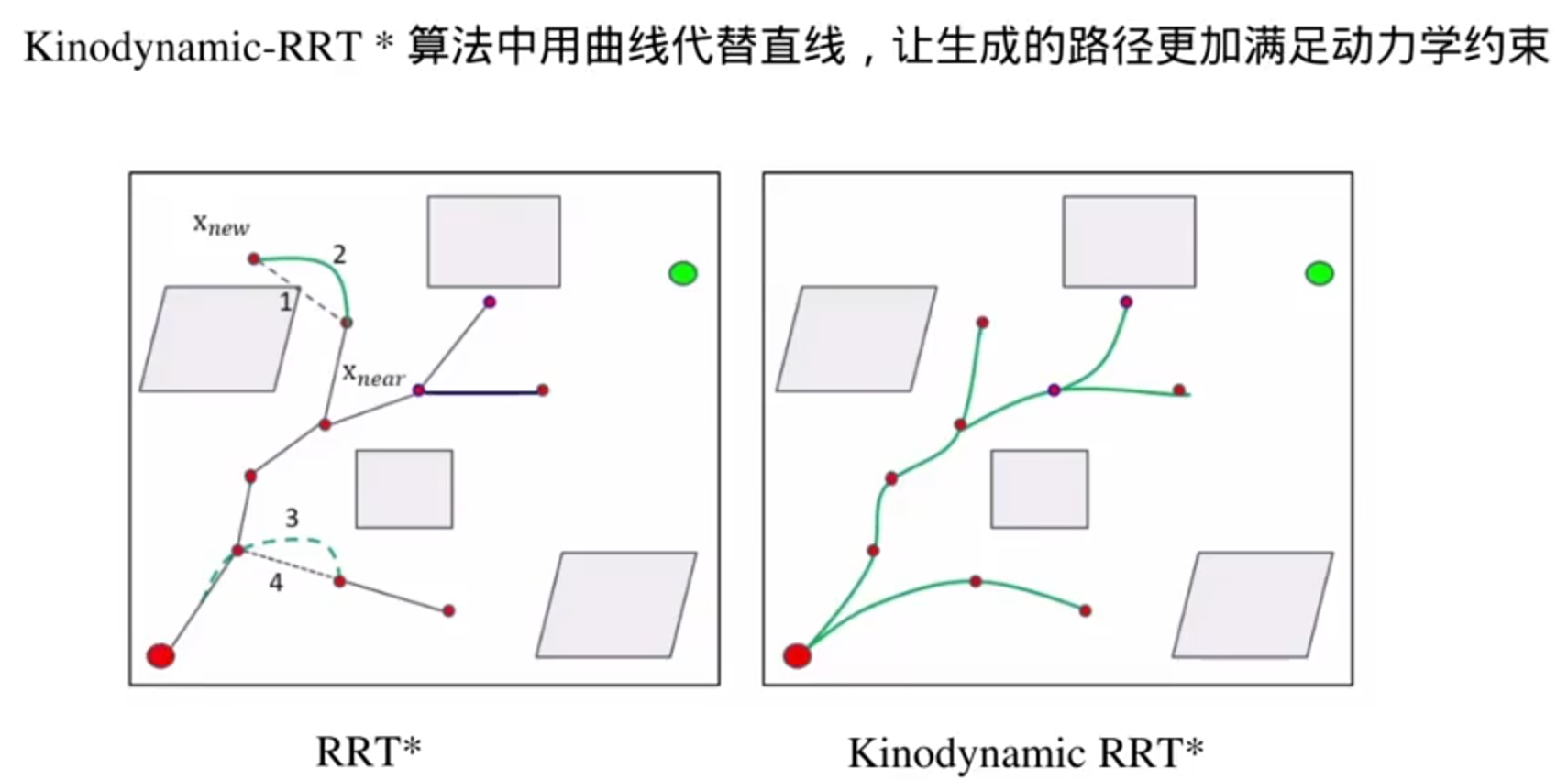
搜索到的路径还要进行轨迹优化

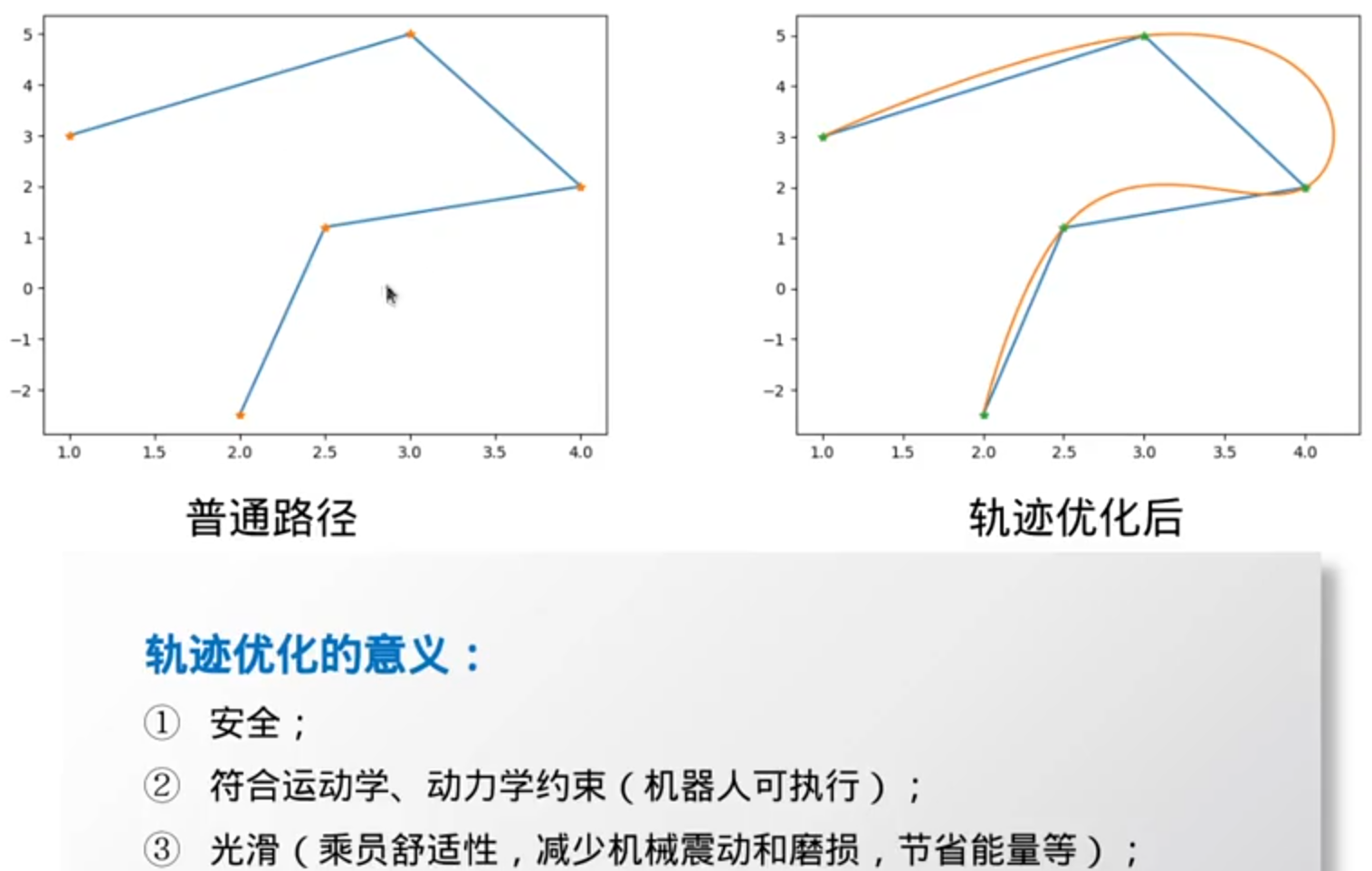
轨迹优化——Min-Jerk(jerk是加加速度)

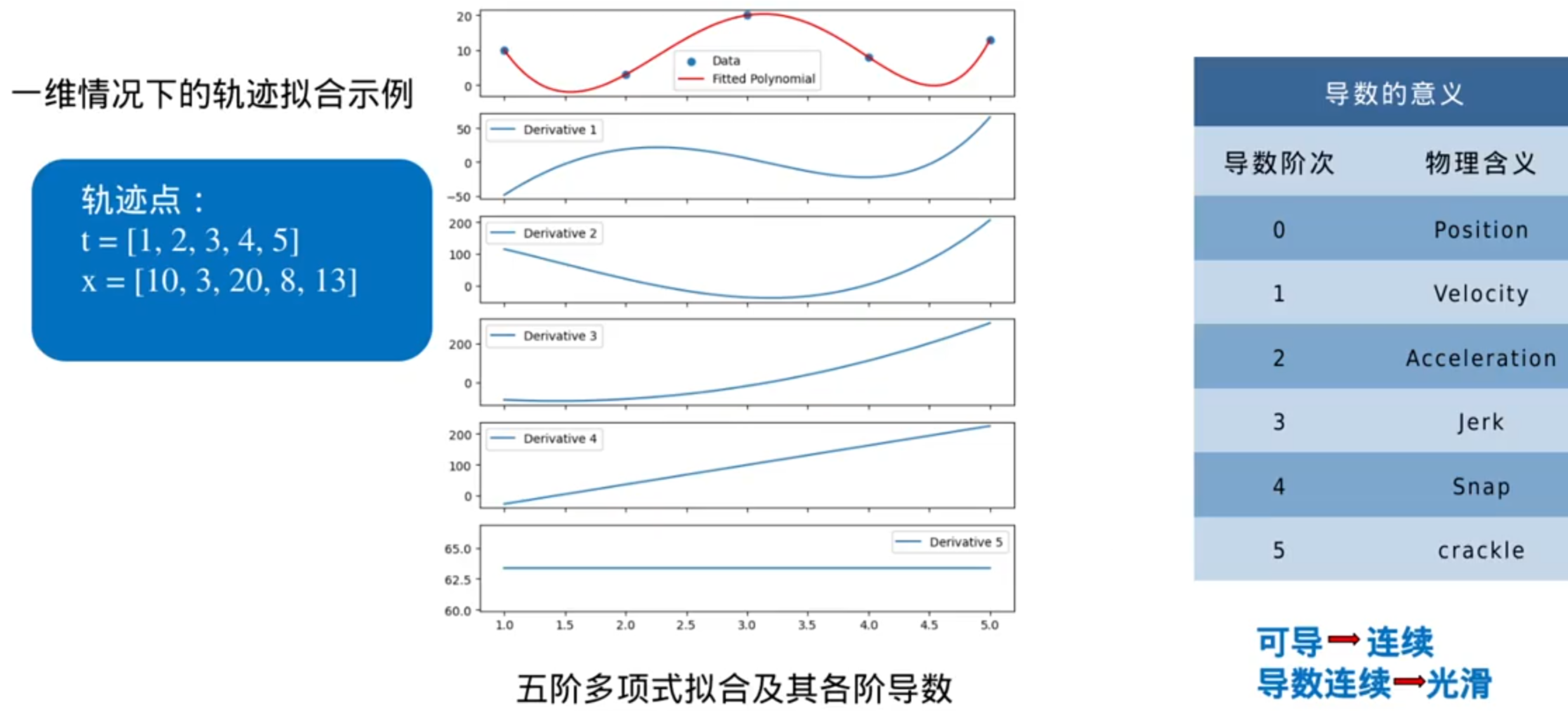
贝塞尔曲线把对连续曲线的规划，转变为对控制点的规划

贝塞尔曲线还有一个巨大的优点：导数还是贝塞尔曲线，仍然有控制点

缺点：贝塞尔曲线的形状完全依赖于控制点的数量和位置

移动一个控制点可能会对曲线的整体形状产生意想不到的影响，这使得局部控制变得困难

B样条曲线解决这两个问题

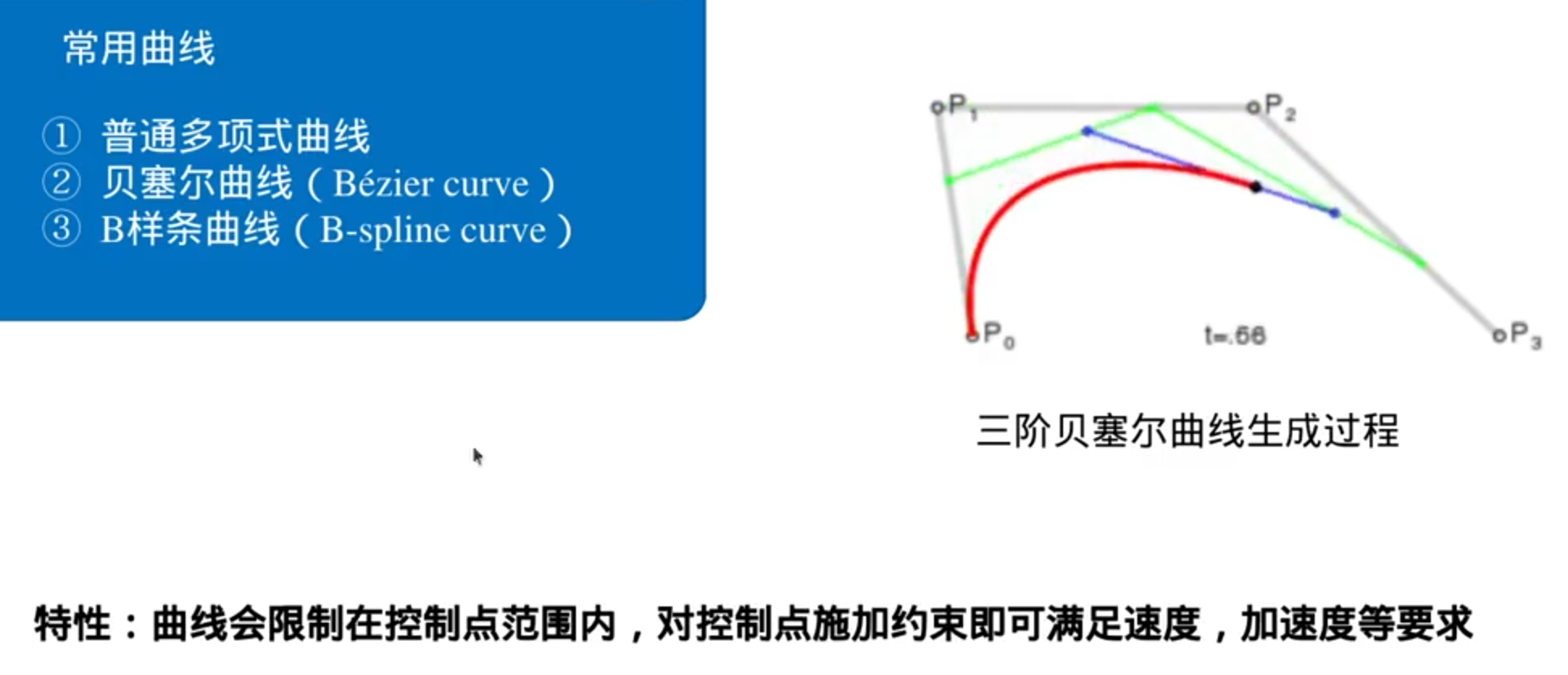
2.

Min-Jerk是舒适性，Min-Snap是节省燃料

lattice planner

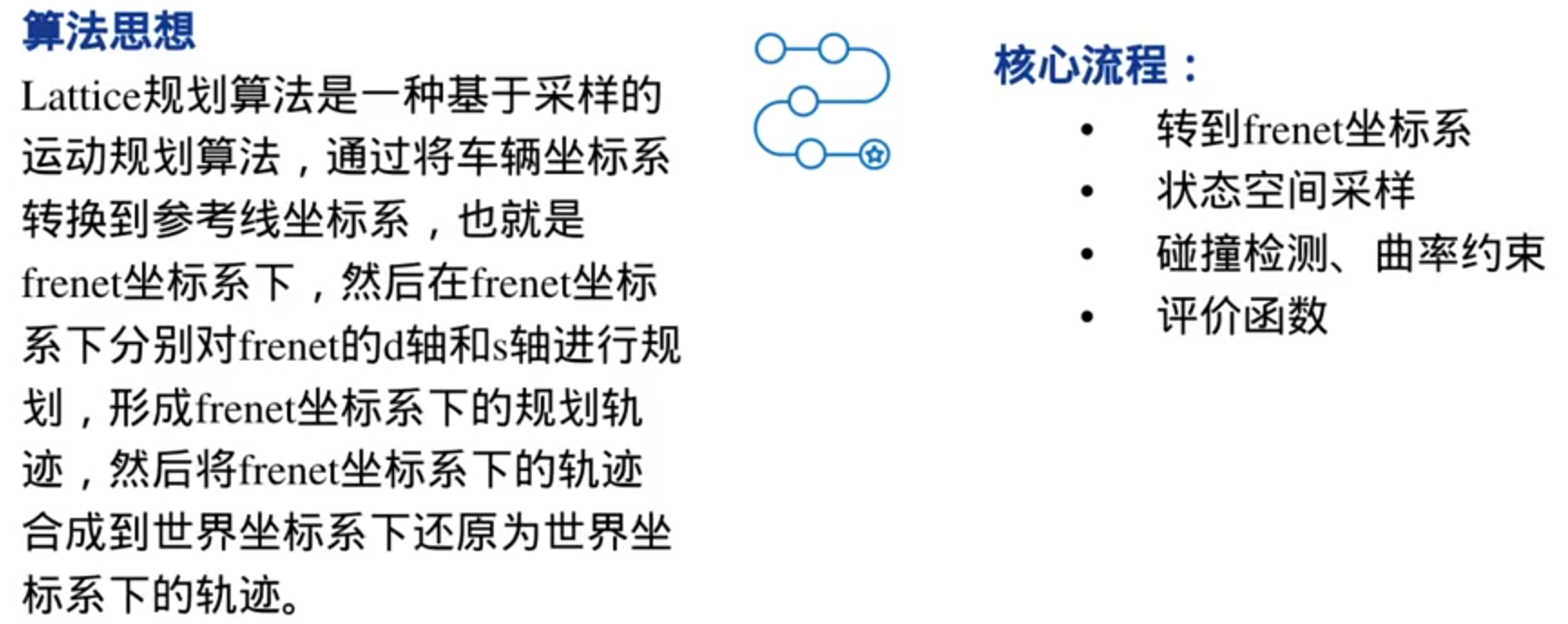
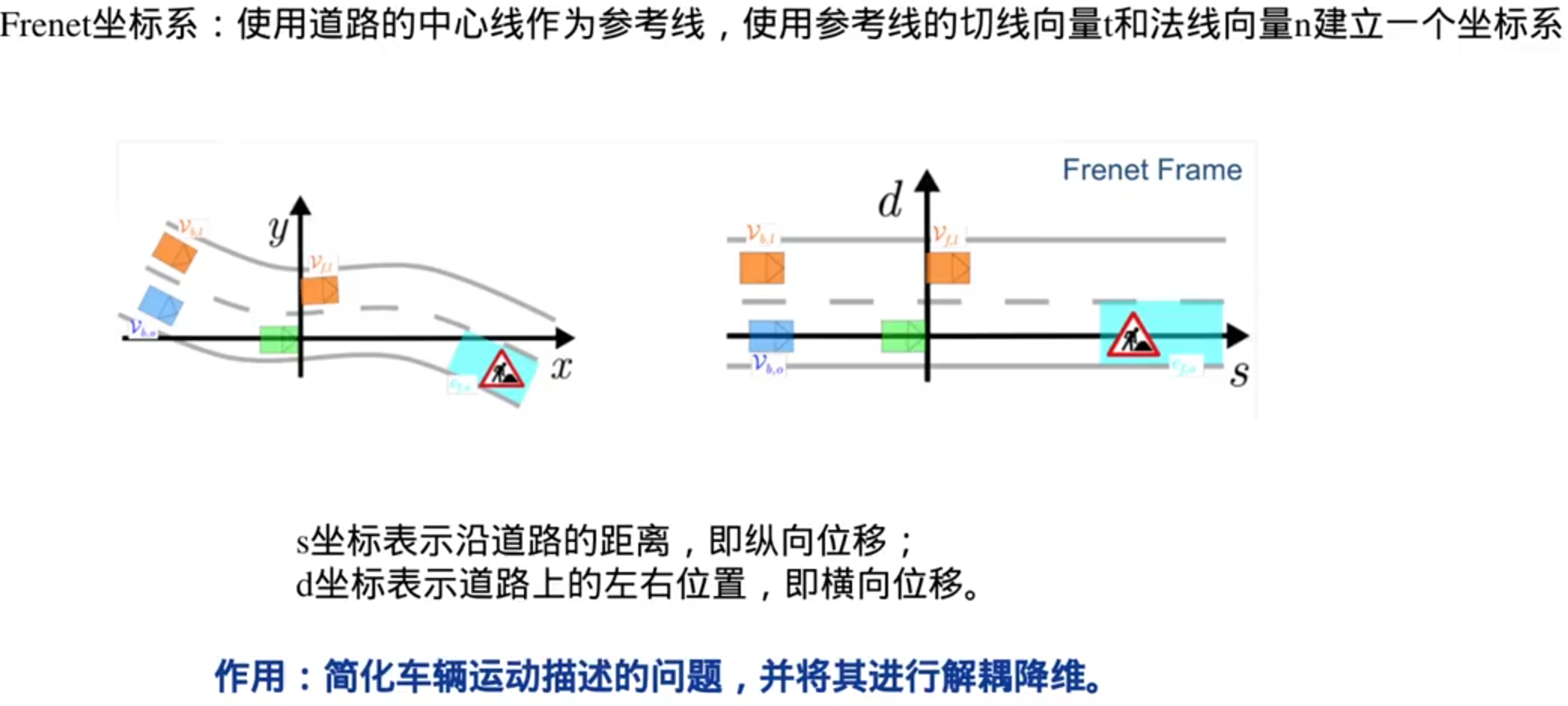
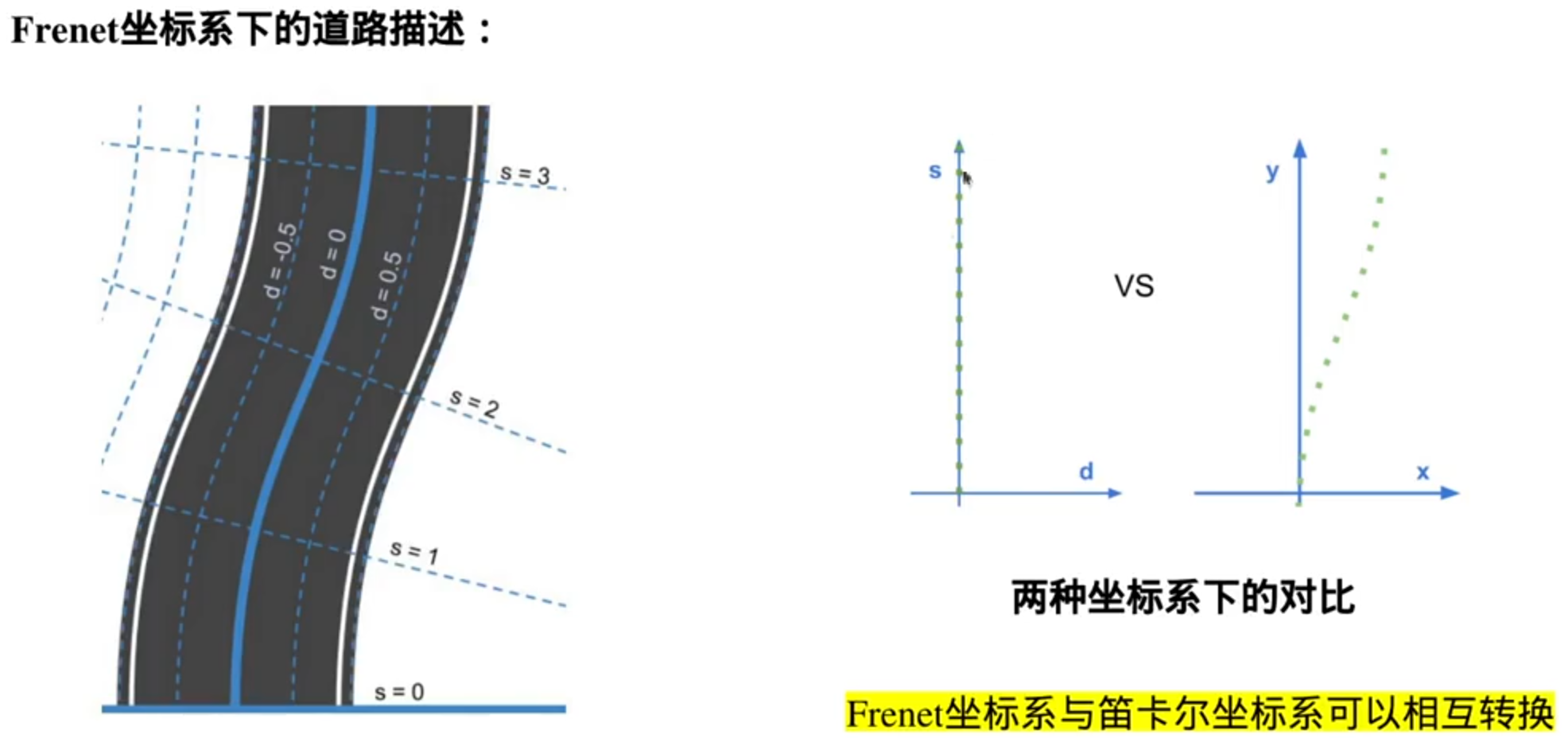
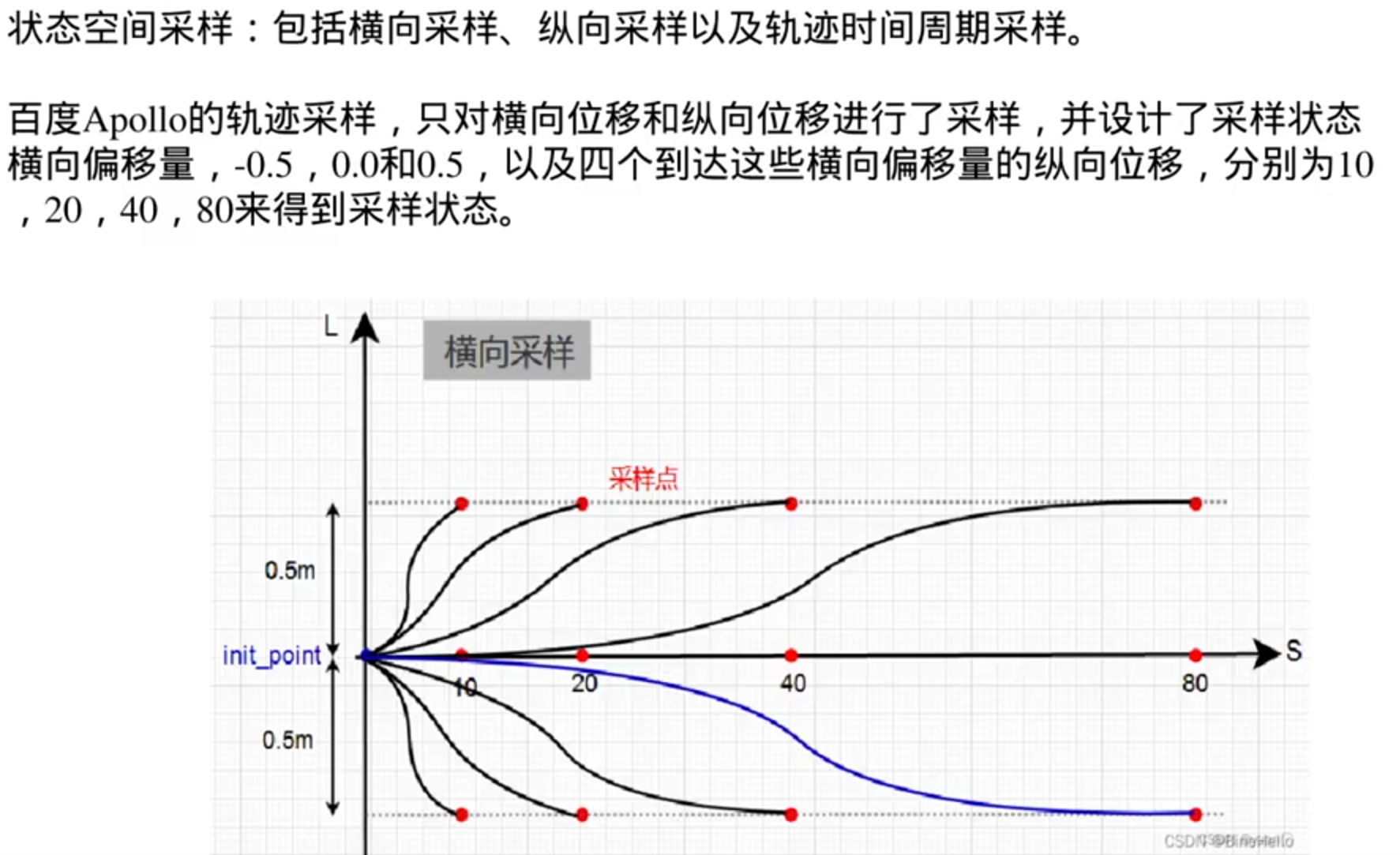
轨迹跟踪

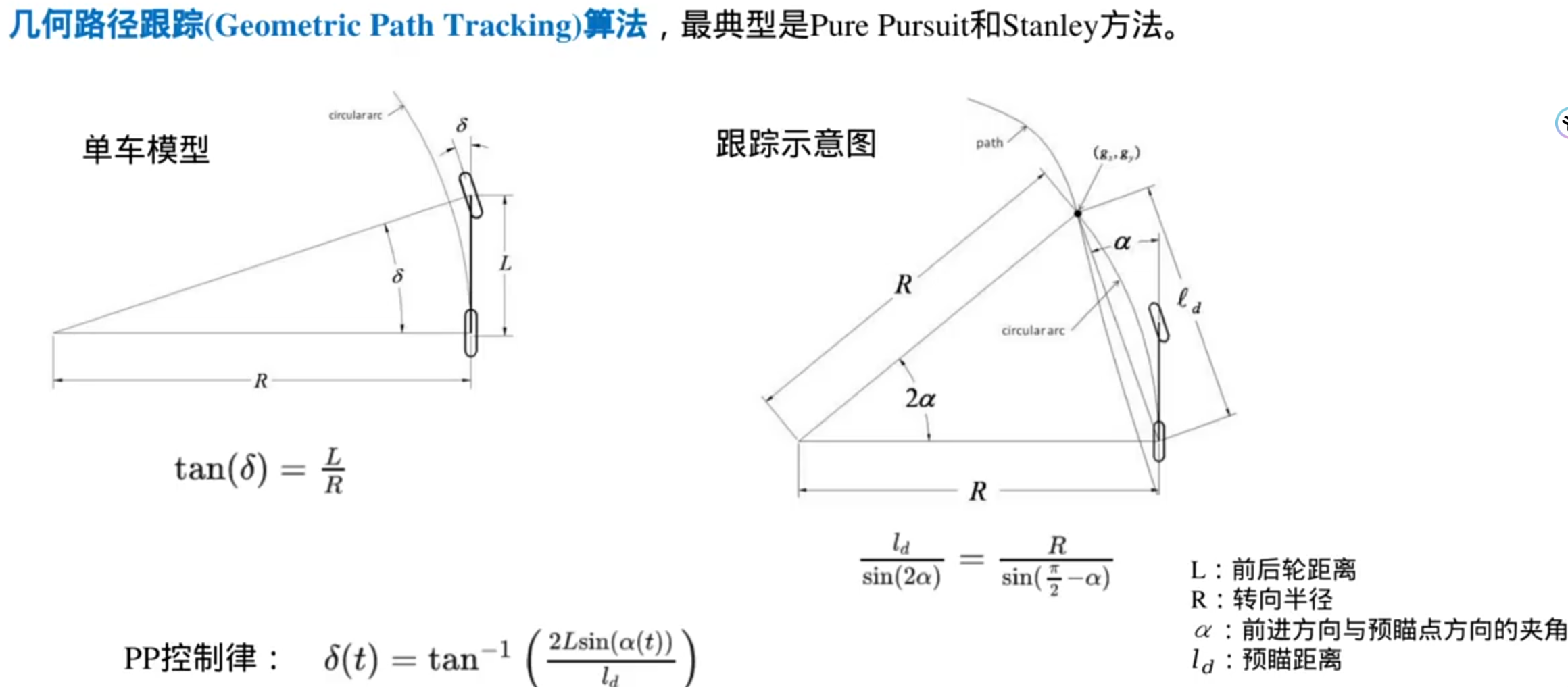
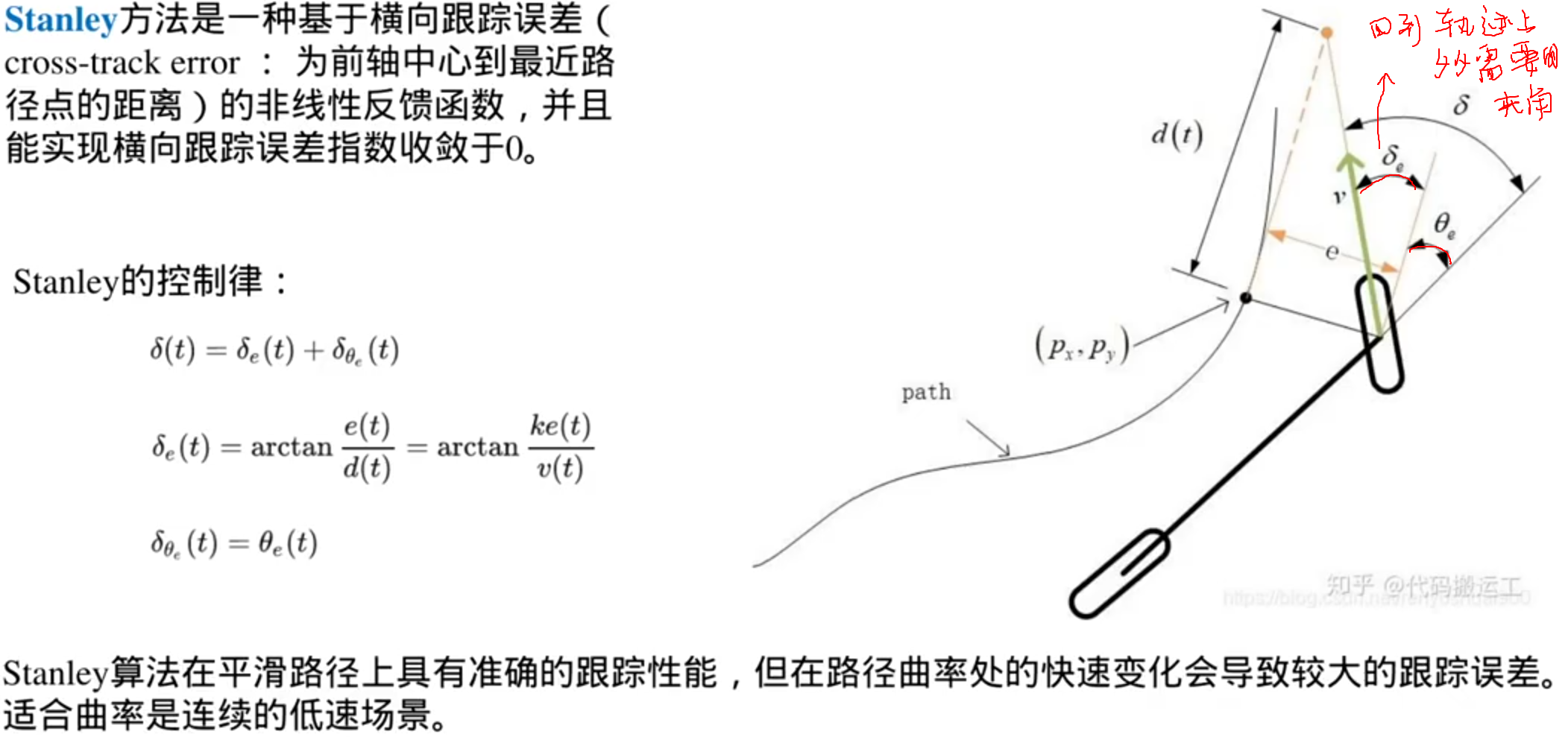
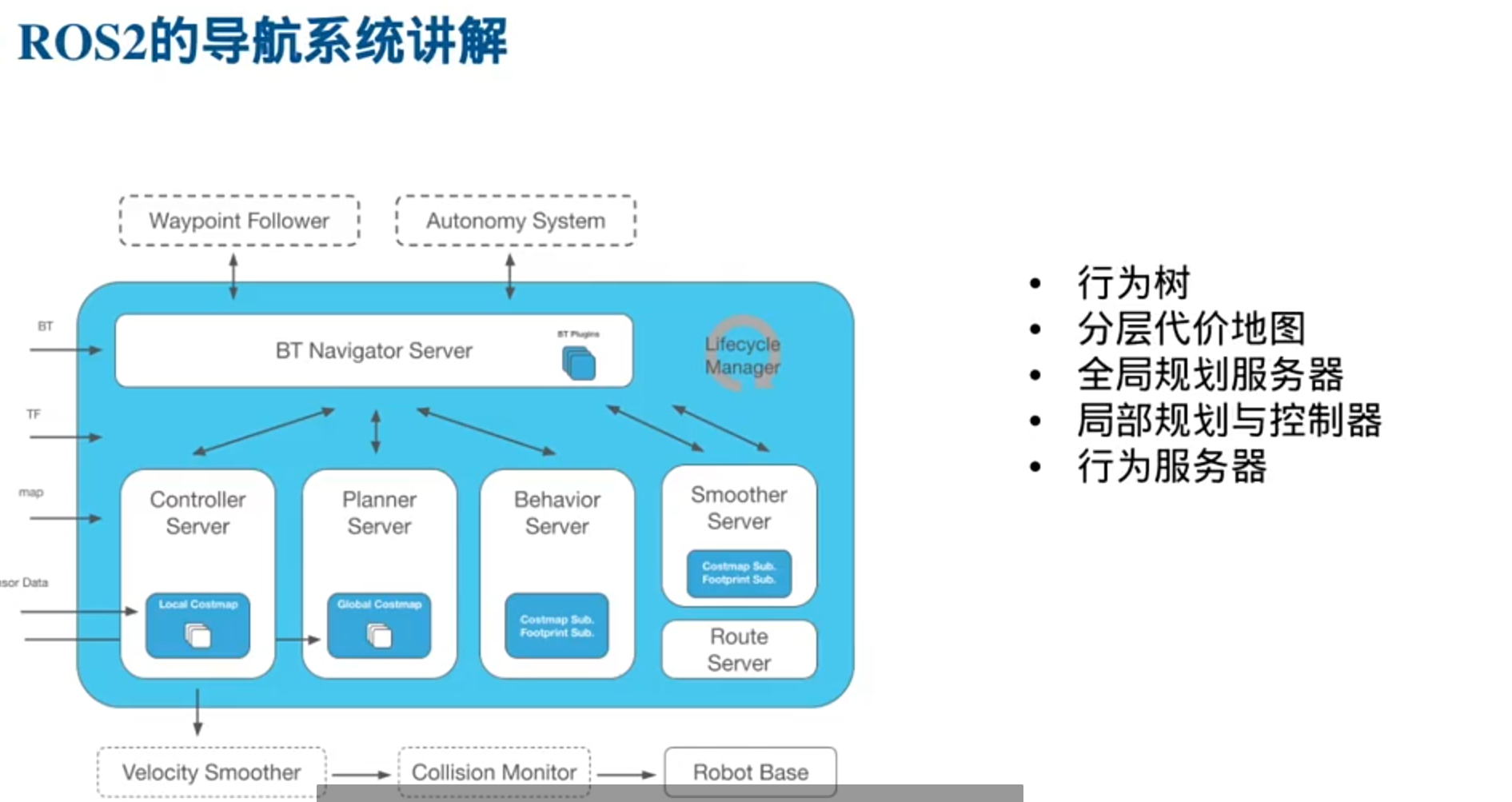
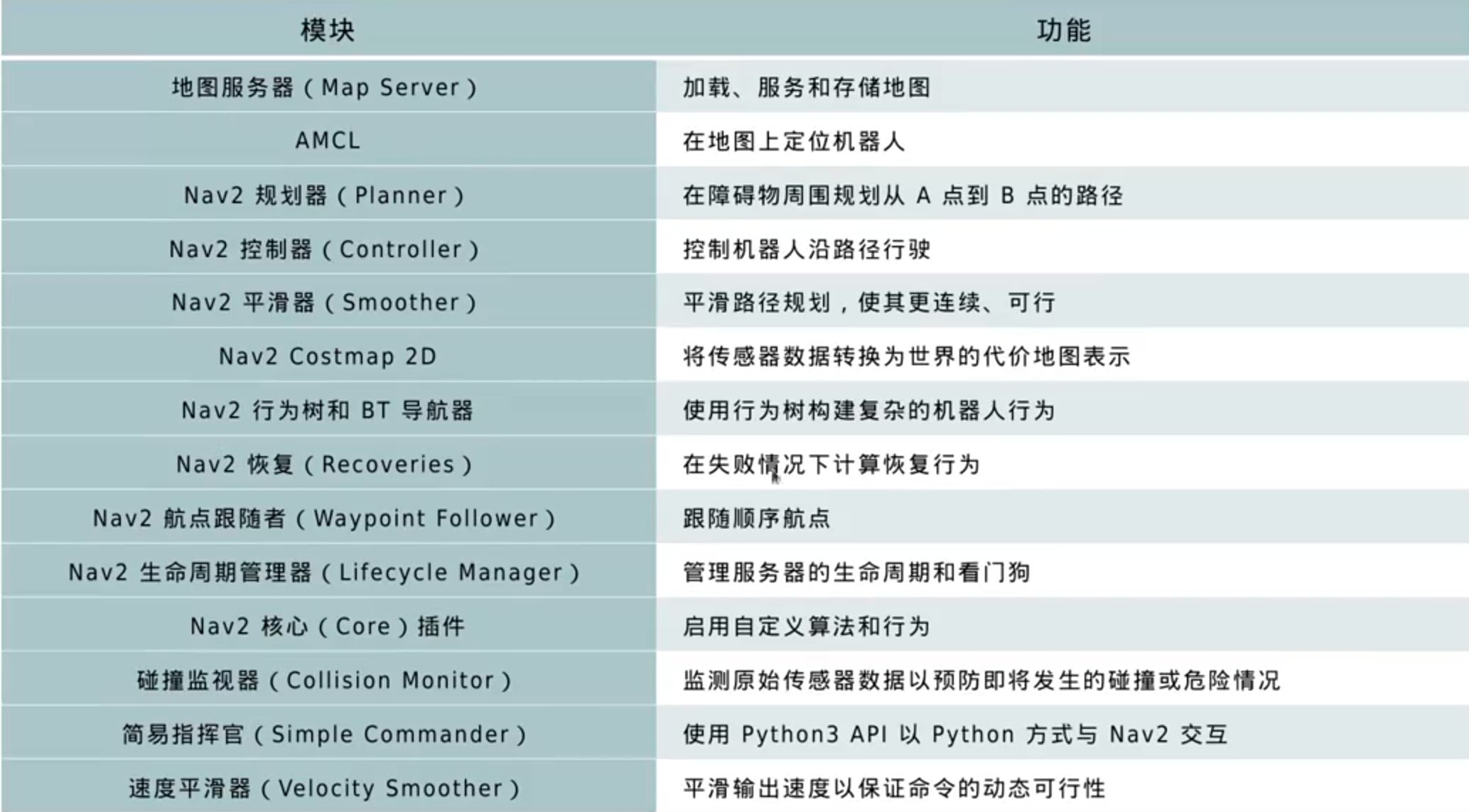
Navigation2组成模块

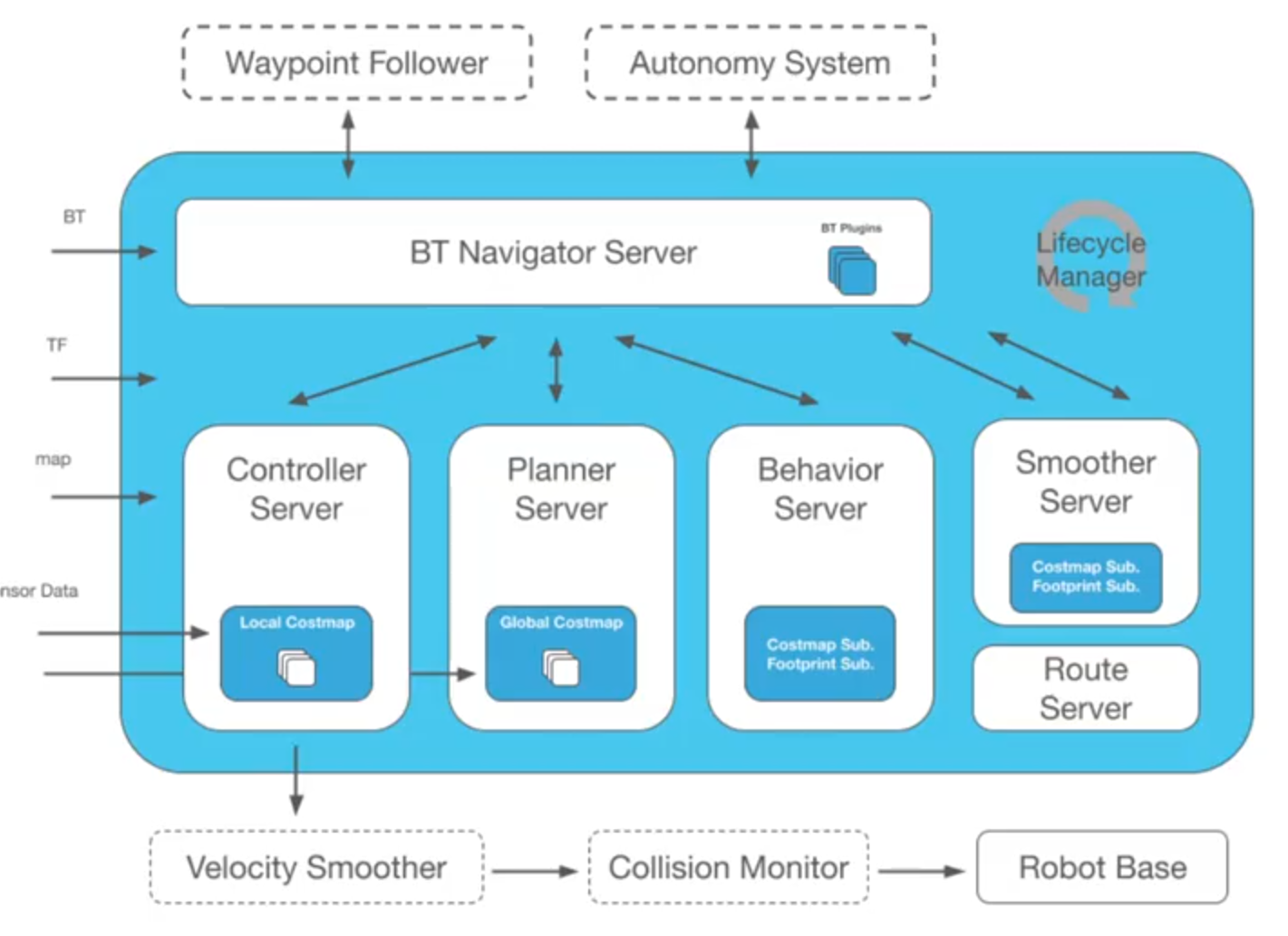
运行流程：

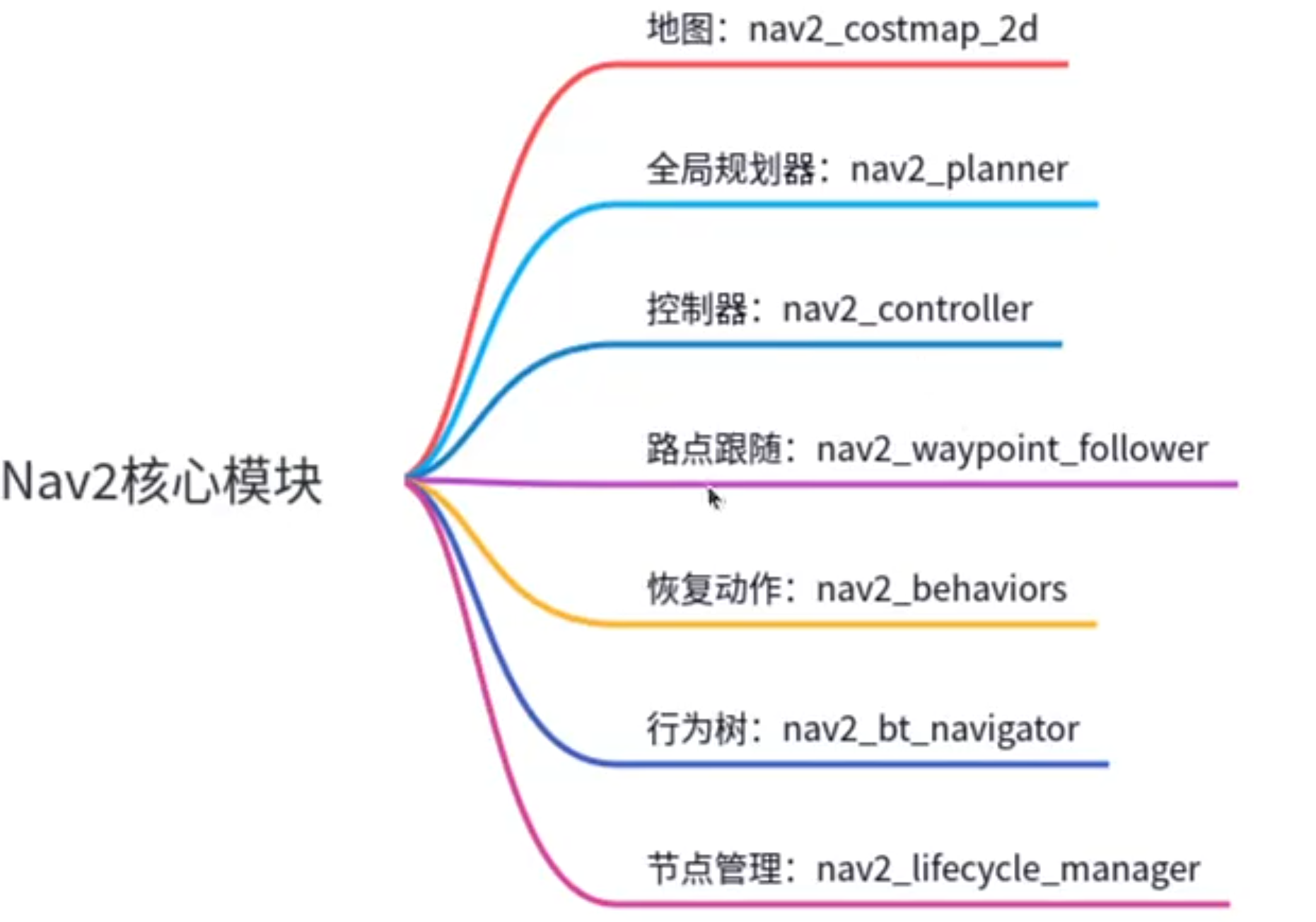
功能包：

Nav2中的地图

代价地图

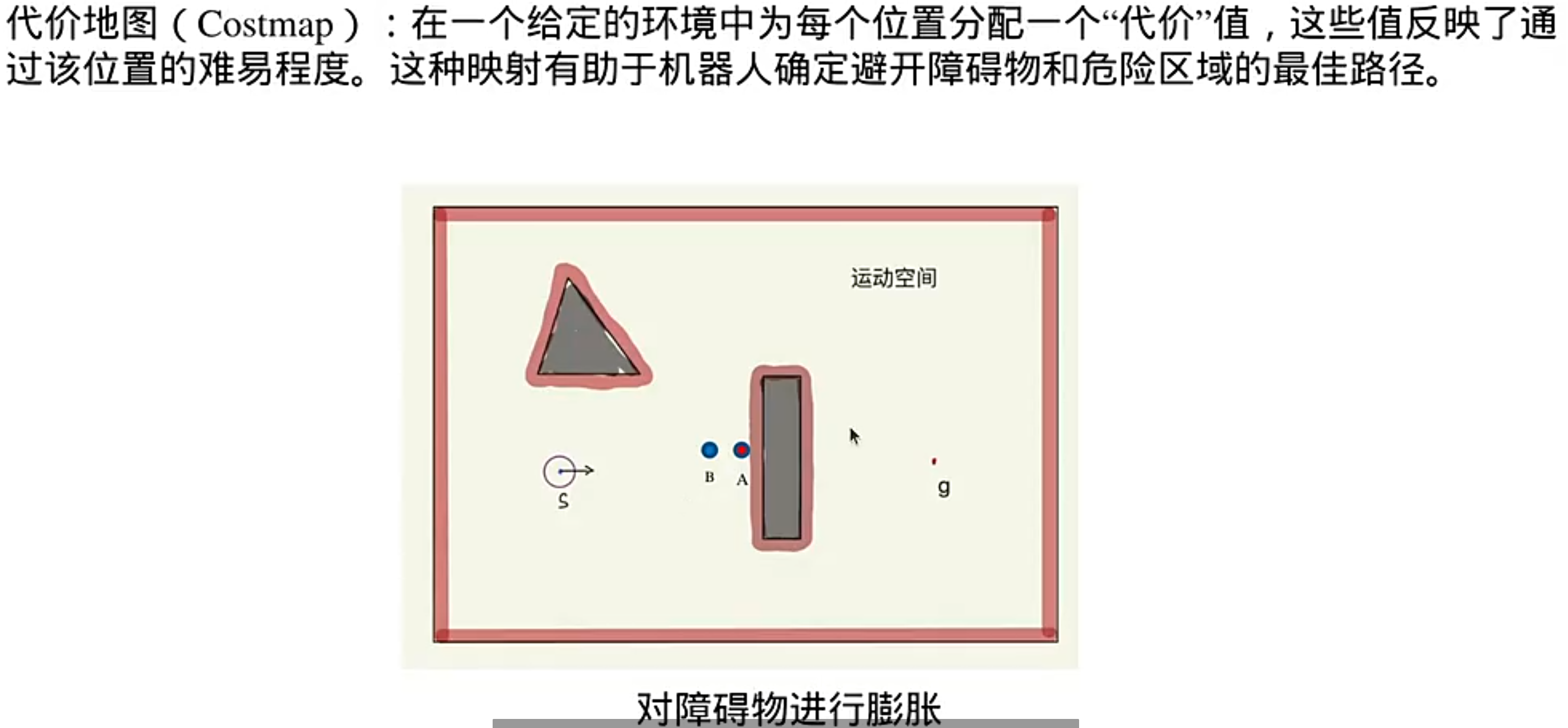
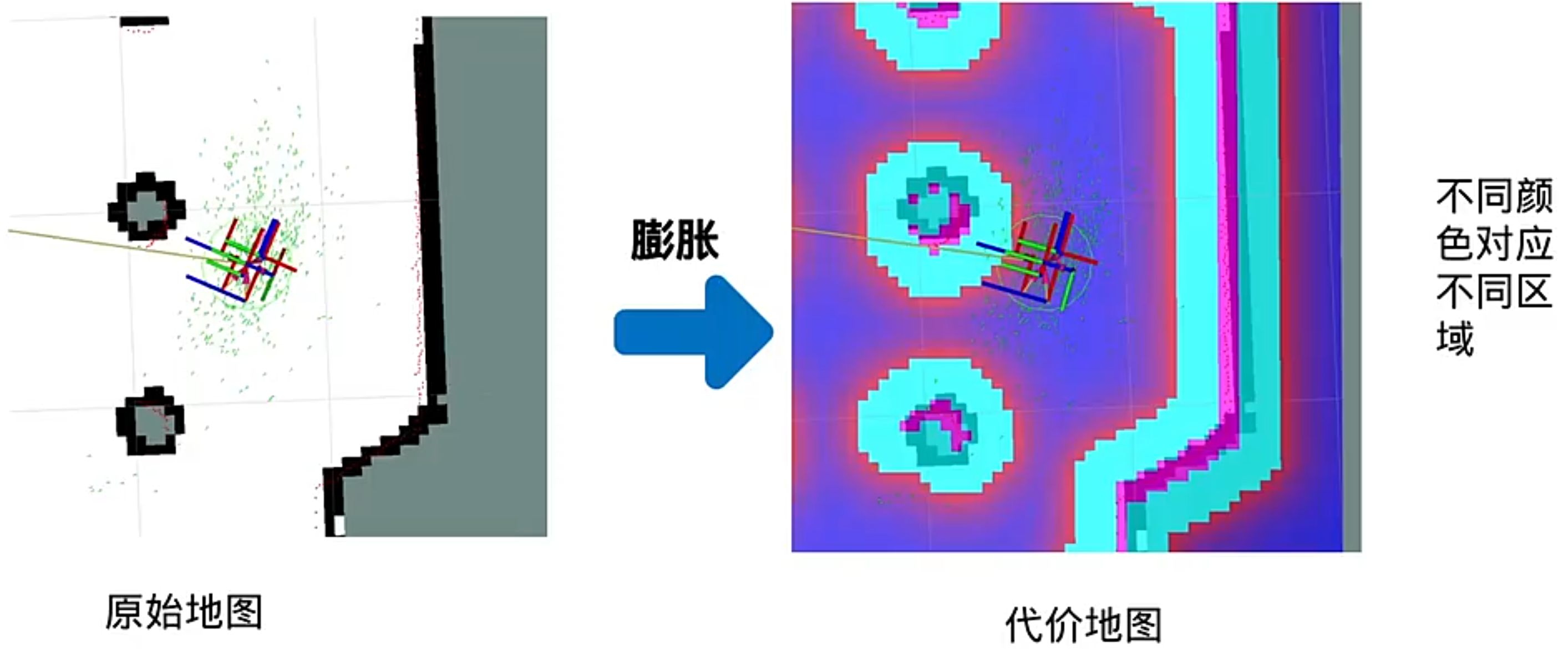
分层代价地图：(直更新有变化的区域)

论文里的分层：

Nav2分层：

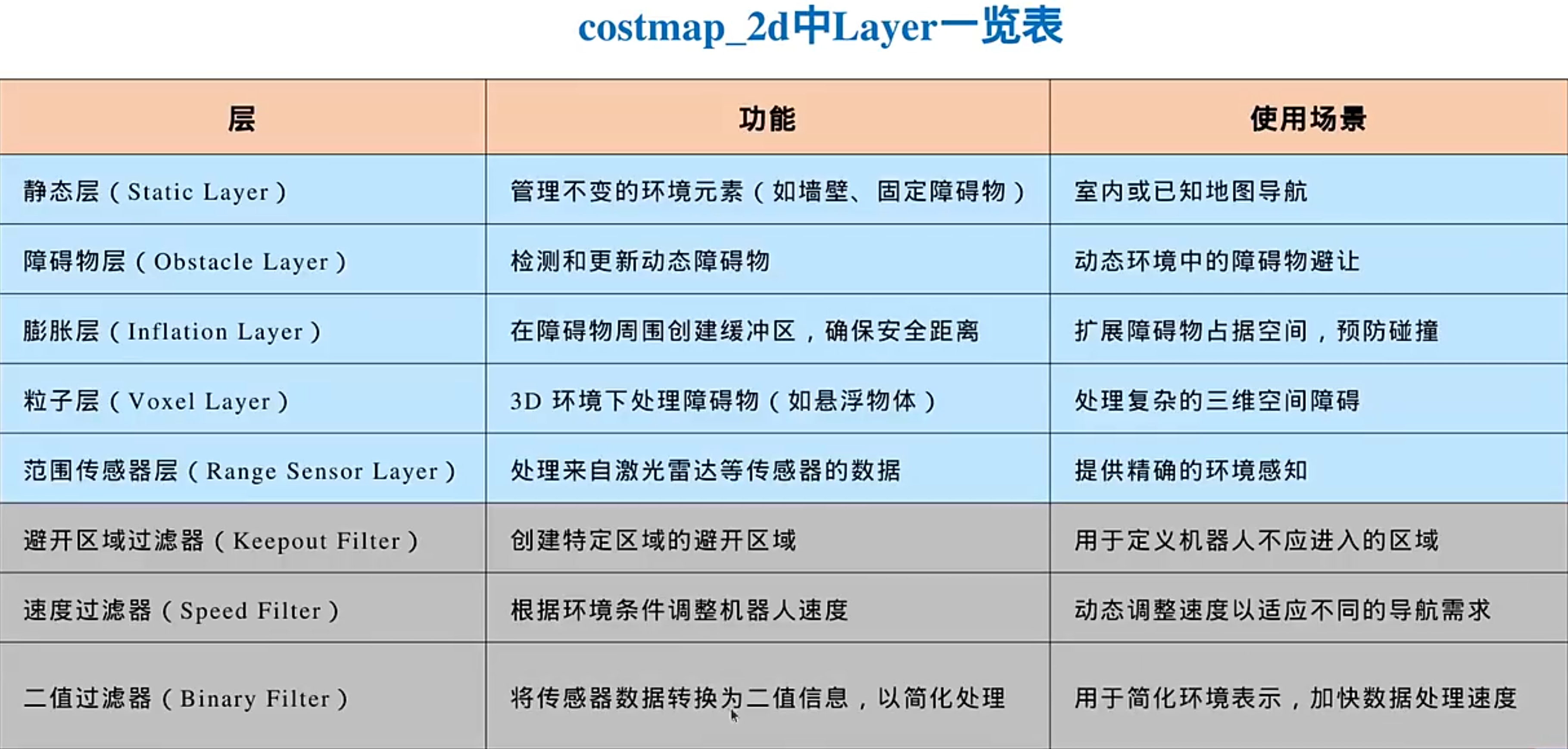
（速度过滤器：限速区）

重启蓝牙服务：

sudo systemctl restart bluetooth

代价地图局部更新的过程：

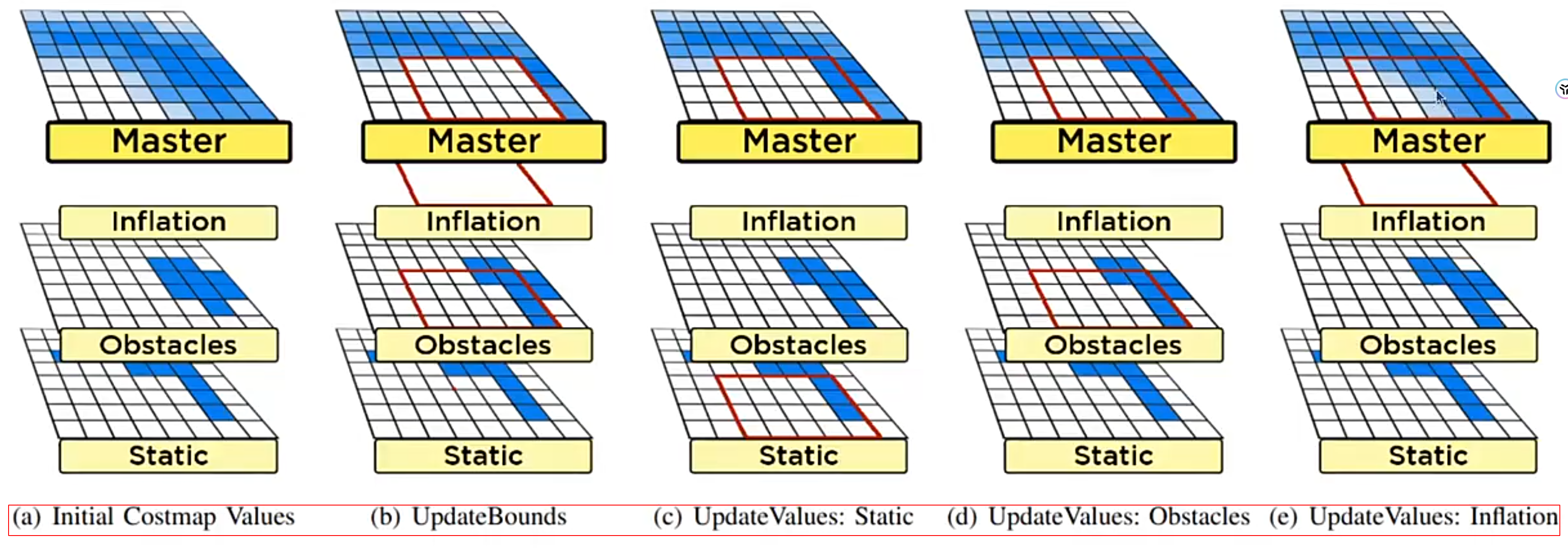
更新边界，更新值

Nav2的核心特点是使用插件机制，插件机制的实现过程是每个层去继承一个基类

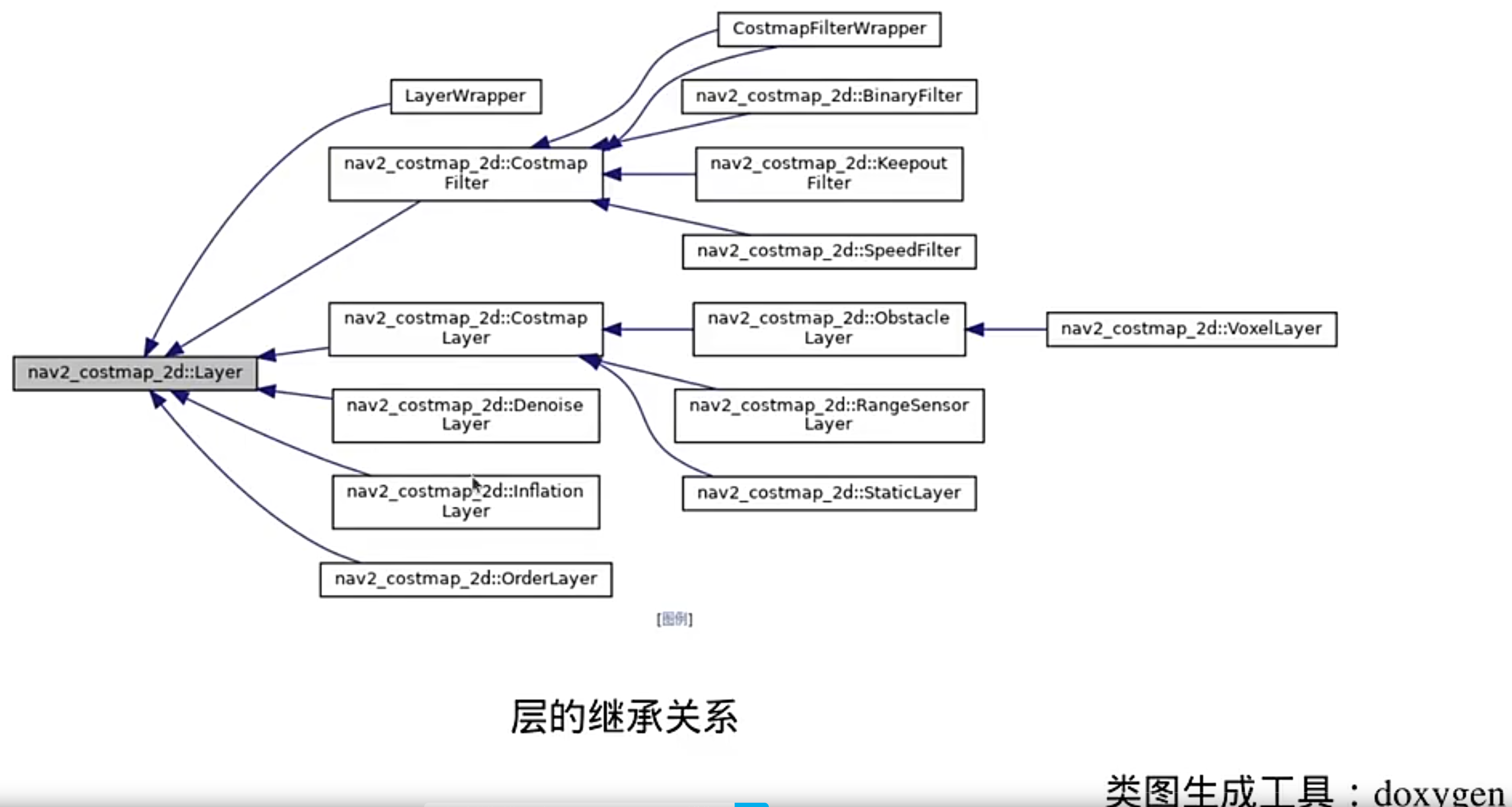
膨胀层具体实现：

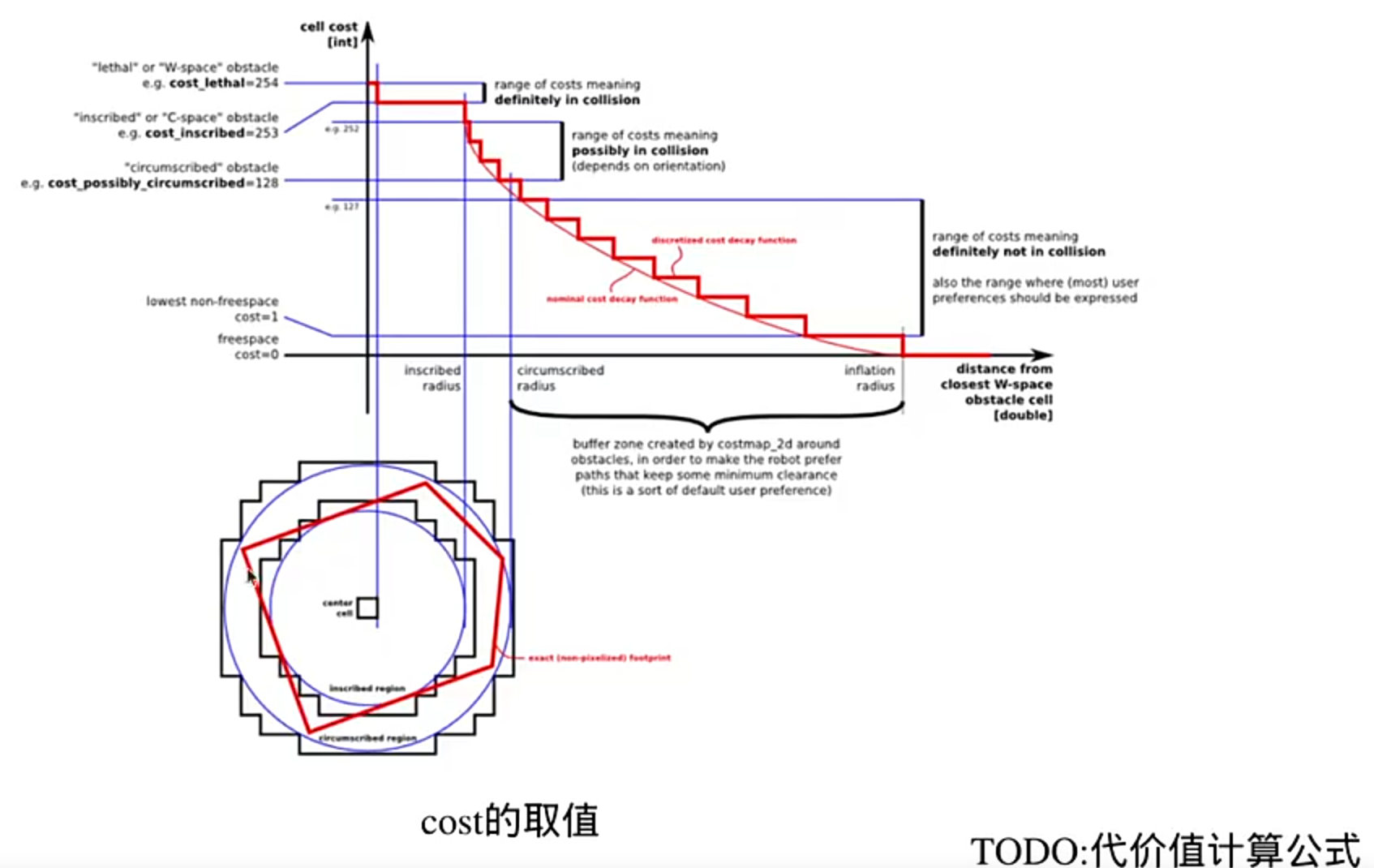
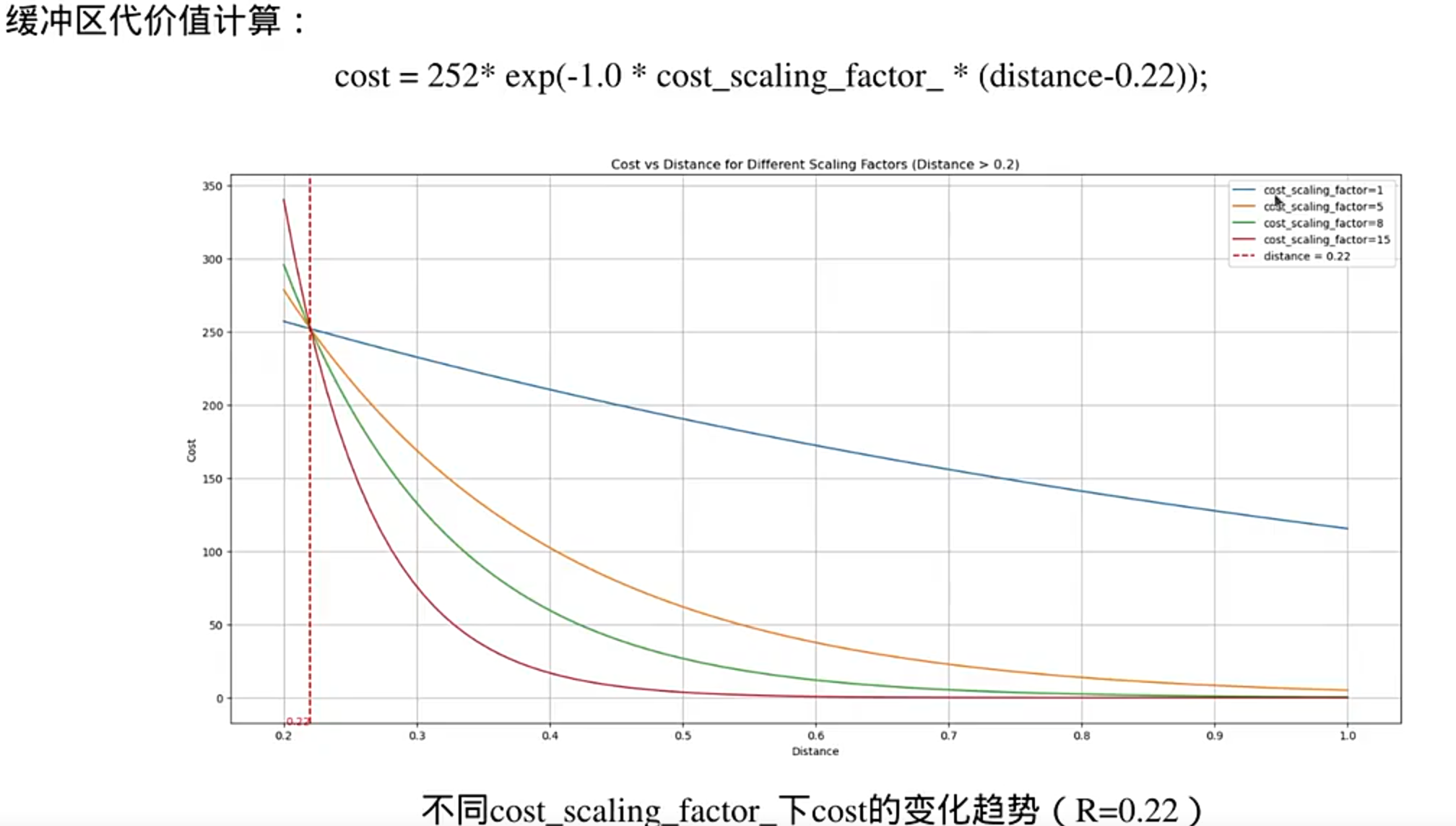
限速区具体实现：

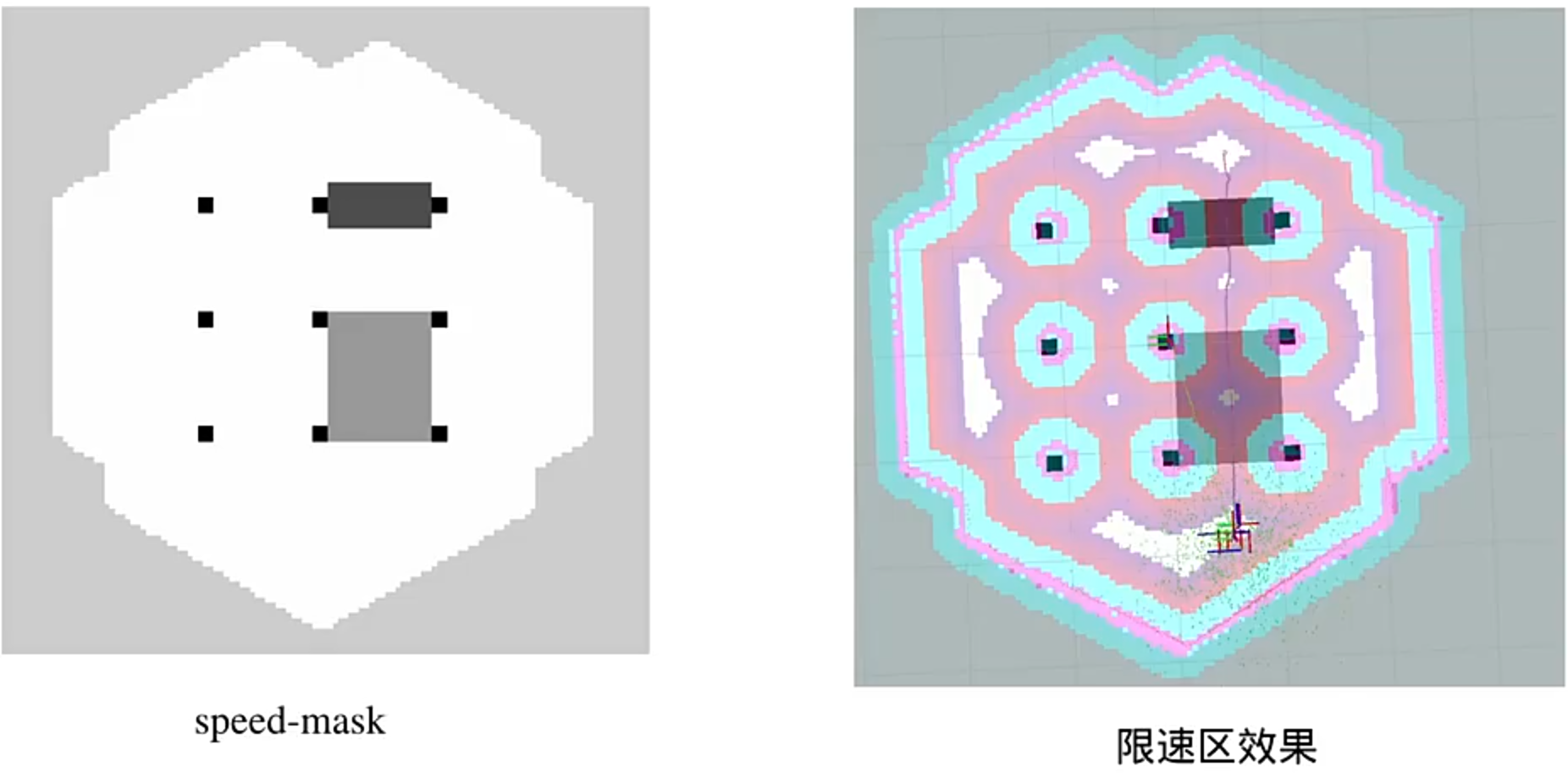
配置参数

机器人坐标系：

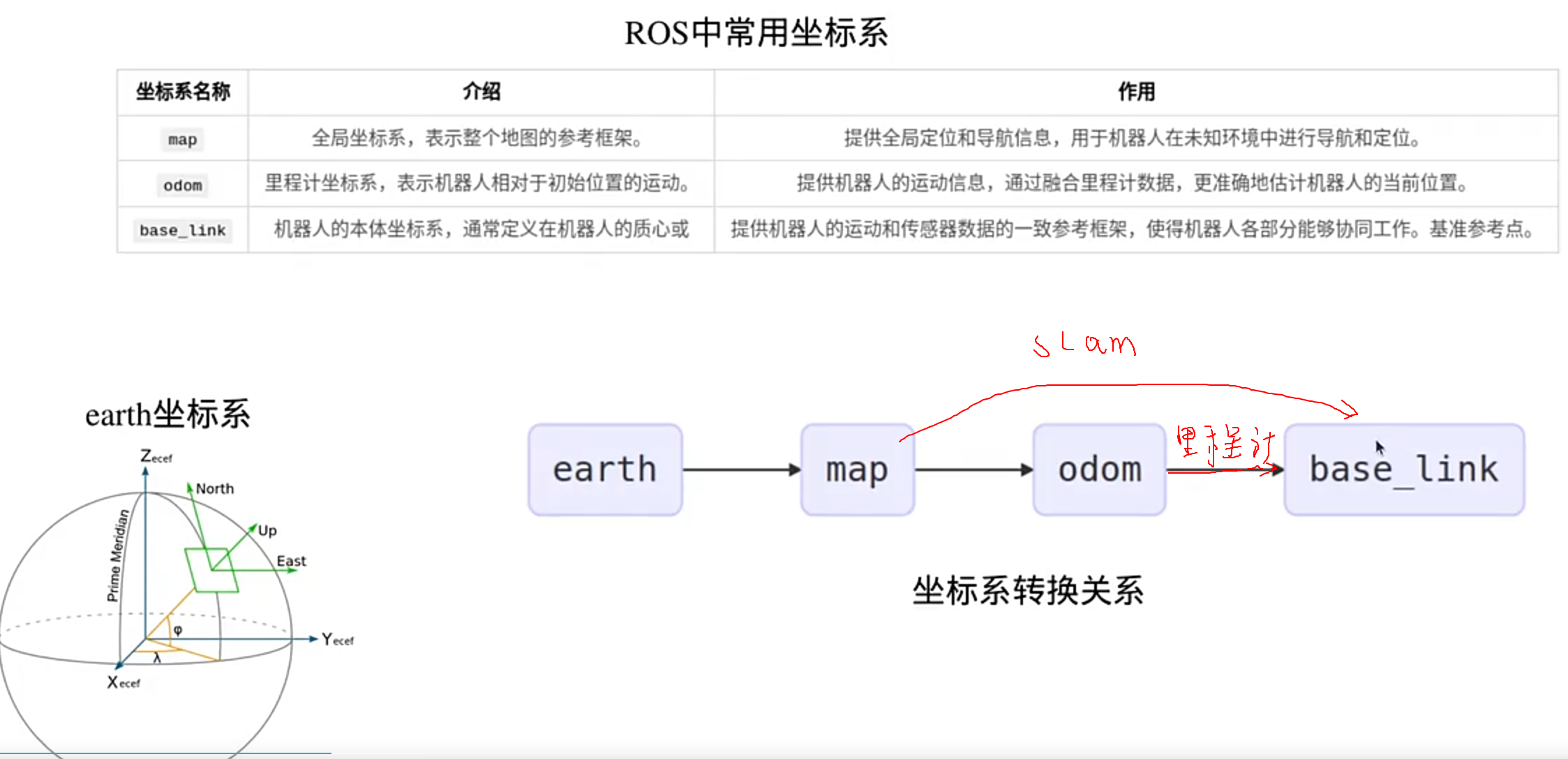
(TF树里只能有一个parent)

代价地图有两张：

全局路径搜索（静态），局部轨迹优化（动态）

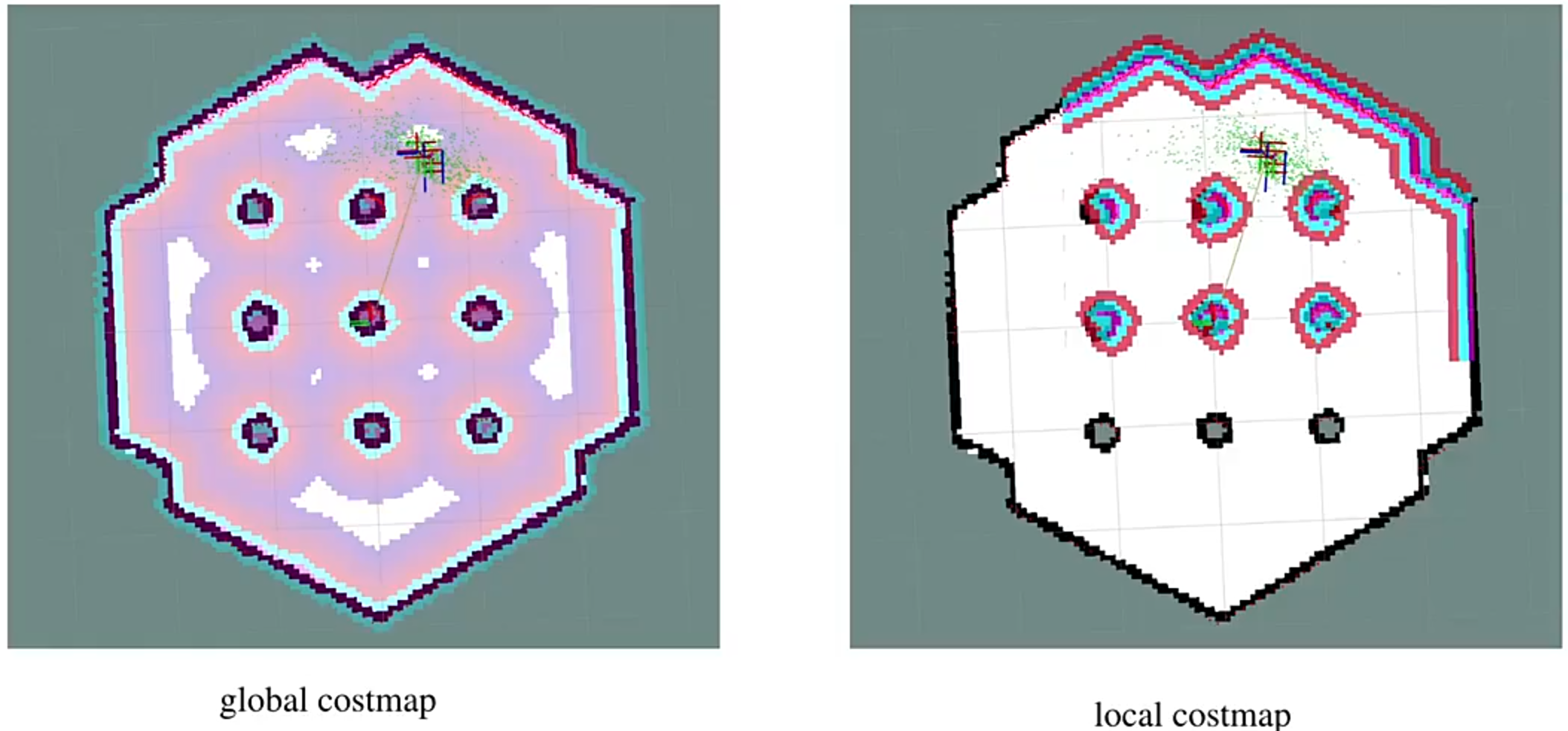
全局代价地图参数：

局部代价地图参数：

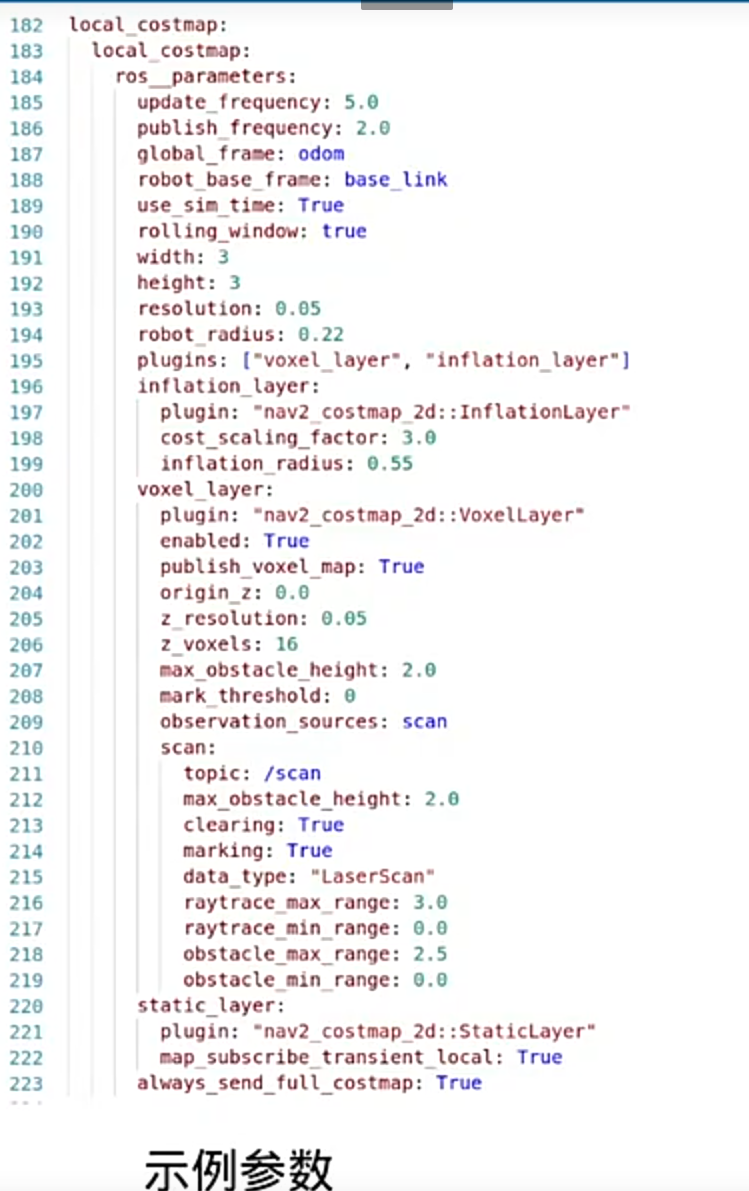
footprint 是机器人在环境中占据的空间的几何形状。这个形状通常用一组坐标点来表示，形成一个多边形。

resolution=0.05 表示地图的分辨率。指每个栅格（grid cell）的大小，以米为单位

全局路径规划服务器

Planner_Server的功能

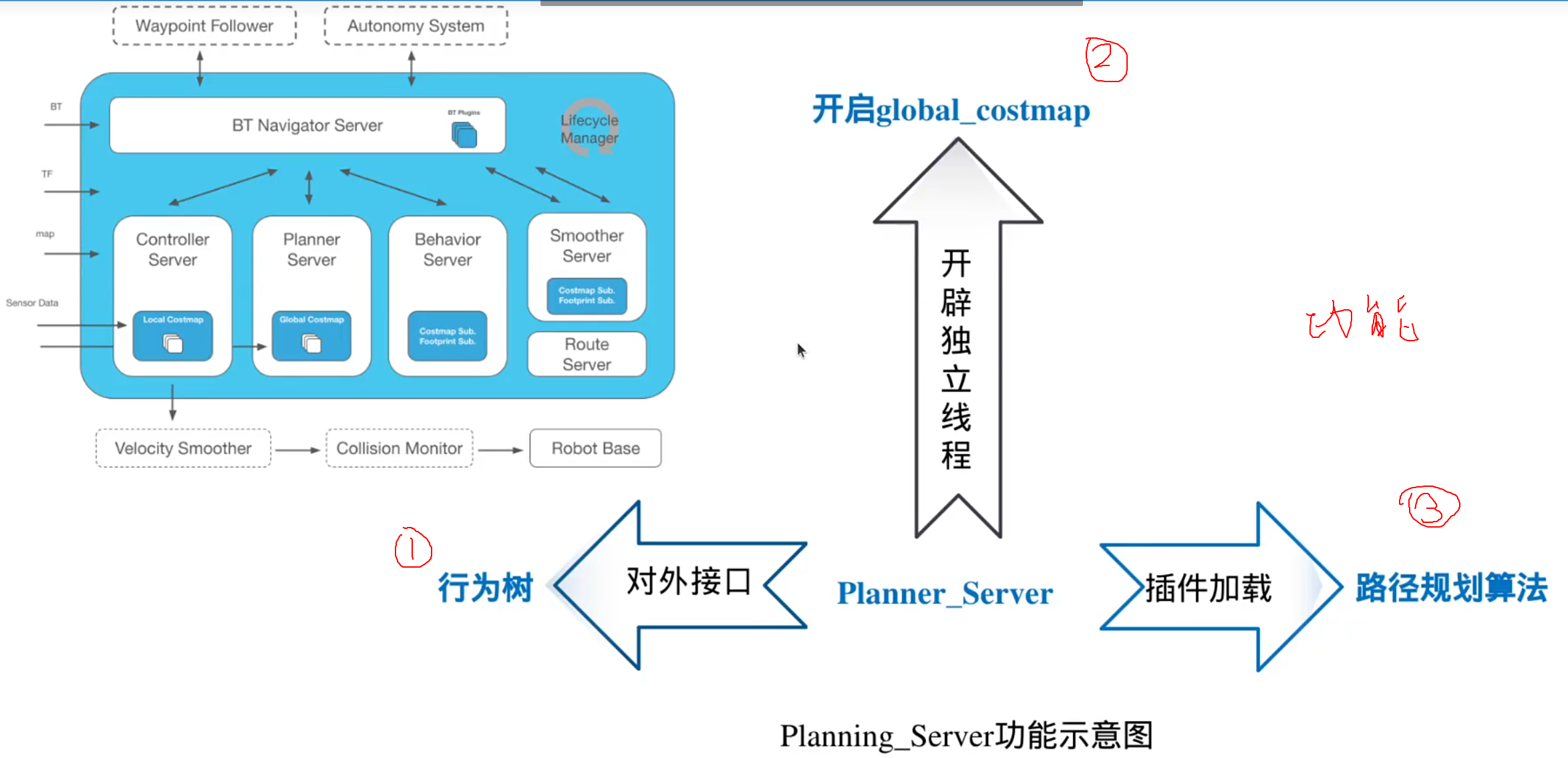
1.对行为树接口：

(navigation2里面使用了大量的action通信机制)

2，开启全局代价地图

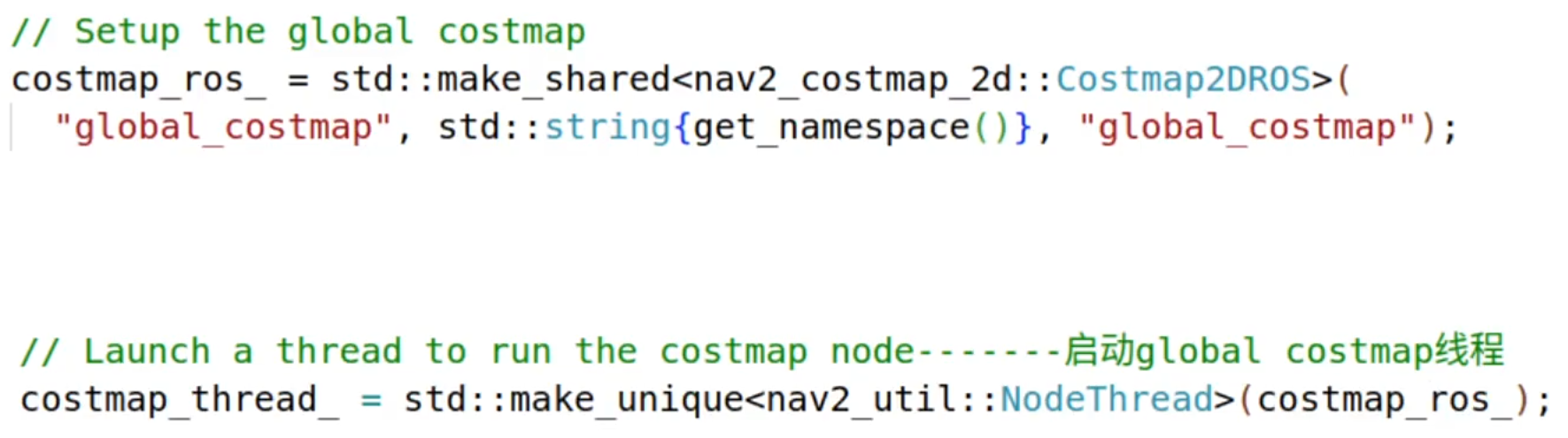
3.加载规划算法

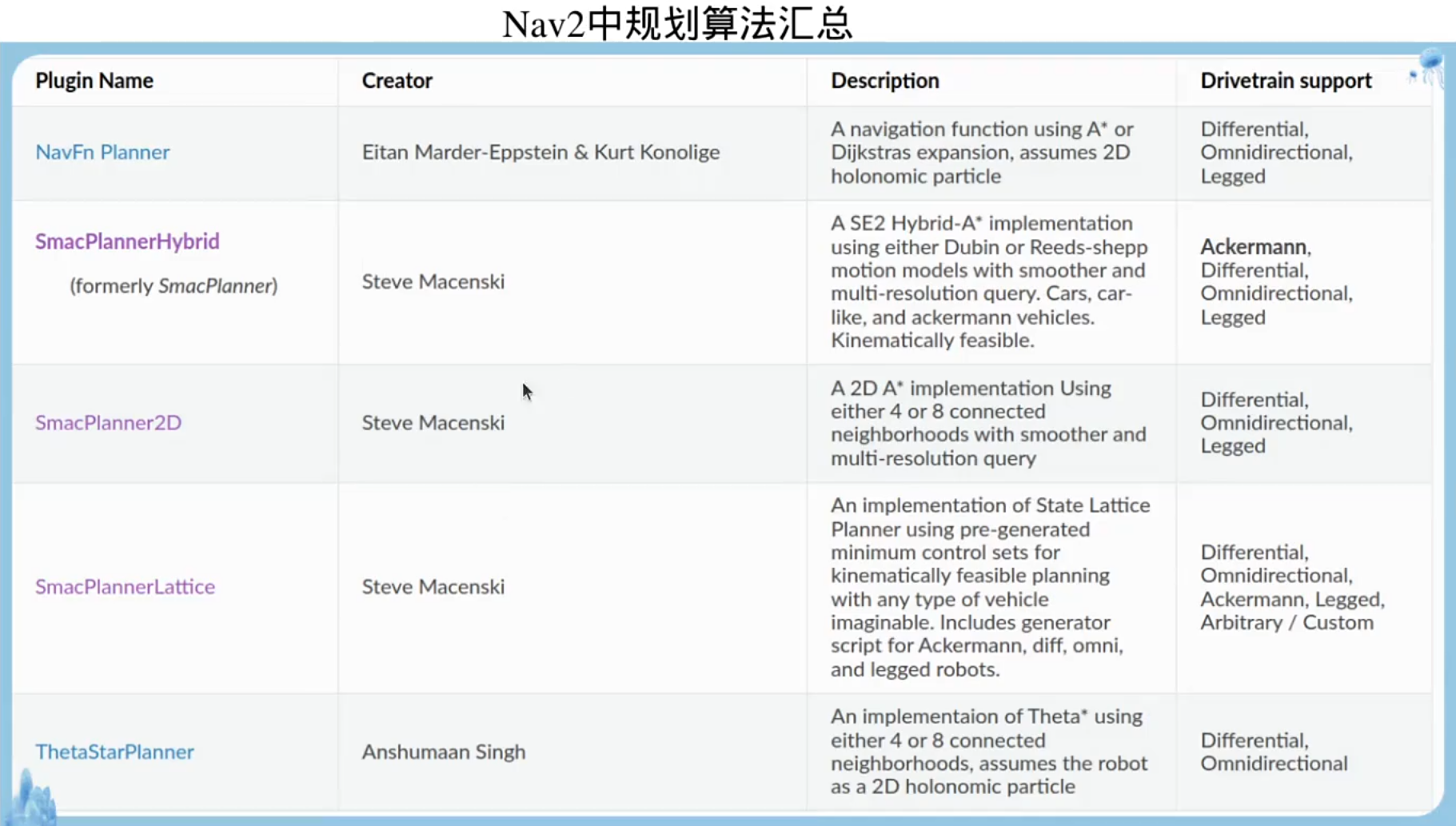
插件机制：

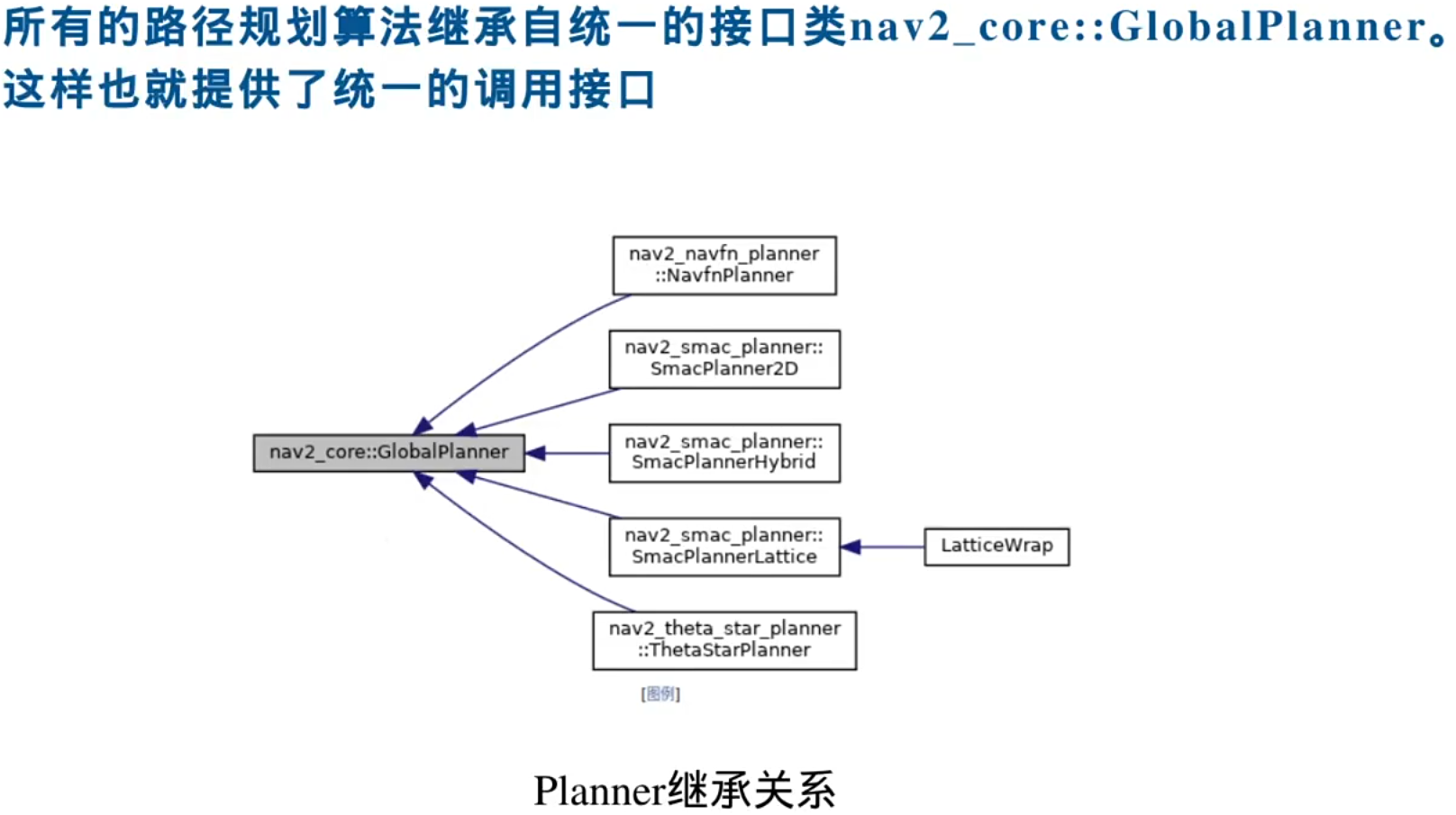
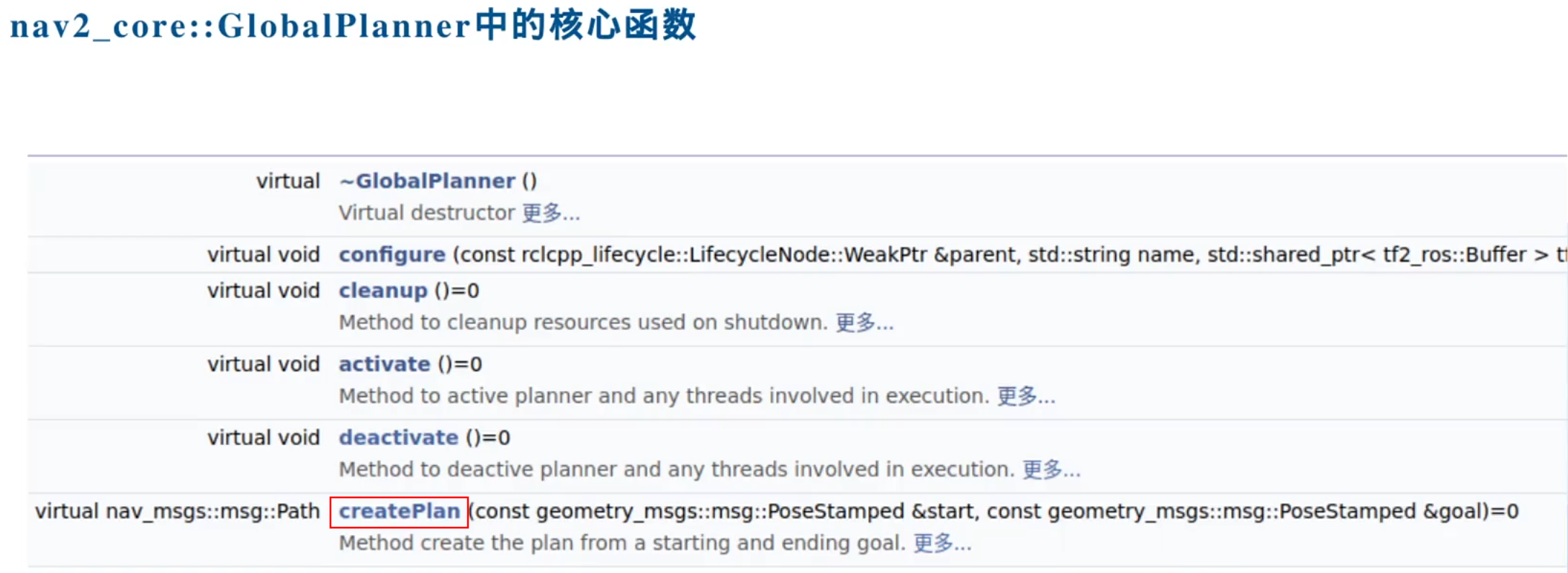
planning_server的源码实现：

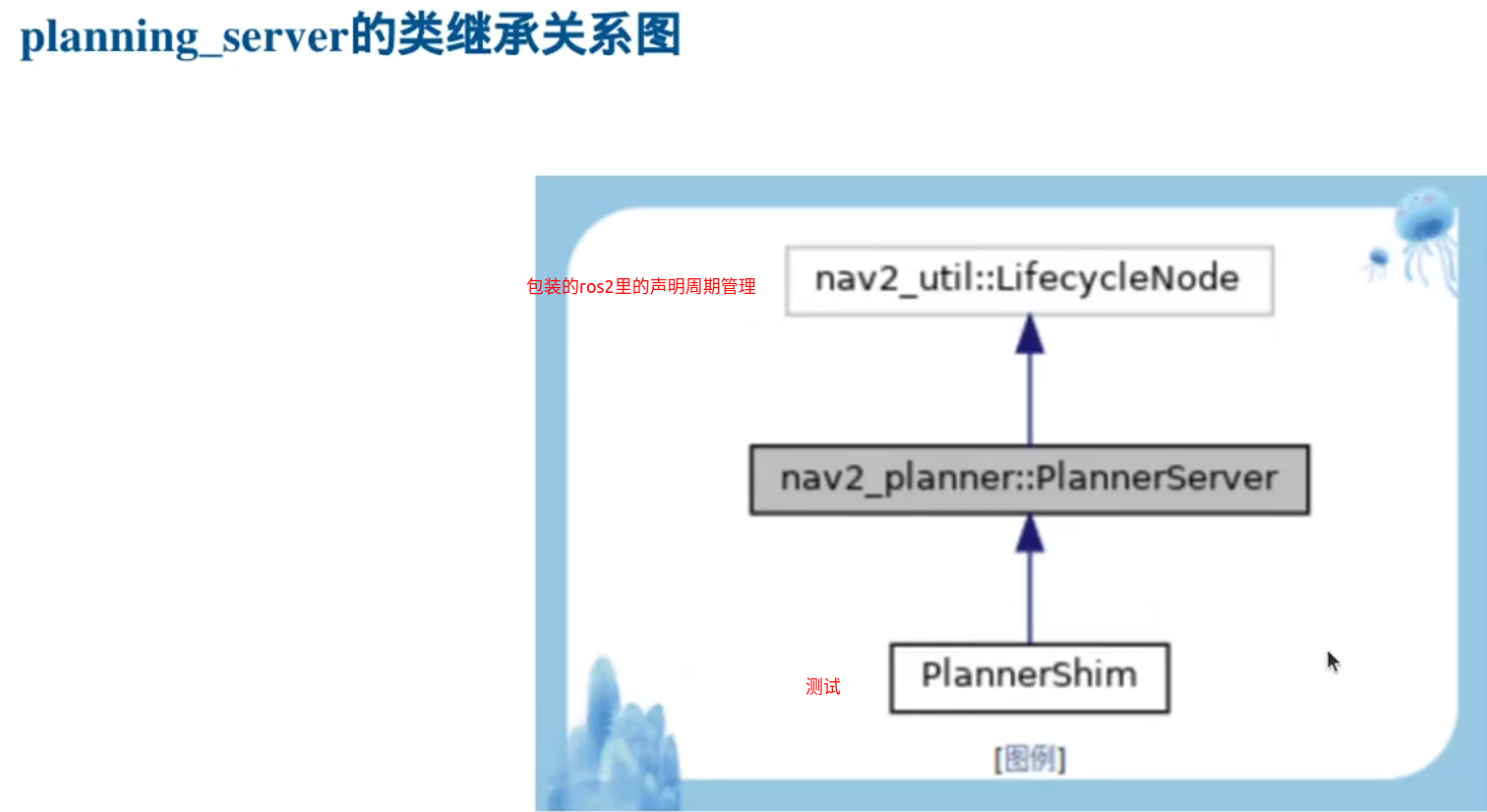
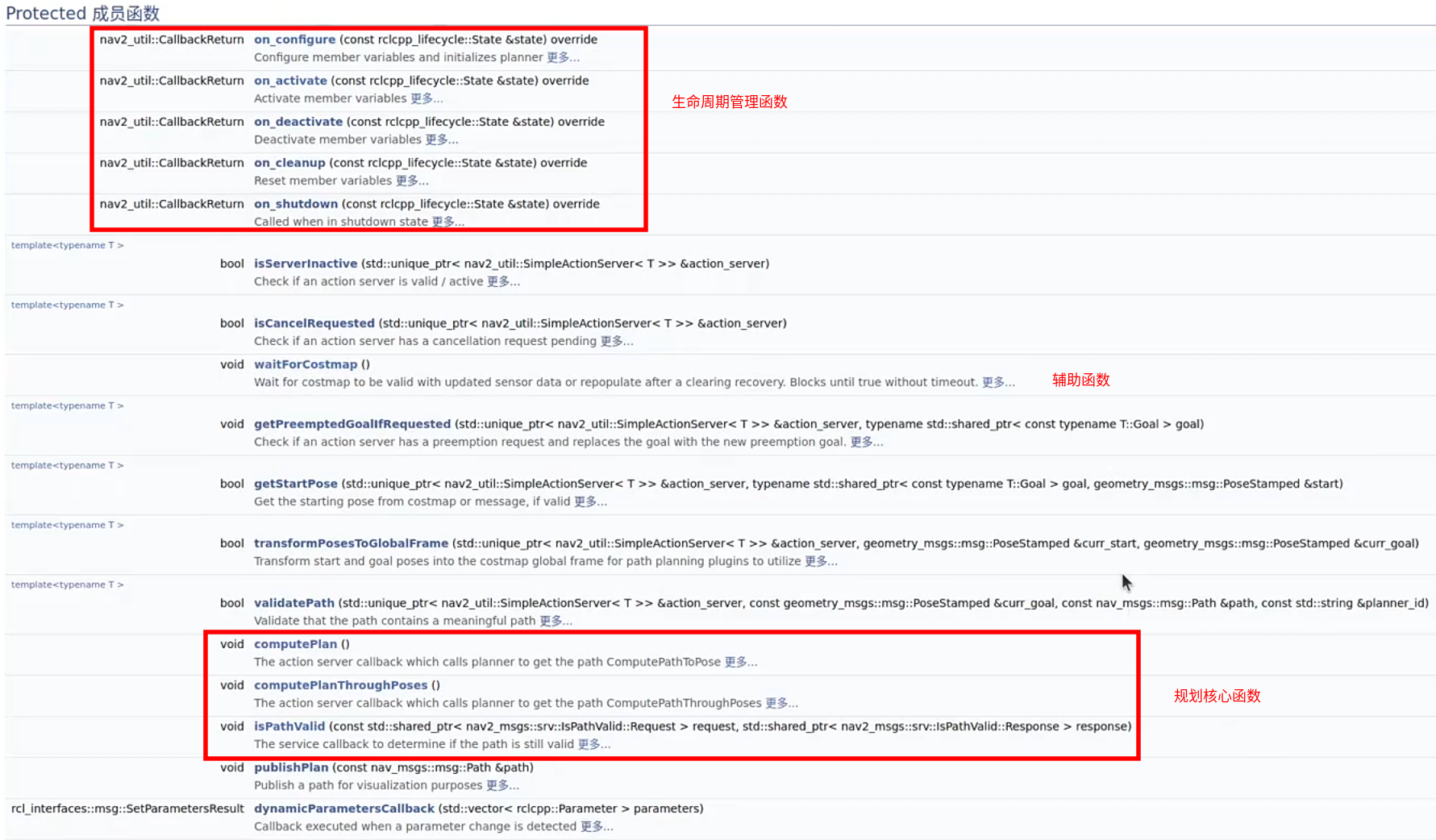
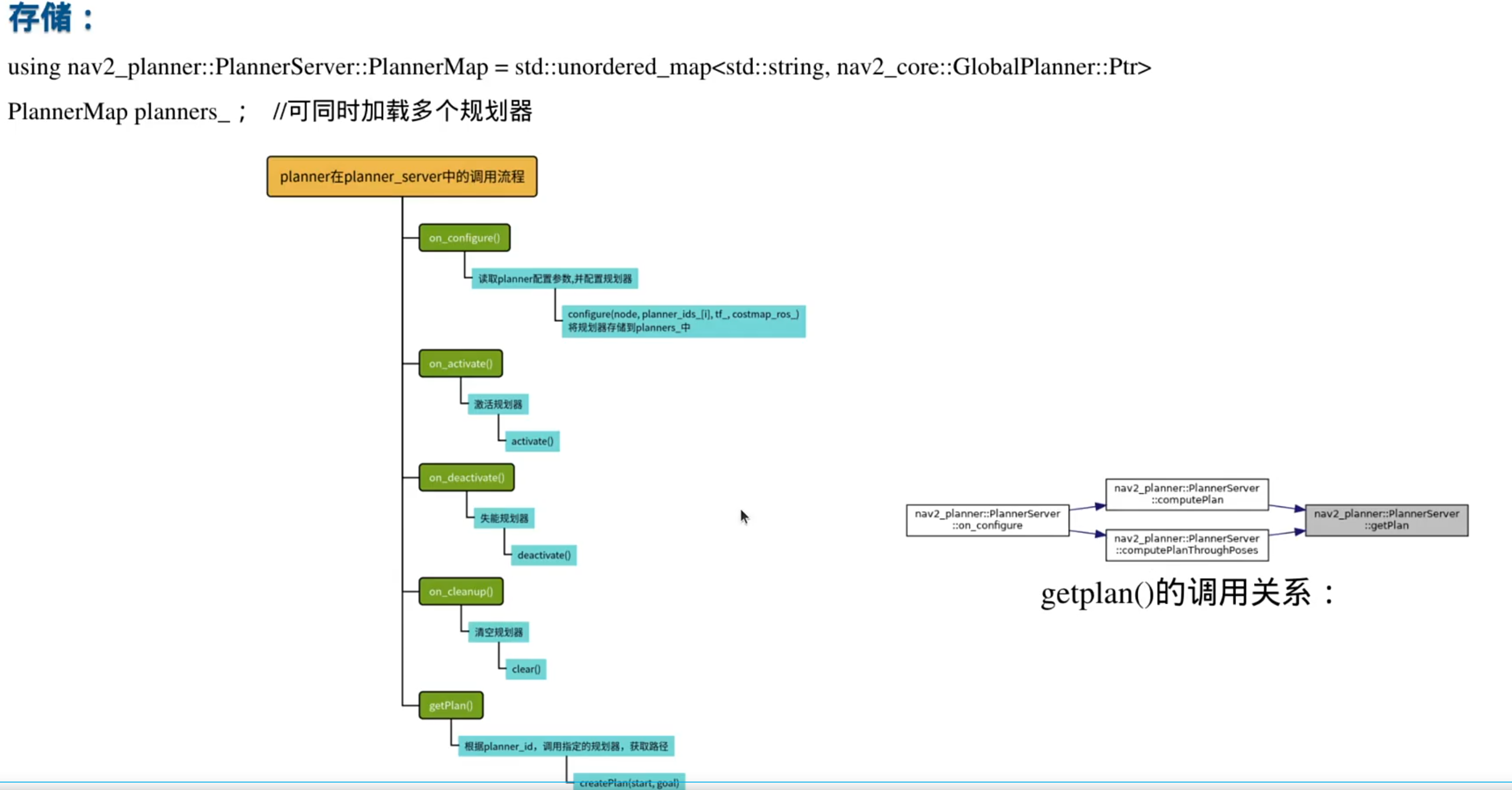
planner_server参数配置

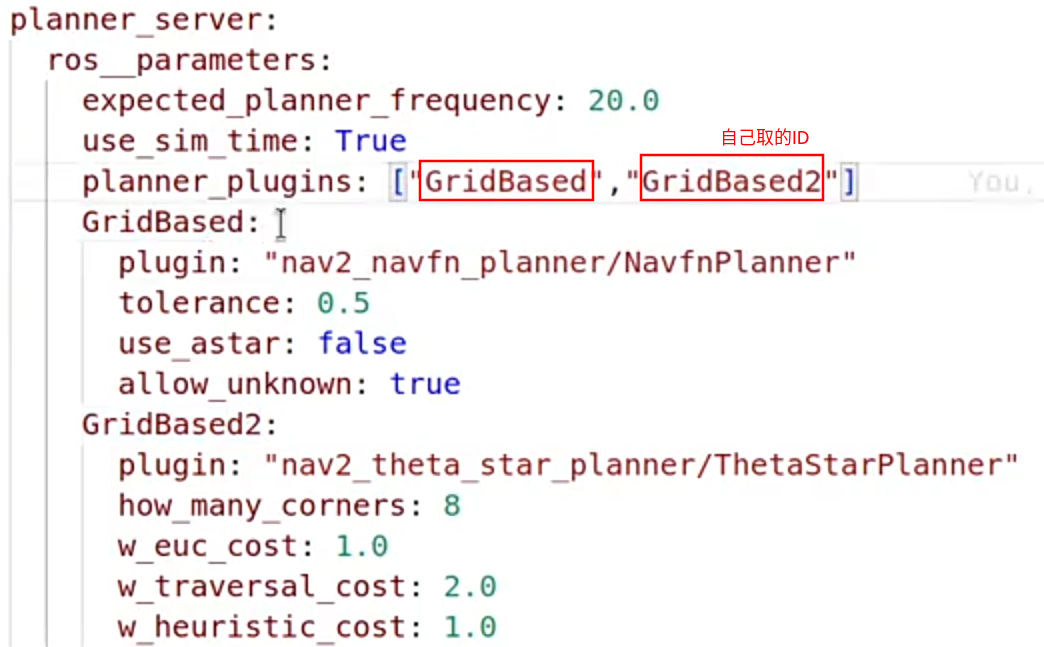
Controller_Server

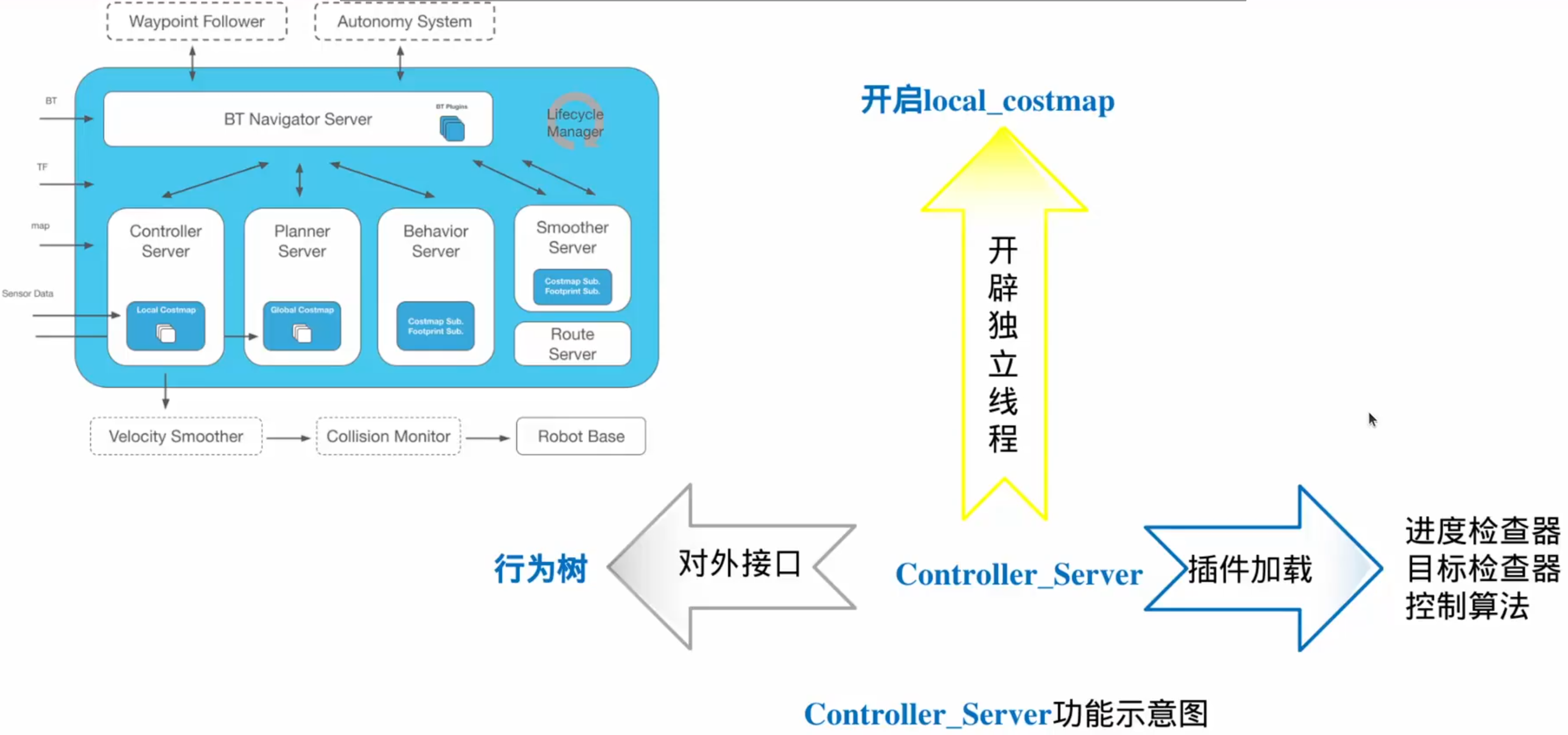
1.接口回调函数（给行为树调用）

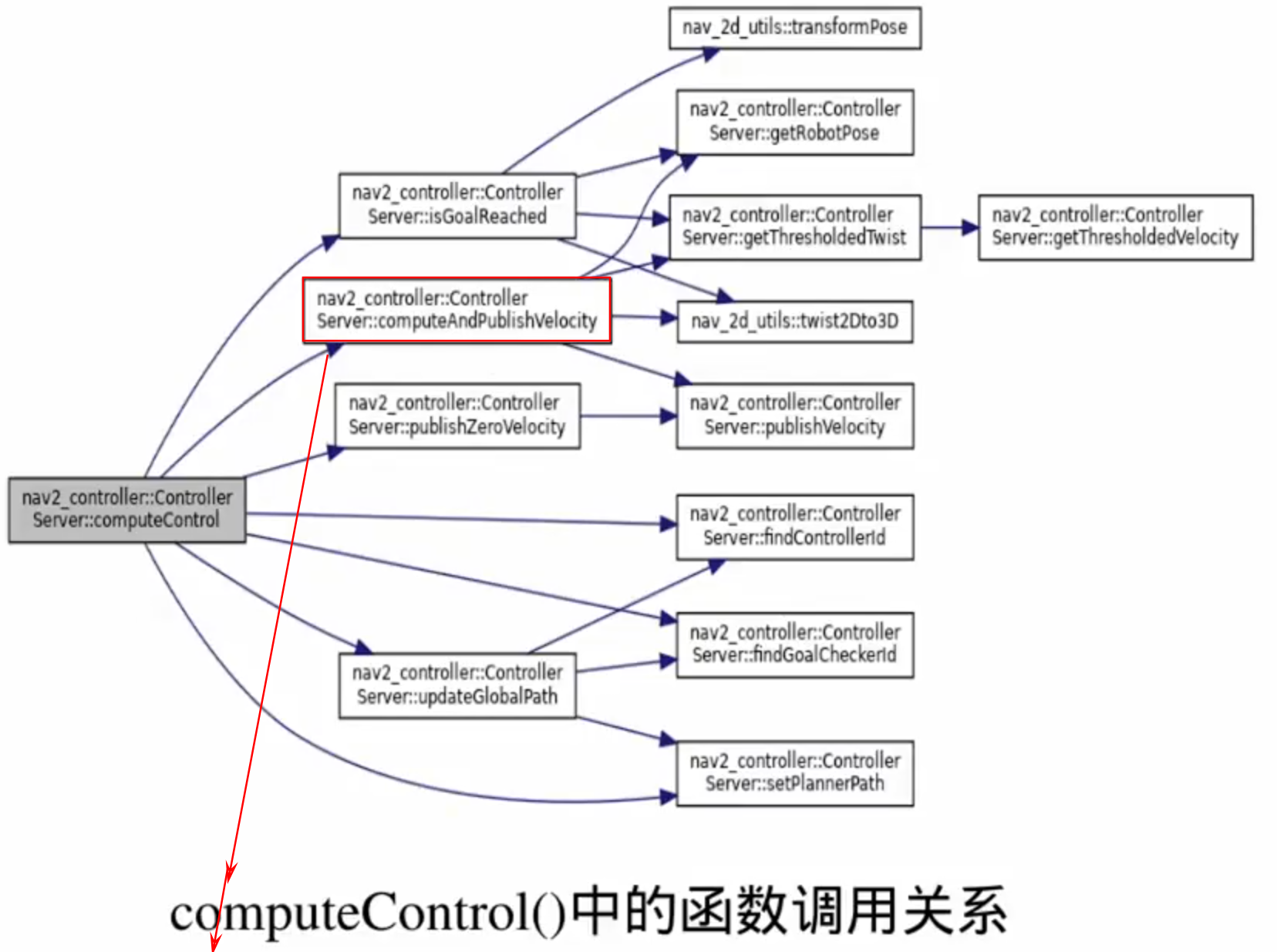
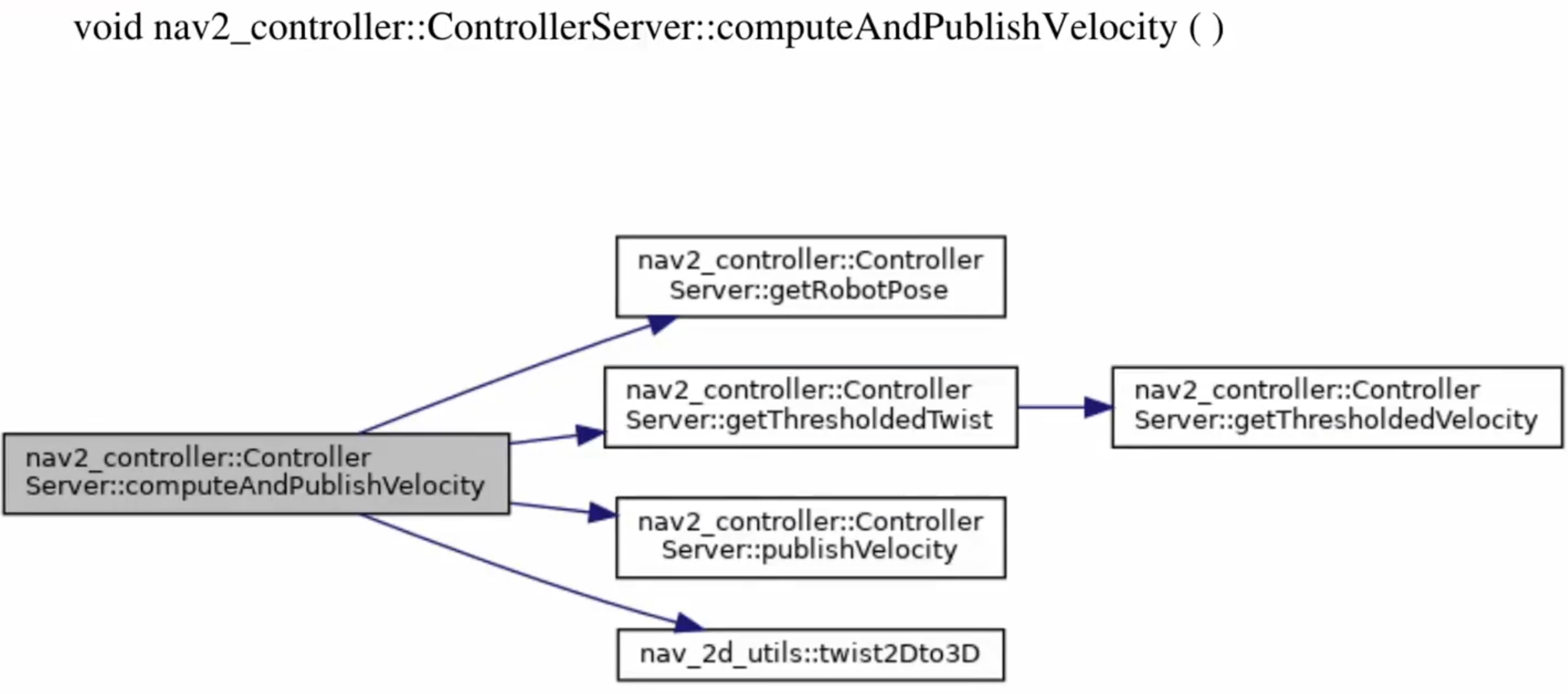
2.控制器插件

重要插件–进度检查器

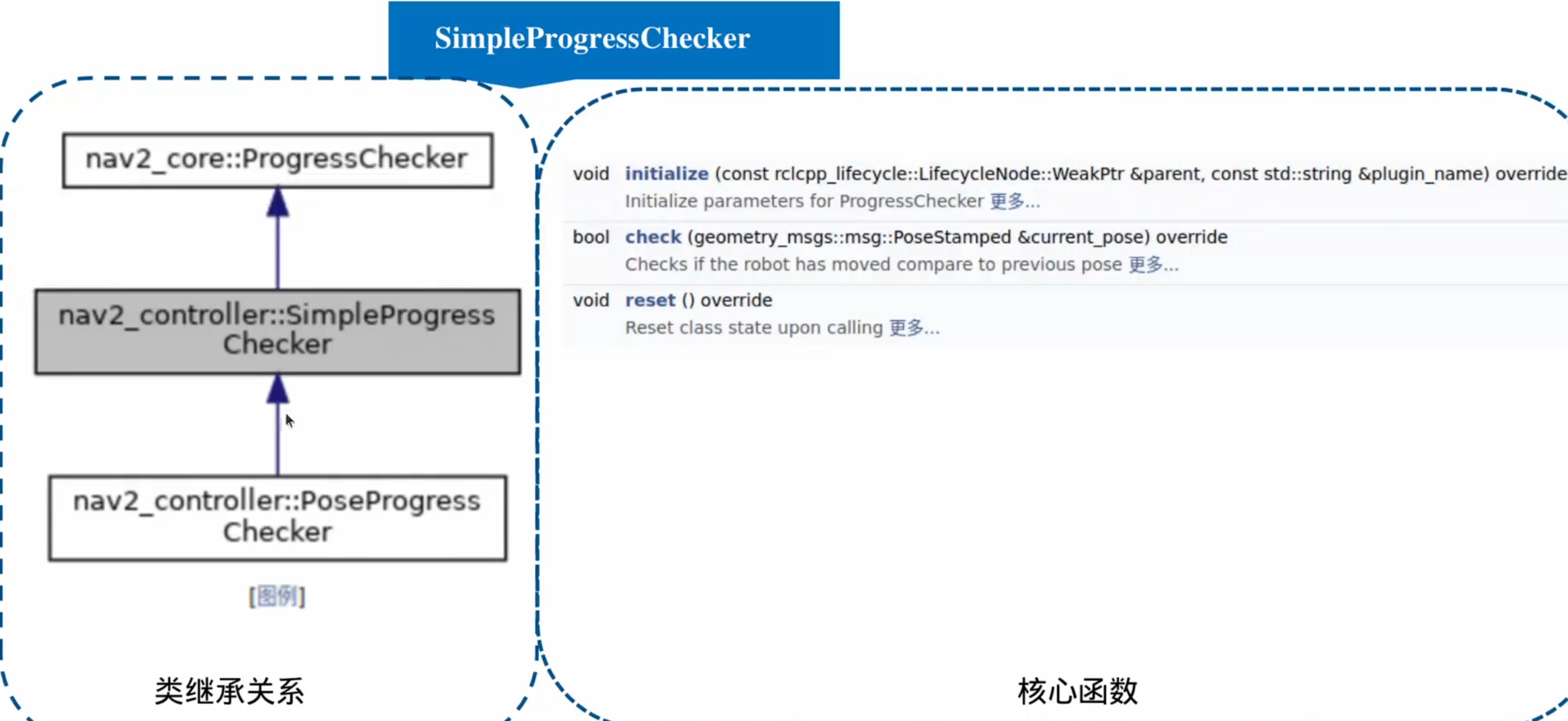
重要插件–目标检查器

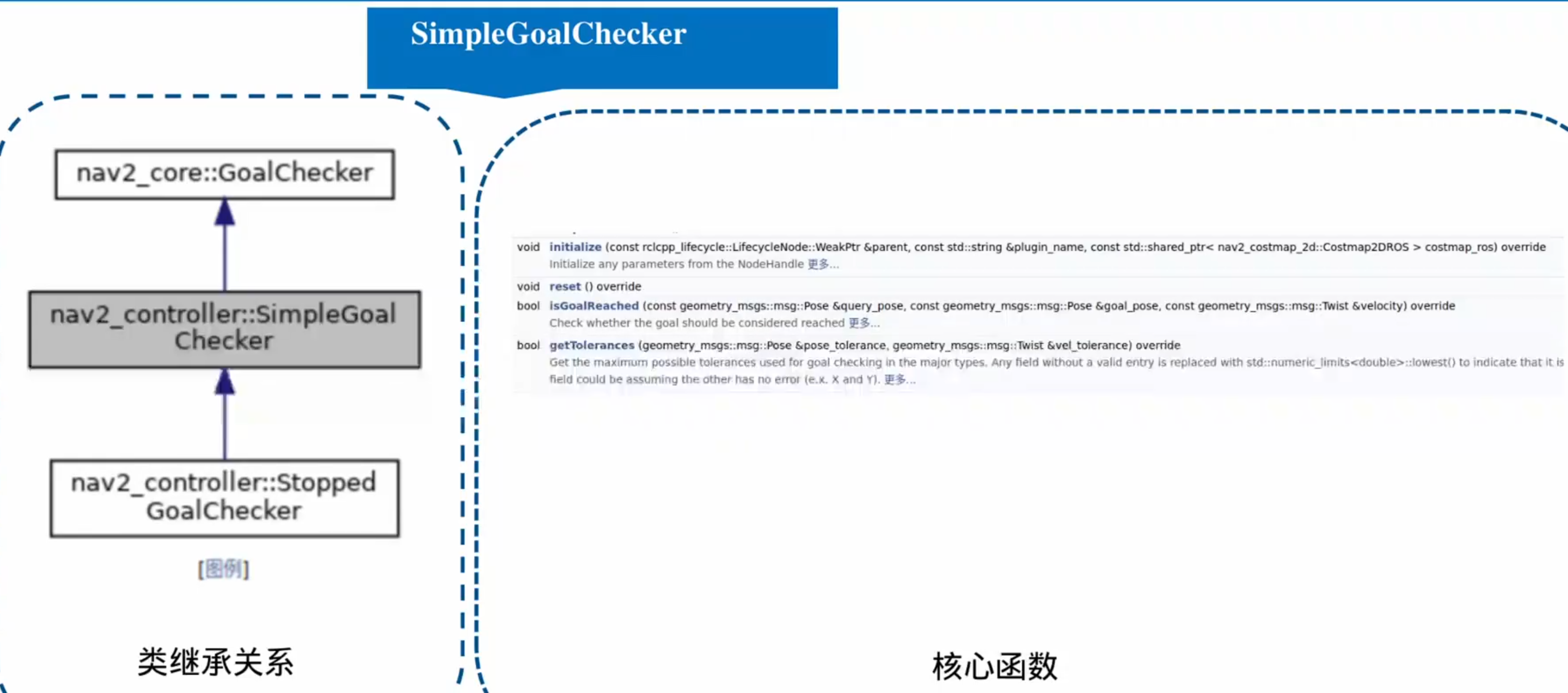
控制流程：

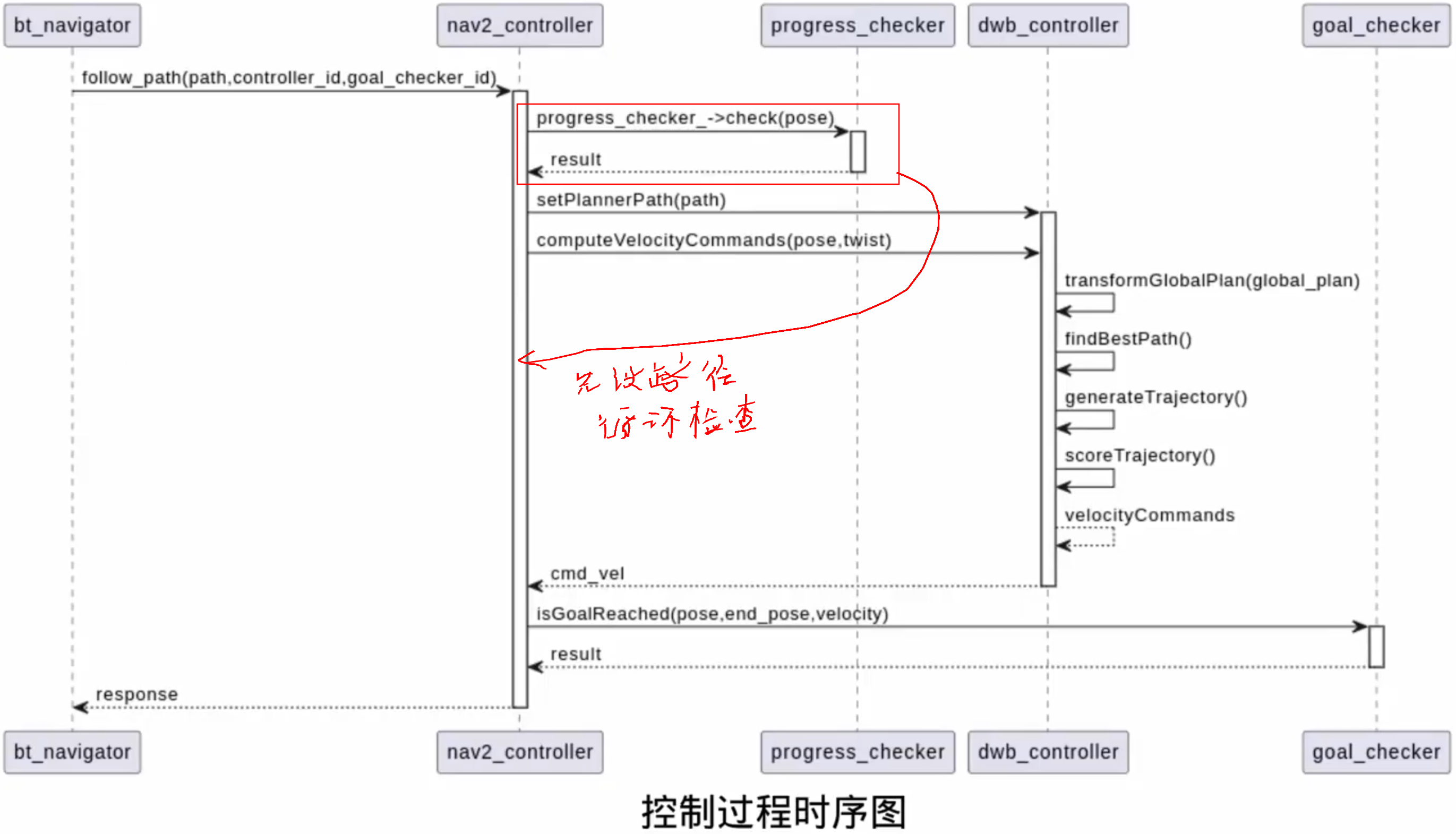
3.开启局部代价地图

和Planner_Server类似

DWB算法详解

2024-10-12

Realsense

pyrealsense.core module

pyrealsense.core.Device(service, device_id=0, streams=None, depth_control_preset=None, ivcam_preset=None)

class pyrealsense.core.DeviceBase(dev, device_id, name, serial, version, streams)

class pyrealsense.core.Service

pyrealsense.stream module

2024-10-11

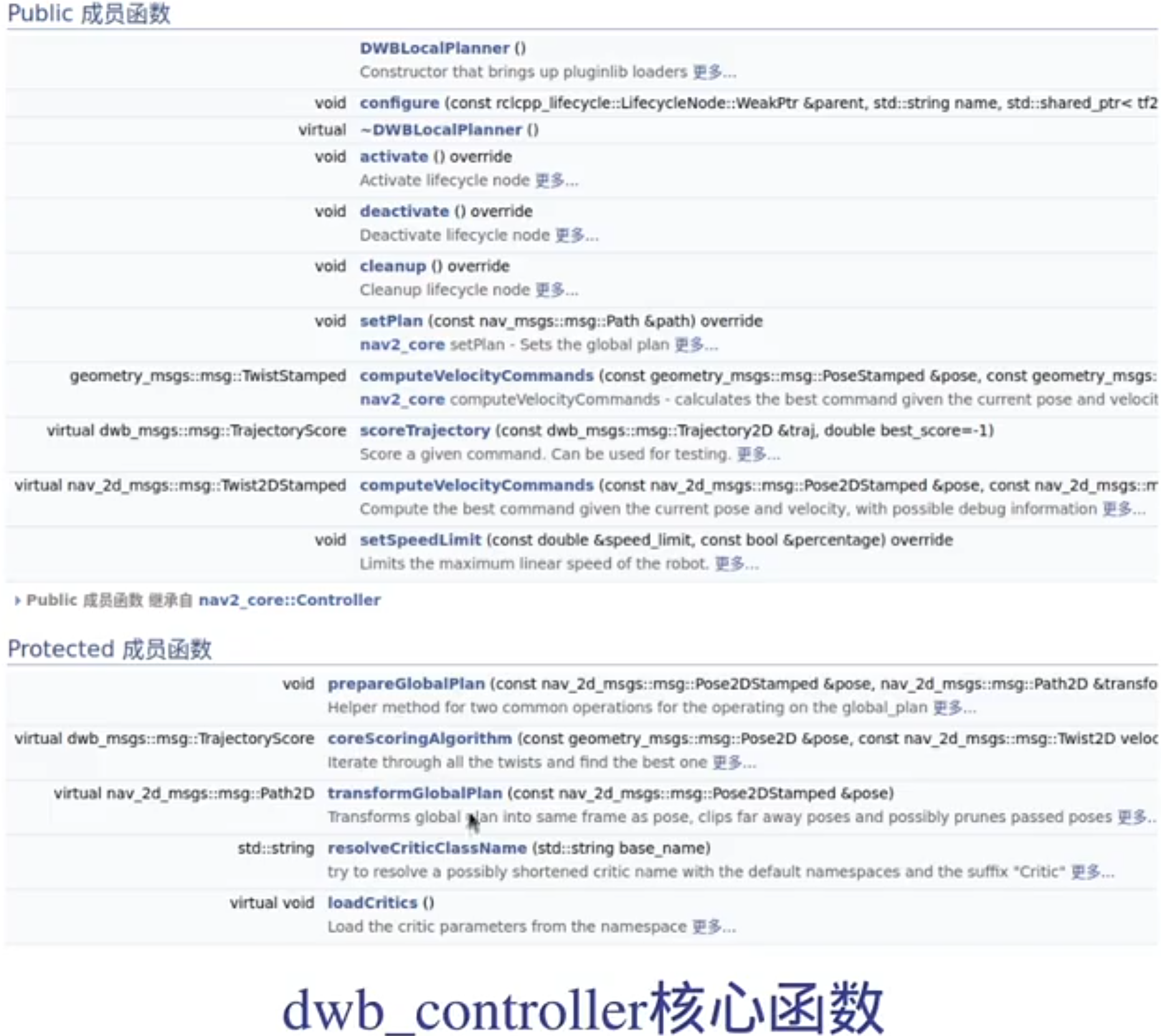
C++STL

STL 即标准模板库（Standard Template Library），是 C++ 标准库的一部分，里面包含了一些模板化的通用的数据结构和算法。由于其模板化的特点，它能够兼容自定义的数据类型，避免大量的造轮子工作。NOI 和 ICPC 赛事都支持 STL 库的使用，因此合理利用 STL 可以避免编写无用算法，并且充分利用编译器对模板库优化提高效率。

Boost 是除了标准库外，另一个久副盛名的开源 C++ 工具库，其代码具有可移植、高质量、高性能、高可靠性等特点。Boost 中的模块数量非常之大，功能全面，并且拥有完备的跨平台支持，因此被看作 C++ 的准标准库。C++ 标准中的不少特性也都来自于 Boost，如智能指针、元编程、日期和时间等。尽管在 OI 中无法使用 Boost，但是 Boost 中有不少轮子可以用来验证算法或者对拍，如 Boost.Geometry 有 R 树的实现，Boost.Graph 有图的相关算法，Boost.Intrusive 则提供了一套与 STL 容器用法相似的侵入式容器。

STL 容器

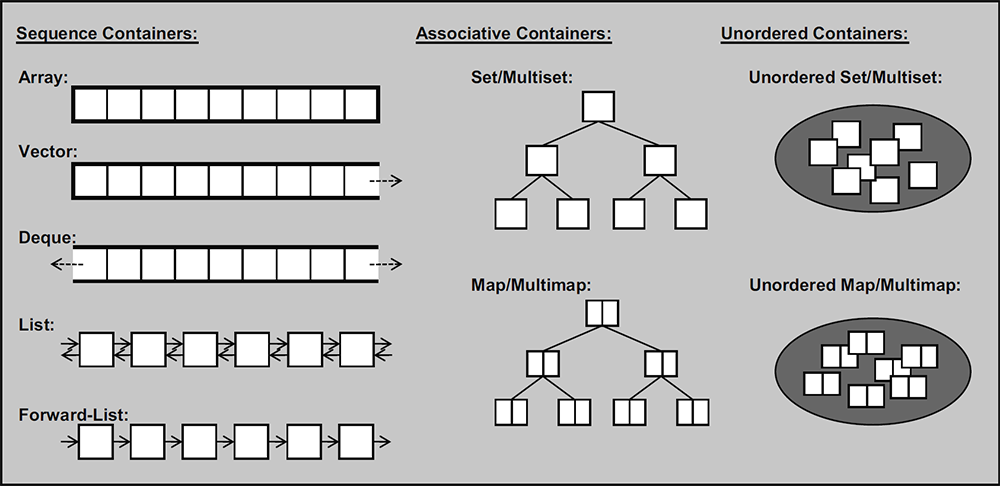
分类：

1. ==序列式==容器

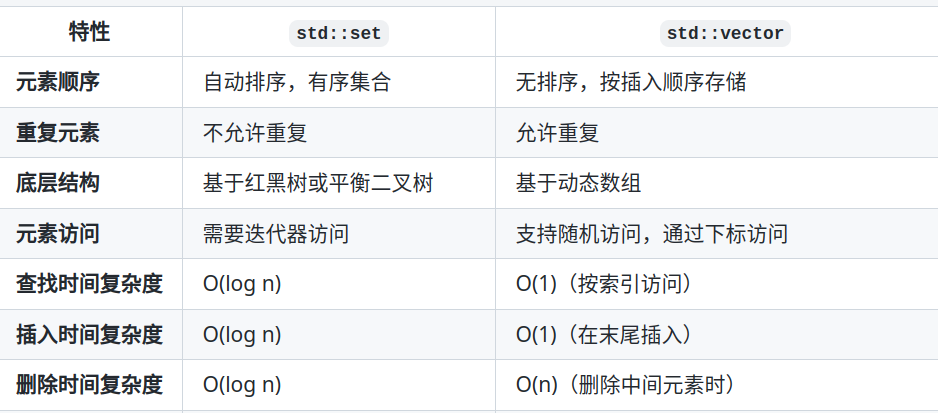
vector(向量)后端可高效增加元素的顺序表.
array(数组)，定长的顺序表。
deque（双端队列）双端可高效增加元素的顺序表。
list（列表）可以沿双向遍历的链表。
forward_list（单向列表）只能沿一个方向遍历的链表。

2，==关联式==容器

set（集合）有序储存互异元素的容器
- 不允许重复元素。存储唯一的元素，且自动按升序排序。
- 元素的插入、删除和查找操作的时间复杂度为O(log n)。
multiset(多重集合)允许存储重复的元素，且也会自动按升序排序
- 允许重复元素。
- 与set类似，插入、删除和查找操作的时间复杂度同样为O(log n)。
map（映射）由{建，值}对组成的集合（也是集合）
- 唯一性：每个键只能出现一次；如果插入一个已存在的键，则会更新其对应的值。
- 有序性：map中的元素会根据键自动排序，默认情况下是升序排列。
- 时间复杂度：插入、删除和查找操作的平均时间复杂度为O(log n)。

3，无序(并联式)容器

无序（多重）集合(unordered_set/unordered_multiset)C++11，与 set/multiset 的区别在于元素无序，只关心「元素是否存在」，使用哈希实现。
- 唯一性：unordered_set 中的每个元素都是唯一的，不能重复。
- 无序性：元素的排列是基于哈希值的，不按照任何特定顺序存储。
- 性能：插入、查找和删除操作的平均时间复杂度为 O(1)，但在最坏情况下可能会退化为 O(n)
无序（多重）映射(unordered_map/unordered_multimap)C++11，与 map/multimap 的区别在于键 (key) 无序，只关心 “键与值的对应关系”，使用哈希实现。

容器适配器

容器适配器其实并不是容器。它们不具有容器的某些特点（如：有迭代器、有 clear() 函数……）。

「适配器是使一种事物的行为类似于另外一种事物行为的一种机制」，适配器对容器进行包装，使其表现出另外一种行为。

栈(stack) 后进先出 (LIFO) 的容器，默认是对双端队列（deque）的包装。
队列(queue) 先进先出 (FIFO) 的容器，默认是对双端队列（deque）的包装。
优先队列(priority_queue) 元素的次序是由作用于所存储的值对上的某种谓词决定的的一种队列，默认是对向量（vector）的包装。

容器声明

都是 containerName<typeName,...> name 的形式，但模板参数（<> 内的参数）的个数、形式会根据具体容器而变。

本质原因：STL 就是「标准模板库」，所以容器都是模板类。

容器共有函数

= ：赋值运算符，赋值构造函数

begain() :返回指向开头元素的迭代器

end（）：返回指向末尾的下一个元素的迭代器。end() 不指向某个元素.end() 迭代器指向的是一个“哨兵”位置，表示容器的结束。可以用来判断迭代是否完成。

size():返回容器内的元素个数

max_size()：返回容器理论上能存储的最大元素个数。依容器类型和所存储变量的类型而变。

empty()：返回容器是否为空。

swap()：交换两个容器。

clear()：清空容器。

==/!=/</>/<=/>=：按 字典序 比较两个容器的大小.无序容器不支持 </>/<=/>=。

`priority_queue<int, vector<int>, greater<int>>` 解析

priority_queue<int>:
- priority_queue 是 C++ STL（标准模板库）中的一个容器适配器，用于实现优先队列。
- 优先队列是一个特殊的队列，元素总是按优先级顺序被访问，优先级高的元素总是先被取出。
- 默认情况下，priority_queue 使用 最大堆（即，优先队列中最优先的元素是当前堆中的最大元素）。
vector<int>:
- 这部分指定了 priority_queue 内部使用的底层容器。默认情况下，priority_queue 使用一个 vector 来存储元素。
- vector<int> 表示优先队列会存储 int 类型的元素，并且底层数据结构是一个动态数组（vector）。
greater<int>:
- greater<int> 是一个函数对象（比较器），它指定了如何比较队列中的元素。
- greater<int> 表示一个 升序比较器，即它会把 较小的元素优先 放到队列前面。
- 默认情况下，priority_queue 是一个最大堆，它是通过 less<int>（即大于比较）来实现的，而 greater<int> 则实现了一个最小堆（即小于比较）。这使得 pq 中的元素会按照从小到大的顺序排列。

为什么 `std::sort` 必须在 `std::unique` 之前使用？

std::unique 只能去除相邻的重复元素。它不会去除容器中所有不相邻的重复元素。例如，假设容器中有 1, 2, 3, 1, 4, 5, 1，如果在调用 std::unique 之前没有对容器排序，std::unique 将无法去除所有重复元素，因为它只会处理相邻的元素。因此，为了确保所有重复元素都能被去除，必须先对容器进行排序，使得相同的元素排列在一起，然后才能通过 std::unique 去除它们。

a[n]

std::sort(a,a+n);

m = std::unique（a,a+n）-n;

std::cin 输入流（空格分割）

stringstream 字符串流

begain（），end（）

vector<>

clear() , resize() , push_back() , pop_back() , empty() ，可重复

set<>

自动排序：默认升序

不可重复

不可修改

insert（），find（），count（）， erase（），empty（）

stack<>

priority_queue<>

push() ,pop() ,top()

queue

push() ,pop() ,front()

ctrl + tab + 上下左右代替鼠标切换文件

Ctrl + W：一个字符、一个字符串、一行、两行代码逐渐扩选

Alt + Shift + 左键：针对要编辑的部分快速选中多行

std::advance(iter, n);

如果 n 为正数，迭代器会向前移动；如果 n 为负数，迭代器会向后移动。

yoloV8-segment模型安卓端部署

一.模型转换：best.pt——>yolov8n-seg.bin和yolov8n-seg.param

1. build ncnn

2. convert yolov8 pt ->ONNX

3. onnx2ncnn

ONNX介绍

4. 但是也会闪退！！！

5. 重新执行3，4步操作

二. 模型转换完毕，下面开始使用Android studio构建安卓工程

1. Configure ncnn

2. Configure OpenCV

3. Android studio构建

三、构建，烧录

结果分析：

四、模型量化

结果分析：

完毕！！

3.2

4.2

5.1

5.2

5.4

5.5

6

基于模型预测控制与全身控制的控制器

虚拟模型控制（VMC: Virtual Model Control）

全身控制（WBC）

WBC 使用了浮动基逆动力学

激光雷达

Virtual RobotX (VRX)

Webots水下机器人仿真

uuv_simulator水下机器人仿真

[旋转矩阵，欧拉角，四元数，旋转向量和齐次变换矩阵]

name="urdf_spawner"

respawn="false"

output="screen"

举例说明

视口裁剪（Viewport Clipping）

透视裁剪（Perspective Clipping）

总结

坐标变换流程

NDC 到屏幕空间的转换

虚函数（Virtual Function）

纯虚函数（Pure Virtual Function）

line.compare(0, 2, "v ") 的含义：

平面和场景

原始代码：

修改后的代码：

问题分析：

1. count++ 是非原子操作

2. ++count 是原子操作

3. 存储递增结果到 n

线程安全与性能考虑：

一种有趣的搜索思路：JPS

从容应对动态障碍物–D*（动态A星算法）

lattice planner

轨迹跟踪

Nav2中的地图

配置参数

全局路径规划服务器

planner_server参数配置

Controller_Server

DWB算法详解

pyrealsense.core module

pyrealsense.stream module

STL 容器

分类：

1. ==序列式==容器

2，==关联式==容器

3，无序(并联式)容器

容器适配器

容器声明

容器共有函数

priority_queue<int, vector<int>, greater<int>> 解析

为什么 std::sort 必须在 std::unique 之前使用？

`name="urdf_spawner"`

`respawn="false"`

`output="screen"`

`line.compare(0, 2, "v ")` 的含义：

1. `count++` 是非原子操作

2. `++count` 是原子操作

3. 存储递增结果到 `n`

`priority_queue<int, vector<int>, greater<int>>` 解析

为什么 `std::sort` 必须在 `std::unique` 之前使用？