
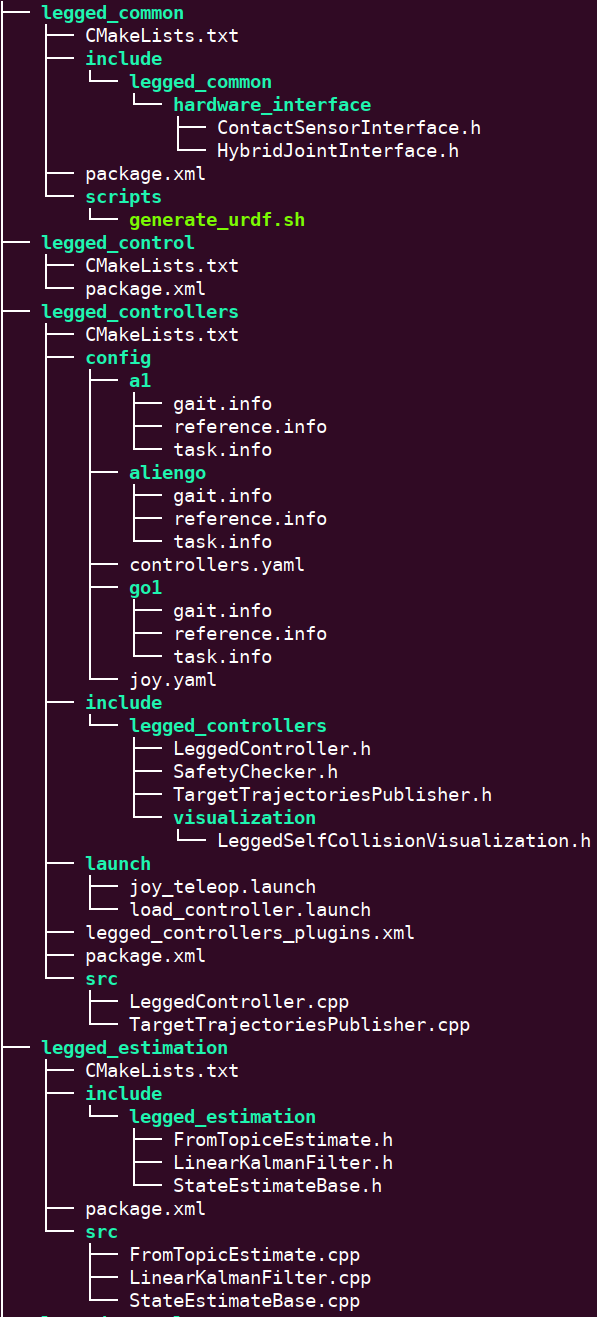
legged_control
基于OCS2和ros-controls的非线性MPC 1与WBC框架
- docs - 包含项目文档和说明。
- legged_common - 共享的数据结构和函数库。
- legged_control - 主控制堆栈的源码,实现了NMPC和WBC的核心算法。
- legged_controllers - 控制器的具体实现,如腿部运动模式控制器。
- legged_estimation - 估计相关的组件,可能涉及状态估计或传感器数据处理。
- legged_examples - 示例代码,可能含有特定机器人的示例配置或仿真设置。
- legged_gazebo - Gazebo仿真相关文件,用于虚拟环境中测试机器人。
- legged_hw - 硬件交互层,用于实际机器人的控制。
- legged_interface - 提供与机器人交互的API。
- legged_wbc - Whole Body Control的相关代码。
- qpoases_catkin - 可能是作为依赖项的QPOASES求解器的ROS集成。
Ubuntu 20.04
ROS noetic
catkin
OCS2 是一个针对切换系统优化控制的 C++ 工具箱,适用于机器人任务,包括路径约束处理和 URDF 模型支持。它提供了高效算法如 SLQ、iLQR 和 SQP,并具有 ROS 接口。工具箱包含自动微分工具,确保在有限计算能力的机器人应用中实现数值稳定和高效控制。
OCS2是一个大型单库项目;请不要尝试编译整个仓库。
URDF文件和YAML文件通常在 ROS 启动文件中被调用。具体步骤如下:
URDF 文件:
- 在启动文件(
.launch)中使用<param>标签将 URDF 文件加载到参数服务器:<param name="robot_description" command="$(find xacro)/xacro $(find your_package)/urdf/your_robot.urdf.xacro"/>
- 在启动文件(
YAML 文件:
- 也可以在启动文件中使用
<rosparam>标签加载 YAML 文件:<rosparam file="$(find your_package)/config/your_config.yaml" command="load"/>
- 也可以在启动文件中使用
节点中访问:
- 在你的 ROS 节点代码中,可以通过
ros::param::get()或ros::NodeHandle来访问这些参数。
- 在你的 ROS 节点代码中,可以通过
这样,URDF 和 YAML 文件就能在你的 ROS 项目中被有效地调用和使用。
<geometry> <!--几何形状-->
<inertial> <!--惯性属性-->
<joint name="world_to_slideBar" type="fixed"> <!--这个关节用于将 slideBar 固定在世界坐标系中的特定位置,使得它在仿真中保持稳定,提供支撑作用。-->
<parent link="world"/>
<child link="slideBar"/>
<origin xyz="0.0 0.0 2.0"/>
</joint>
<gazebo reference="slideBar">
- Gazebo特定属性: 用于指定该链接在 Gazebo 中的特性。
<mass value="0.1"/>
- 质量: 指定了链接的质量为 0.1 千克
<origin> 位置
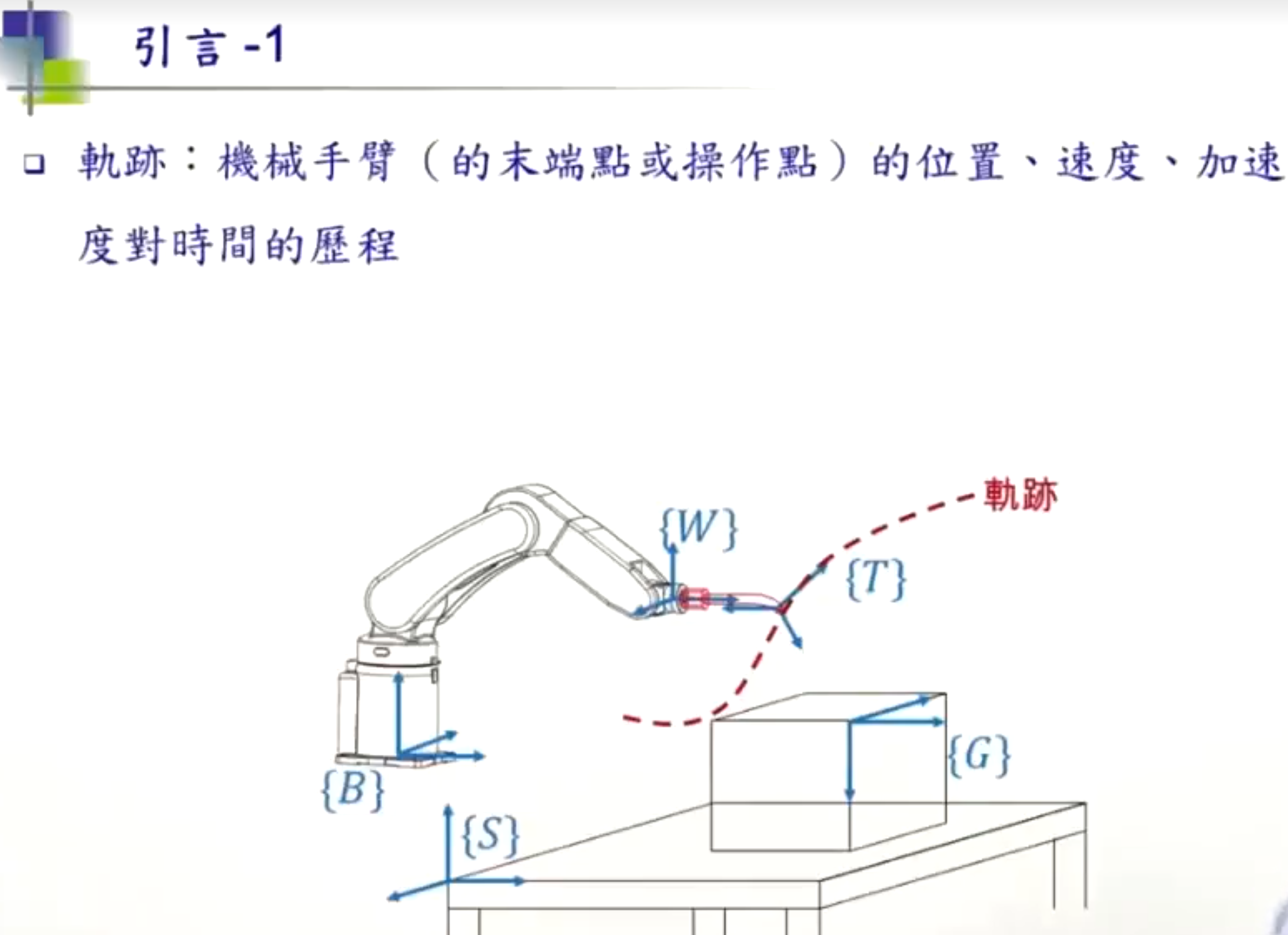
自由度通俗的讲就是为了唯一确定一个机构的运动状态所必须的独立变量的个数
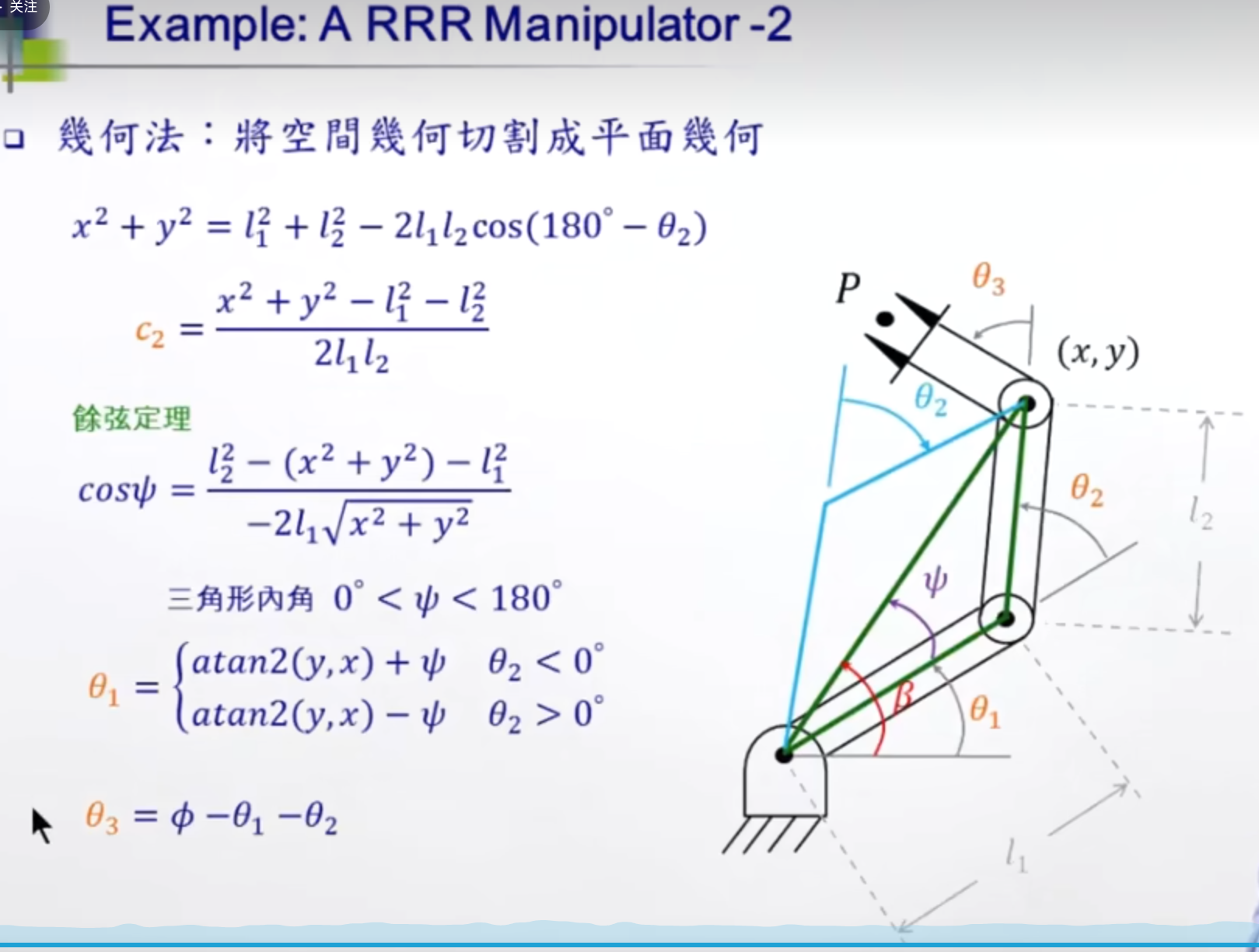

c12=cos(seta1+seta2 )



<joint name="base_to_plat" type="prismatic">
<axis xyz="1 0 0"/>
<origin xyz="0.0 0.0 0.0"/>
<parent link="slideBar"/>
<child link="cart"/>
<limit effort="100000.0" lower="-15" upper="15" velocity="100"/>
<dynamics damping="0.0" friction="0.0"/>
</joint>
是什么意思
这段代码定义了一个名为 base_to_plat 的滑动关节(prismatic joint),其主要功能是让 cart 在 slideBar 上进行线性滑动。以下是对每个部分的详细解释:
1. <joint name="base_to_plat" type="prismatic">
- 名称和类型:
name="base_to_plat": 该关节的名称是base_to_plat。type="prismatic": 关节类型为滑动关节,允许连接的部分沿一个轴线性移动。
2. <axis xyz="1 0 0"/>
- 运动轴:
xyz="1 0 0": 表示滑动关节的运动轴为 X 轴。1表示在 X 方向上有运动,而 Y 和 Z 方向上没有运动。
3. <origin xyz="0.0 0.0 0.0"/>
- 原点位置:
xyz="0.0 0.0 0.0": 该关节的原点位置设置在 (0, 0, 0),通常是关节的中心点。
4. <parent link="slideBar"/>
- 父链接:
link="slideBar": 指定slideBar是该关节的父链接。也就是说,cart相对于slideBar移动。
5. <child link="cart"/>
- 子链接:
link="cart": 指定cart是该关节的子链接。表示cart将通过该关节的运动影响到。
6. <limit effort="100000.0" lower="-15" upper="15" velocity="100"/>
- 运动限制:
effort="100000.0": 该关节能够承受的最大力为 100,000(单位通常为牛顿)。lower="-15": 关节的最小位置限制为 -15(单位通常为米),表示cart可以向后滑动的最大距离。upper="15": 关节的最大位置限制为 15(单位通常为米),表示cart可以向前滑动的最大距离。velocity="100": 关节的最大速度为 100(单位通常为米/秒),表示cart的移动速度限制。
7. <dynamics damping="0.0" friction="0.0"/>
- 动力学属性:
damping="0.0": 阻尼系数为 0,表示没有额外的阻力影响滑动。friction="0.0": 摩擦系数为 0,表示在滑动过程中没有摩擦力。
总结
这段代码的主要目的是定义一个滑动关节,使得 cart 可以在 X 轴上滑动,受到的限制和动力学特性被明确设定。这在机器人和机械模拟中是非常重要的,可以精确控制其运动行为。
<transmission name="tran2">
<type>transmission_interface/SimpleTransmission</type>
<joint name="base_to_plat">
<hardwareInterface>hardware_interface/EffortJointInterface</hardwareInterface>
</joint>
<actuator name="planar_motor_2">
<hardwareInterface>hardware_interface/EffortJointInterface</hardwareInterface>
<mechanicalReduction>1</mechanicalReduction>
</actuator>
</transmission>
是什么意思
这段代码定义了一个名为 tran2 的传动系统,主要用于连接一个滑动关节和一个执行器。以下是各部分的解释:
1. <transmission name="tran2">
- 传动系统名称: 这个传动系统被命名为
tran2。
2. <type>transmission_interface/SimpleTransmission</type>
- 传动类型: 使用简单传动接口,表明传动的实现相对直接。
3. <joint name="base_to_plat">
- 关节连接: 连接到先前定义的滑动关节
base_to_plat。
4. <hardwareInterface>hardware_interface/EffortJointInterface</hardwareInterface>
- 硬件接口: 该关节使用的是努力关节接口,意味着通过施加力来控制关节运动。
5. <actuator name="planar_motor_2">
- 执行器名称: 该传动系统连接的执行器名为
planar_motor_2。
6. <mechanicalReduction>1</mechanicalReduction>
- 机械减速比: 设置为 1,表示执行器的输出与输入之间没有减速,直接传递力。
总结
整体上,这段代码用于定义一个简单的传动系统,将滑动关节和电机连接起来,以便通过施加力来控制滑动运动。
JointState 消息内容
JointState 消息通常包含以下字段:
name: 存储关节名称的字符串数组。position: 存储每个关节当前角度或位置的浮点数数组。velocity: 存储每个关节当前速度的浮点数数组。effort: 存储每个关节当前力矩或用力程度的浮点数数组。

LQR(线性二次调节器,Linear Quadratic Regulator)是一种用于控制系统的优化方法。它旨在通过最小化某个代价函数来设计控制器,通常用于线性动态系统。
LQR 的基本公式
假设有一个线性系统描述为:
$ \dot{x} = Ax + Bu $
其中:
- ( x ) 是状态向量
- ( u ) 是控制输入
- ( A ) 和 ( B ) 是系统矩阵
LQR 通过最小化以下代价函数来设计控制器:
$ J = \int_0^{\infty} (x^T Q x + u^T R u) , dt $
其中:
- ( Q ) 是状态权重矩阵,通常是半正定的$(Q \geq 0 )$
- ( R ) 是控制输入权重矩阵,通常是正定的($ R > 0 $)
最优控制律
通过求解代价函数的最小值,可以得到最优控制律:
$ u = -Kx $
其中 $K $是增益矩阵,通过以下公式计算:
$K = R^{-1} B^T P $
而$ P $ 是 Riccati 方程的解:
$A^T P + PA - PBR^{-1}B^T P + Q = 0 $
总结
LQR 方法通过设计一个控制器,最小化系统状态和控制输入的加权平方和,从而实现对线性系统的有效控制。它广泛应用于工程、自动控制、机器人等领域。
代码实现过程
在你提供的代码中,LQR控制器的设计过程主要包含以下几个步骤:
逆矩阵计算:
Eigen::Matrix<double, 1, 1> R_inv = R_.inverse();这里计算了控制输入权重矩阵 (R) 的逆。
计算 BRB 项:
Eigen::Matrix<double, 4, 4> BRB = B_ * R_inv(0, 0) * B_.transpose();这一步计算了 $BR^{-1}B^T$项,用于构建哈密尔顿矩阵。
构造哈密尔顿矩阵:
Eigen::Matrix<do uble, 8, 8> H; H.topLeftCorner(4, 4) = A_; H.topRightCorner(4, 4) = -BRB; H.bottomLeftCorner(4, 4) = -Q_; H.bottomRightCorner(4, 4) = -A_.transpose();哈密尔顿矩阵 (H) 是 LQR 解的核心部分,它结合了系统的动态矩阵 (A)、控制输入矩阵 (B) 和权重矩阵 (Q) 和 (R)。
特征值和特征向量计算:
Eigen::ComplexEigenSolver<Eigen::Matrix<double, 8, 8>> ces; ces.compute(H);通过计算哈密尔顿矩阵的特征值和特征向量来获取系统的稳定性信息。
选择稳定特征向量:
for (int i = 0; i < 8; ++i) { if (eigenvalues(i).real() < 0 && index < 4) { Vs.col(index) = eigenvectors.col(i); ++index; } }选择具有负实部的特征值对应的特征向量,以确保系统的稳定性。
解Ricatti方程:
Eigen::MatrixXcd P_c = Vs2 * Vs1.inverse(); Eigen::Matrix4d P = P_c.real(); // Take the real part通过特征向量计算 Riccati 方程的解 (P),这是 LQR 控制中的关键步骤。
计算 LQR 增益矩阵:
Eigen::Matrix<double, 1, 4> K_temp = R_inv(0, 0) * B_.transpose() * P; return K_temp.transpose();最后计算控制增益矩阵 (K),该矩阵用于生成控制输入。
总结
LQR 控制器的实现通过构造哈密尔顿矩阵,计算其特征值和特征向量,求解 Riccati 方程,最终得到一个最优控制增益 (K)。通过这种方式,LQR 能够有效地平衡系统的性能和控制输入,以保证系统的稳定性和响应速度。
Eigen::MatrixXd 和 Eigen::Matrix4d 是 Eigen 库中用于表示矩阵的两种不同类型。它们的主要区别如下:
1. 尺寸
Eigen::MatrixXd:- 这是一个动态大小的矩阵,表示一个任意大小的矩阵。
- 在运行时可以根据需要动态调整其行数和列数。
Eigen::Matrix4d:- 这是一个固定大小的矩阵,专门表示一个 4x4 的矩阵。
- 行数和列数在编译时就已经确定,不能被更改。
2. 内存管理
Eigen::MatrixXd:- 由于是动态大小,内存分配通常是在堆上进行管理,可能会有额外的开销。
Eigen::Matrix4d:- 由于大小固定,内存分配是静态的,通常在栈上分配,性能更高,尤其在小矩阵操作时。
3. 使用场景
Eigen::MatrixXd:- 适合处理不确定大小的矩阵,特别是在算法中需要处理各种尺寸的情况时。
Eigen::Matrix4d:- 适合处理明确为 4x4 矩阵的场景,如图形变换、旋转矩阵等。
###ubuntu上ros与anaconda冲突的最好解决办法:
catkin_make -DPYTHON_EXECUTABLE=/usr/bin/python3
下次再安装ros时,在anaconda环境里安装,要不然python混乱太搞了
现在有更好的方法:
export PATH="/usr/bin:$PATH"
zgh@zgh-Legion-Y7000P-IAH7:~/ROS_Projects/dog_gazebo$ which python
/usr/local/anaconda3/bin/python
zgh@zgh-Legion-Y7000P-IAH7:~/ROS_Projects/dog_gazebo$ which python3
/usr/local/anaconda3/bin/python3
zgh@zgh-Legion-Y7000P-IAH7:~/ROS_Projects/dog_gazebo$ sudo vim ~/.bashrc
zgh@zgh-Legion-Y7000P-IAH7:~/ROS_Projects/dog_gazebo$ source ~/.bashrc
zgh@zgh-Legion-Y7000P-IAH7:~/ROS_Projects/dog_gazebo$ which python3
/usr/bin/python3
zgh@zgh-Legion-Y7000P-IAH7:~/ROS_Projects/dog_gazebo$ which python
/usr/bin/python
zgh@zgh-Legion-Y7000P-IAH7:~/ROS_Projects/dog_gazebo$ python -V
Python 3.8.10
完美解決
[ERROR] [1728964010.917743989]: [registerPublisher] Failed to contact master at [localhost:11311]. Retrying…
只是roscore没开
在 MoveIt! 的 moveit_setup_assistant 中,配置规划组时的 Base Link 和 Tip Link 是指机器人模型中关节链的起始和结束部分。具体来说:
Base Link
- 定义: Base Link 是指关节链的起始位置,通常是机器人的“基础”或“根”部分。这通常是固定的、与机器人底座相连的链接。
- 作用: 它作为整个机器人运动的参考点,所有的运动都是相对于这个基准链接进行的。在机器人操作时,Base Link 通常是地面上的固定部分,负责提供稳定性。
Tip Link
- 定义: Tip Link 是指关节链的结束位置,它是规划组的最后一个链接。通常,这个链接表示执行器的末端,如机械手爪、工具或传感器等。
- 作用: Tip Link 是你希望 MoveIt! 进行运动规划的目标位置。通过指定 Tip Link,MoveIt! 可以计算从 Base Link 到 Tip Link 的运动轨迹。
举例
以一个机械臂为例:
- Base Link: 机械臂的底座部分,可能是与地面固定的框架。
- Tip Link: 如果机械臂的末端是一个夹具,那么这个夹具的位置就是 Tip Link。
在 MoveIt! 的设置中,您提到的参数具有特定的含义和功能。以下是每个参数的解释:
1. Group Name: arm
- 定义: 这是规划组指定的名称。在这个例子中,
arm表示该规划组控制的是机器人的手臂。 - 作用: 通过命名规划组,可以在后续的运动规划和控制中方便地引用这一组链接和关节。
2. Kinematic Solver: kdl_kinematics_plugin/KDLKinematicsPlugin
- 定义: 这是所使用的运动学求解器。
KDLKinematicsPlugin是基于 Kinematics and Dynamics Library (KDL) 的运动学求解插件。 - 作用: 它负责计算机器人的正向运动学和逆向运动学。正向运动学用于从关节角度计算末端执行器的位置,而逆向运动学则用于根据目标位置计算所需的关节角度。
3. Kin. Search Resolution: 0.005
- 定义: 这个参数表示在进行运动规划时的搜索分辨率,单位是米(m)。
- 作用: 它定义了在搜索空间中步进的大小。较小的值会导致更精细的搜索,这可能增加计算时间,但能提供更高精度的路径。
4. Kin. Search Timeout (sec): 0.05
- 定义: 这是运动规划过程中允许的最大搜索时间,单位是秒。
- 作用: 如果在 0.05 秒内未找到有效的运动规划,求解器将停止搜索。这可以帮助避免长时间的计算延迟,尤其是在实时应用中,但也可能导致未找到可行的解决方案。
在配置机械臂的末端执行器(End Effector)时,需要填写一些参数
- End Effector Name(末端执行器名称):
- 这是给末端执行器(例如夹爪、工具等)起的名称。
- End Effector Group(末端执行器组):
- 这是将末端执行器归类到特定组中的选项。此组通常用于定义哪些关节或链接与该末端执行器相关。在您的例子中,组名是
gripper。
- 这是将末端执行器归类到特定组中的选项。此组通常用于定义哪些关节或链接与该末端执行器相关。在您的例子中,组名是
- Parent Link(父链接):
- 这是末端执行器连接到的父链接。通常,这是机械臂的一部分,负责控制末端执行器的位置和姿态。在例子中,父链接为
grasping_frame,这可能是机械臂的一个特定链接,用于抓取物体。
- 这是末端执行器连接到的父链接。通常,这是机械臂的一部分,负责控制末端执行器的位置和姿态。在例子中,父链接为
- Parent Group(父组, 可选项):
- 这是一个可选字段,如果希望将末端执行器与某个特定的组关联,可以在这里填写。若不需要特别设置,此项可以留空
roslaunch moveit_setup_assistant setup_assistant.launch
要在source ./devel/setup.bash的终端使用
学长您好,我看您的【ROS-Moveit!】机械臂控制探索学机械臂联合仿真,但是您开源的代码为啥在运行:
roslaunch pigot_moveit_config moveit_planning_execution.launch
后,rviz显示出错呀,
woc,noetic版本的压根就不用改,新建其他功能包,直接用demo_gazebo.launch,要不然你猜为什么moveit的配置助手会生成关于gazebo的文件,为什么生成gazebo的urdf,就是让你用的,怪不得显示不了xacro模型
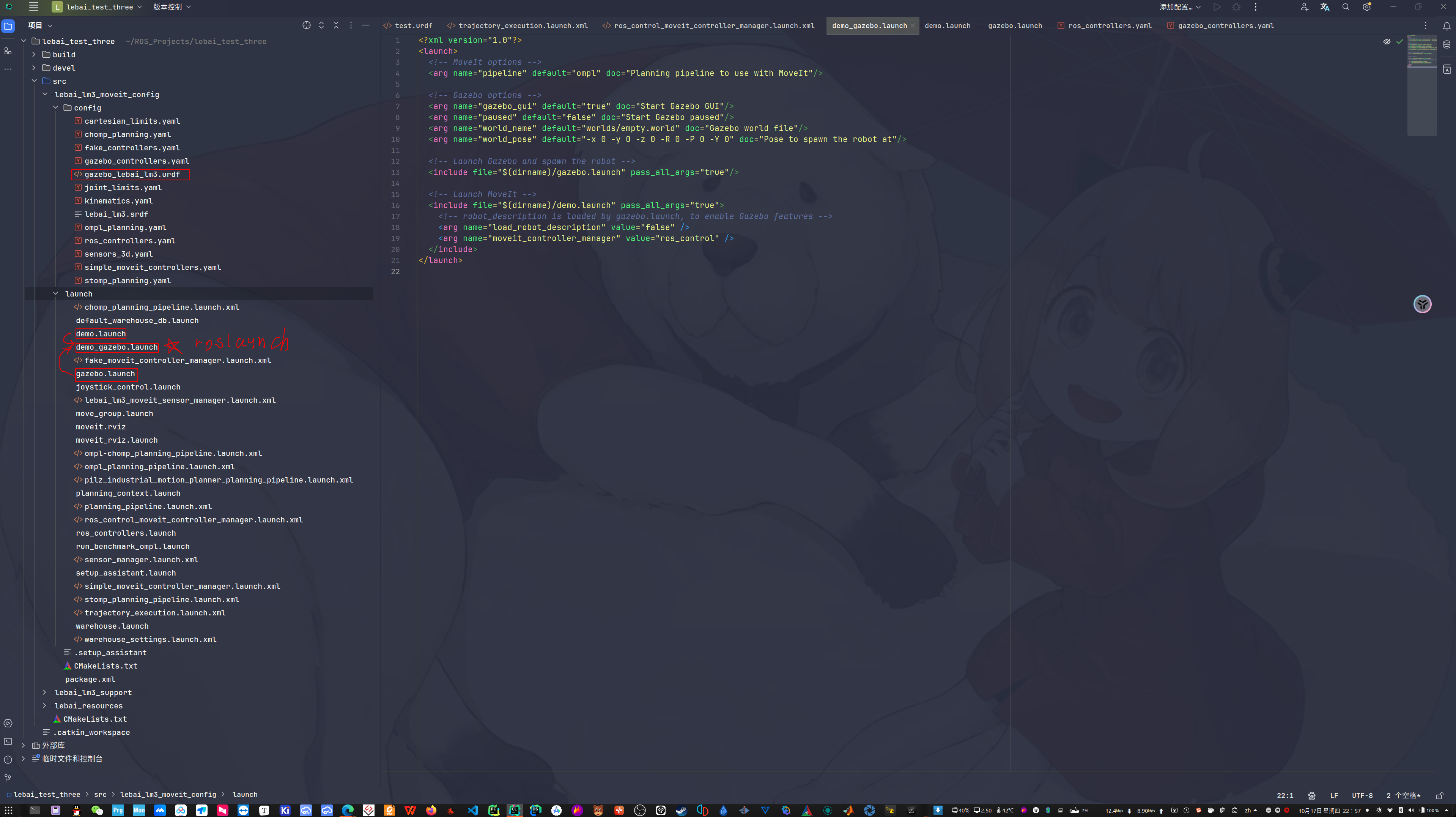
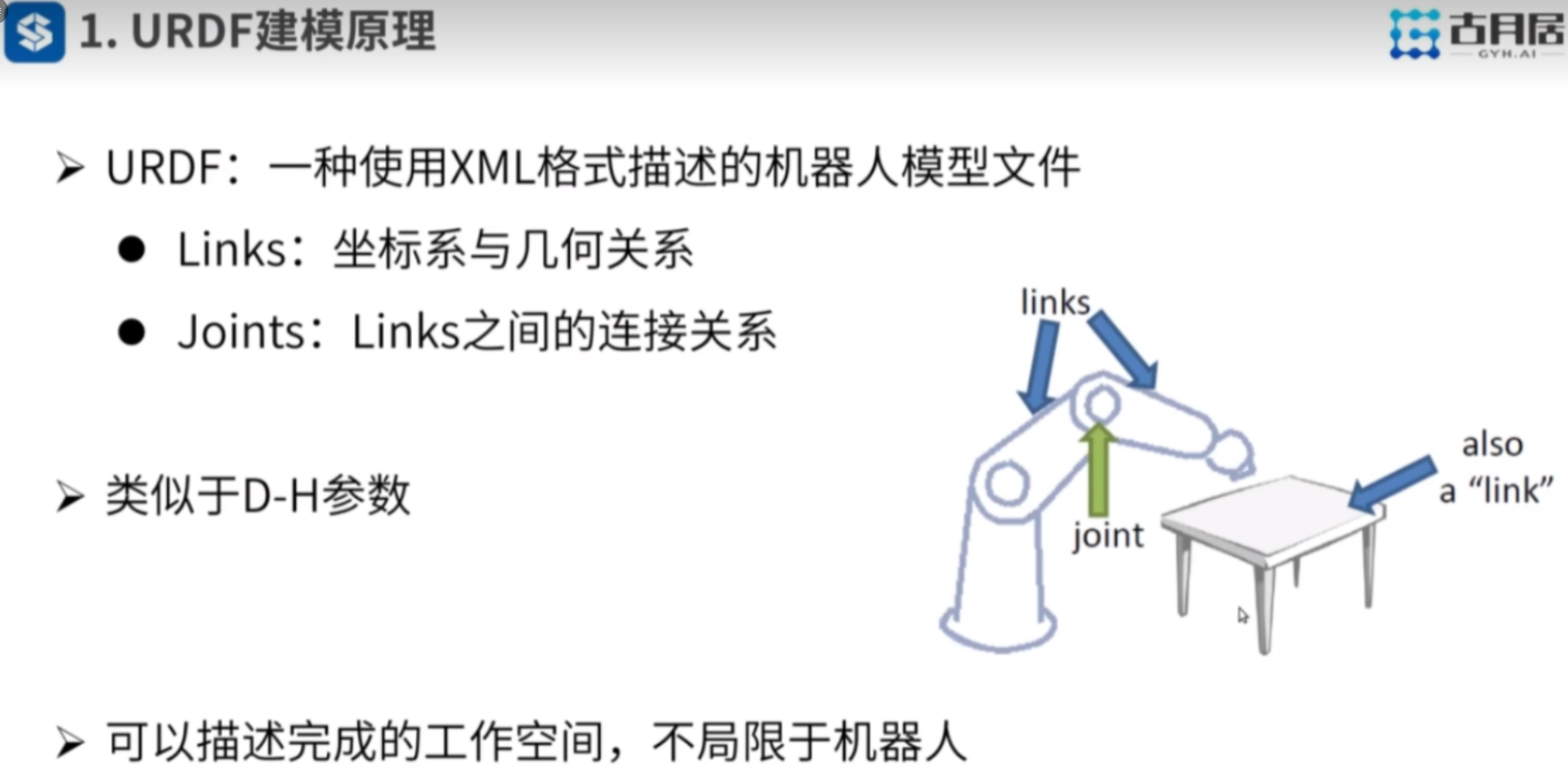
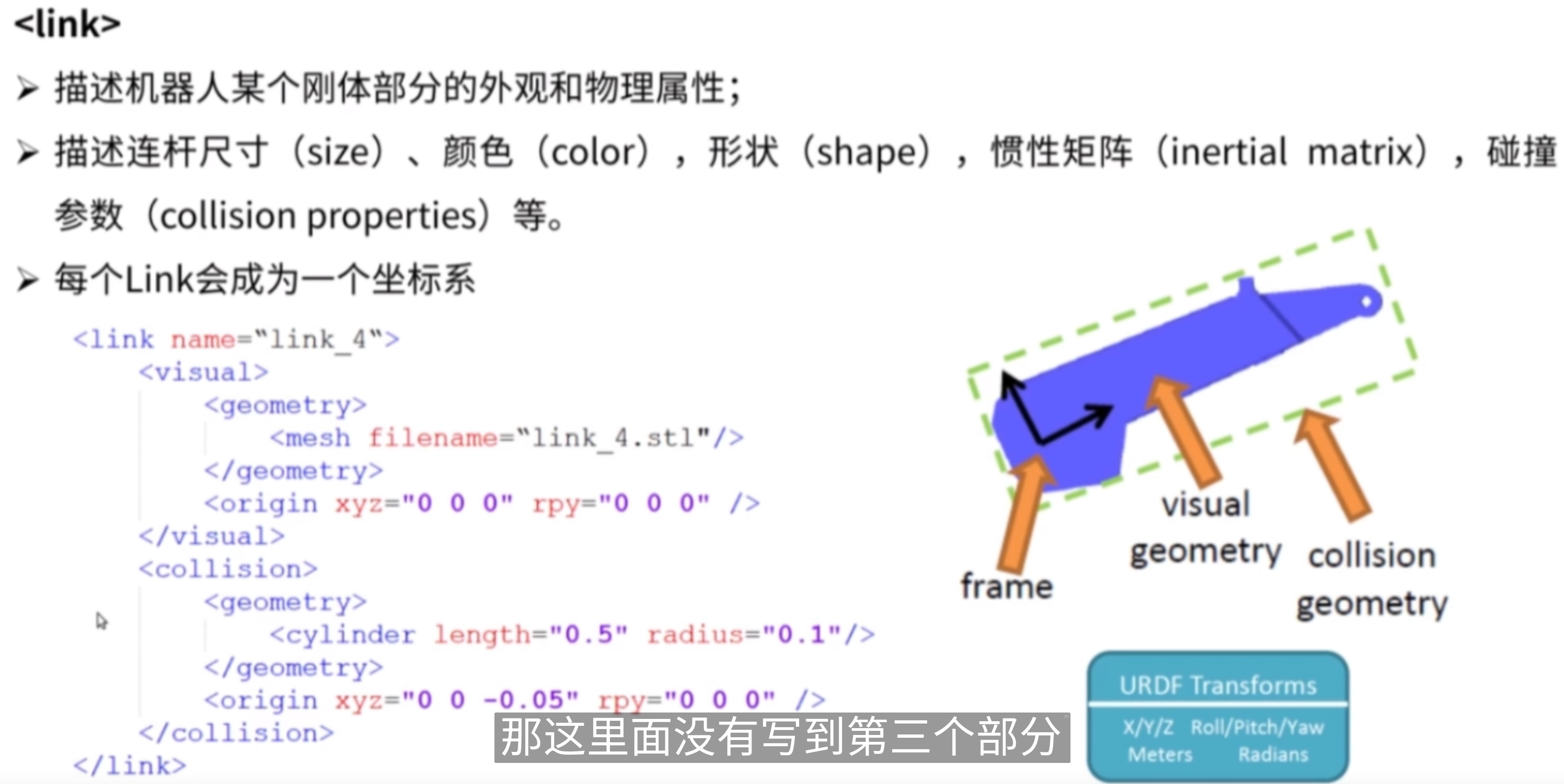

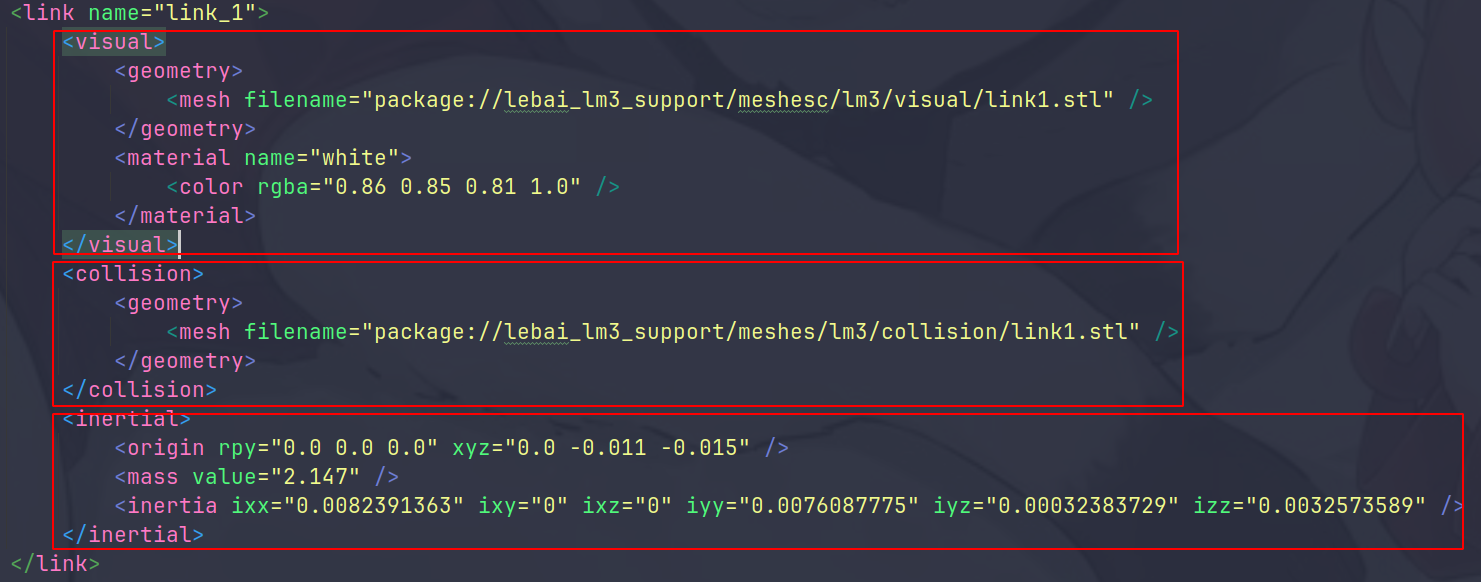 1.
1. <visual>
定义机器人的可视化外观,主要包括几何形状和材质。
<geometry>: 指定连接的几何形状。在这个示例中,使用了一个网格文件(STL格式)来定义link_1的形状。该文件的路径是:Copy Codepackage://lebai_lm3_support/meshesc/lm3/visual/link1.stl<material>: 定义连接的材质和颜色。在此示例中,材质名为white,并且设置了RGBA颜色值(红、绿、蓝、透明度)为(0.86, 0.85, 0.81, 1.0)。这意味着连接的颜色为一种淡灰色,完全不透明。
2. <collision>
这一部分描述连接的碰撞模型,它与可视化模型通常是不同的。碰撞模型用于物理仿真,确保机器人在模拟环境中与其他物体进行碰撞检测。
<geometry>: 这里也使用了一个网格文件,但它的路径是:
Copy Codepackage://lebai_lm3_support/meshes/lm3/collision/link1.stl通常,碰撞模型会比可视化模型简单,以提高仿真性能。
3. <inertial>
这一部分定义了连接的惯性属性,包括质量和转动惯量。惯性属性在机器人运动学和动力学计算中至关重要。
<origin>: 定义了惯性参考点的位置和方向。rpy指的是绕X、Y、Z轴的滚转(roll)、俯仰(pitch)、偏航(yaw)角度,这里均为0.0,表示没有旋转。xyz指的是惯性参考点相对于链接坐标系的位置,这里是(0.0, -0.011, -0.015)。<mass>: 定义连接的质量,这里为2.147 kg。<inertia>: 定义连接的转动惯量矩阵。ixx、iyy和izz分别表示绕X、Y、Z轴的转动惯量,而ixy、ixz和iyz是关于这些轴的耦合项



下次淘宝下单不要付款,先放弃付款,然后再付款的时候有几率跳出“付款再减XX元”,应该是后台店铺给的,香!!!








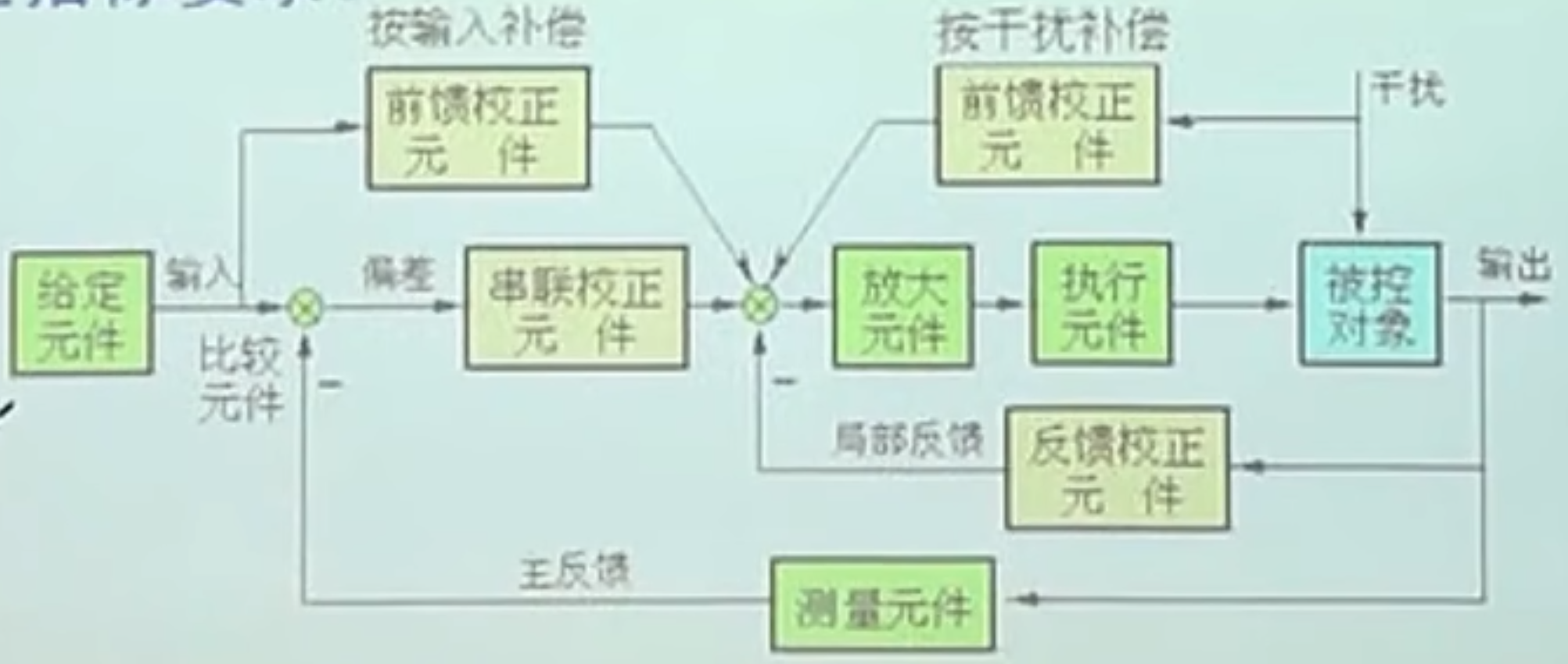
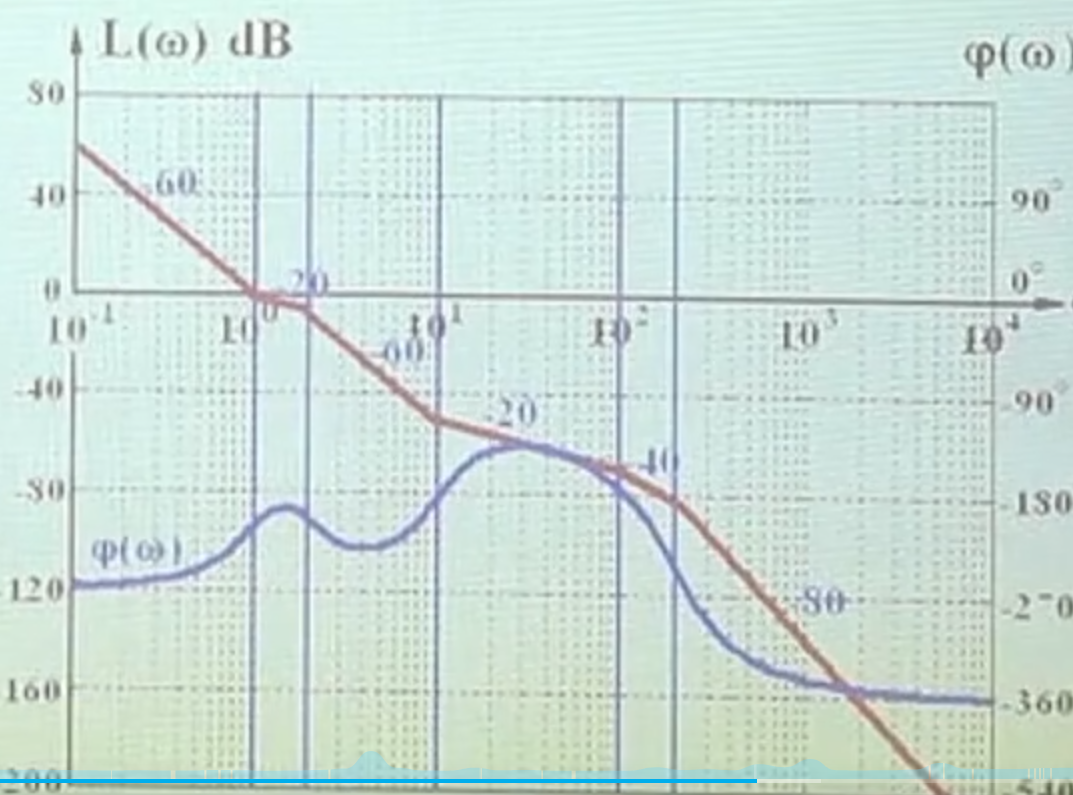


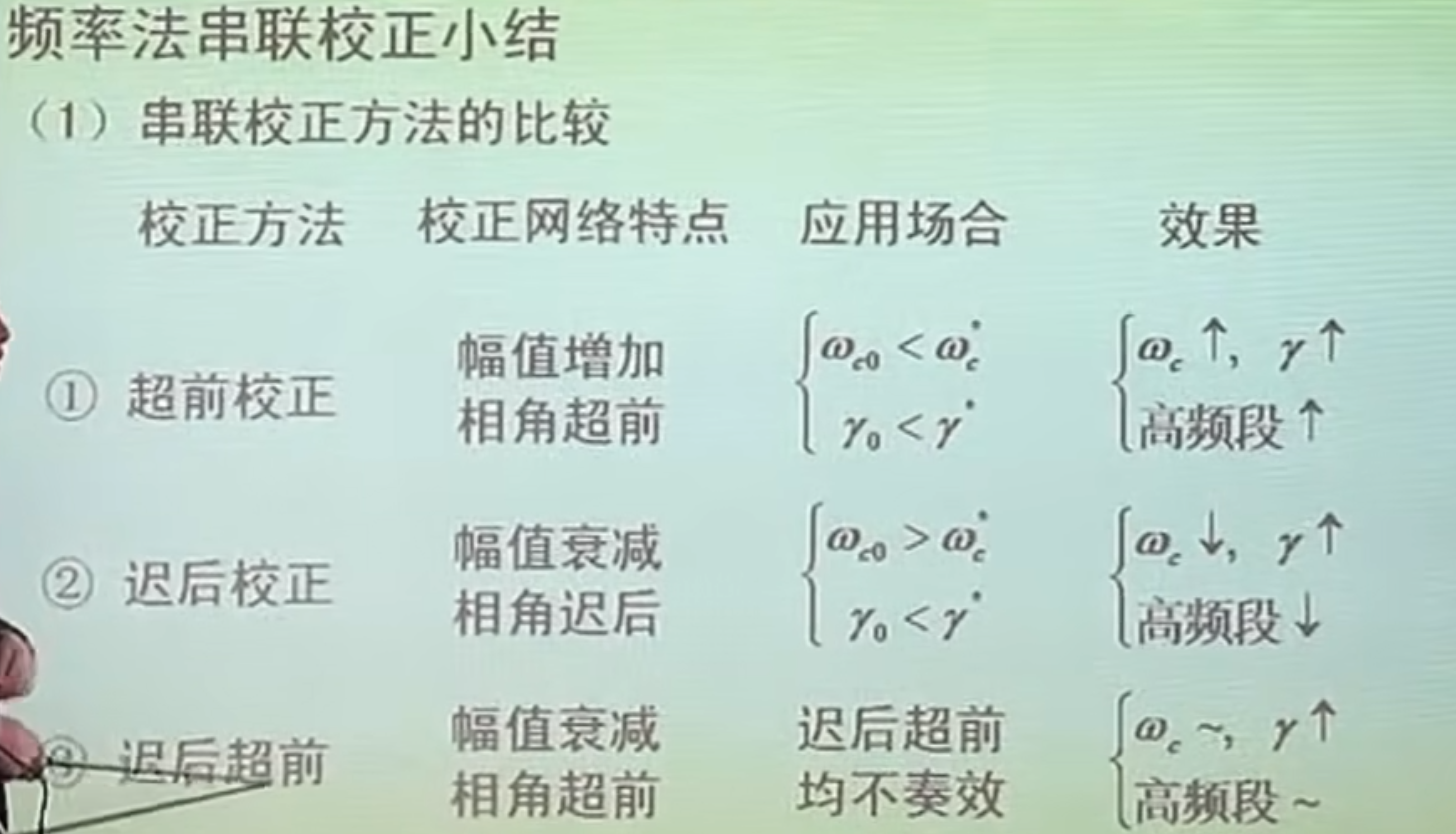
pid校正可以看成迟后超前的特例