OpenGL

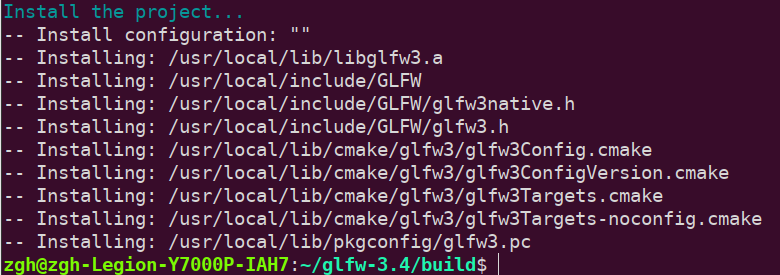
image-20240517165248939

image-20240517165400128

https://www.cnblogs.com/jiujiubashiyi/p/16429717.html

GLFW,GLAD,opengl是什么，有什么联系

GLFW、GLAD和OpenGL是计算机图形学中常用的三个库，它们之间存在着紧密的联系：

  1. OpenGL：是一个跨语言、跨平台的编程接口，用于渲染2D、3D向量图形。它是由硅谷图形公司（Silicon Graphics, SGI）在1992年开发的。OpenGL是图形硬件制造商的标准，也是创作高质量计算机图形的基本工具。OpenGL提供了一个非常灵活的编程接口，让开发者能够利用它来渲染图形。
  2. GLFW：是一个跨平台的OpenGL应用程序接口（API）的多线程窗口和输入管理器。简单来说，GLFW用来创建窗口、处理输入事件（如键盘、鼠标点击等），并管理OpenGL上下文。它使得开发者可以比较容易地创建一个OpenGL环境，因为它简化了OpenGL程序中许多繁琐的设置步骤。
  3. GLAD：是一个自动生成OpenGL函数指针的库。在OpenGL中，许多操作需要通过指针来调用函数，而在不同的操作系统和硬件平台上，这些函数指针的位置可能会有所不同。GLAD就是用来处理这些函数指针的，它会根据当前的平台和OpenGL的版本自动生成对应的函数指针。这为开发者减少了处理这些底层细节的麻烦。

它们之间的联系：

  • 使用OpenGL之前，需要创建一个OpenGL环境，这个环境包括一个窗口以及一个上下文，这是通过GLFW来完成的。
  • GLAD用来确保所有的OpenGL函数调用都能够正确地指向相应的函数，这样开发者就不需要手动查找和设置这些函数指针了。
  • 通常，一个OpenGL程序的设置流程是这样的：首先初始化GLFW，然后使用GLFW创建一个窗口和OpenGL上下文，接着使用GLAD自动加载OpenGL函数，最后就可以开始使用OpenGL进行绘图了。

综上，GLFW和GLAD都是帮助开发者更简单、更有效地使用OpenGL的辅助工具。通过它们，开发者可以专注于图形内容的创作，而不必担心底层的细节问题。

glfwMakeContextCurrent(window);是什么意思

glfwMakeContextCurrent(window); 是一行来自 GLFW（OpenGL Framework）库的代码。GLFW 是一个跨平台的库，用于窗口和输入处理，它使得创建 OpenGL 应用程序变得更加容易。

这句代码的作用是将 OpenGL 渲染上下文关联到由 window 参数指定的窗口。在 OpenGL 中，渲染上下文是用来进行图形绘制的环境，它定义了一系列可以用来配置和控制渲染行为的设置。

在创建窗口之后，必须调用 glfwMakeContextCurrent 函数来指定哪个窗口的上下文将被当前的线程使用。只有当前上下文中的 OpenGL 调用才会对指定的窗口产生影响。如果没有激活任何上下文，任何 OpenGL 调用都会导致错误。

简单来说，当你想要在特定的窗口上绘制图形时，你需要确保该窗口的 OpenGL 上下文被设置为当前上下文。这就是 glfwMakeContextCurrent(window); 这行代码的目的。

gladLoadGLLoader((GLADloadproc)glfwGetProcAddress) 是什么意思

gladLoadGLLoader 是一个函数，通常在 C 或 C++ 程序中使用，用于初始化 OpenGL 函数指针。OpenGL 是一个用于渲染2D和3D矢量图形的跨语言、跨平台的应用程序编程接口（API）。gladLoadGLLoader 函数是 GLAD 库的一部分，GLAD 是一个小型且易于使用的库，它负责在每次调用 OpenGL 函数之前，动态地加载和绑定正确的 OpenGL 函数指针。

glfwGetProcAddress 是另一个函数，属于 GLFW 库（一个用于创建窗口、输入处理等的前端库，常与OpenGL一起使用）。glfwGetProcAddress 的作用是获取指向特定OpenGL函数的指针，该函数在OpenGL核心或者扩展中定义。

gladLoadGLLoader((GLADloadproc)glfwGetProcAddress)

这表示在初始化GLAD库时，它将使用GLFW库提供的函数指针来加载OpenGL函数。这允许应用程序使用OpenGL函数，而不需要关心底层的具体实现细节。

这种机制的好处是，应用程序只需要链接到一个库（比如GLFW），而GLFW会负责查找和加载正确的OpenGL函数。这样做可以简化应用程序的编写和维护工作，同时也确保了应用程序可以轻松地与不同平台的OpenGL版本兼容。

双缓冲(Double Buffer)

应用程序使用单缓冲绘图时可能会存在图像闪烁的问题。 这是因为生成的图像不是一下子被绘制出来的，而是按照从左到右，由上而下逐像素地绘制而成的。最终图像不是在瞬间显示给用户，而是通过一步一步生成的，这会导致渲染的结果很不真实。为了规避这些问题，我们应用双缓冲渲染窗口应用程序。前缓冲保存着最终输出的图像，它会在屏幕上显示；而所有的的渲染指令都会在后缓冲上绘制。当所有的渲染指令执行完毕后，我们交换(Swap)前缓冲和后缓冲，这样图像就立即呈显出来，之前提到的不真实感就消除了。

  • 顶点数组对象：Vertex Array Object，VAO
  • 顶点缓冲对象：Vertex Buffer Object，VBO
  • 元素缓冲对象：Element Buffer Object，EBO 或 索引缓冲对象 Index Buffer Object，IBO

在OpenGL中，任何事物都在3D空间中，而屏幕和窗口却是2D像素数组，这导致OpenGL的大部分工作都是关于把3D坐标转变为适应你屏幕的2D像素.3D坐标转为2D坐标的处理过程是由OpenGL的图形渲染管线（Graphics Pipeline，大多译为管线，实际上指的是一堆原始图形数据途经一个输送管道，期间经过各种变化处理最终出现在屏幕的过程）管理的。图形渲染管线可以被划分为两个主要部分：第一部分把你的3D坐标转换为2D坐标，第二部分是把2D坐标转变为实际的有颜色的像素。(图形渲染管线接受一组3D坐标，然后把它们转变为你屏幕上的有色2D像素输出)

图形渲染管线可以被划分为几个阶段，每个阶段将会把前一个阶段的输出作为输入。所有这些阶段都是高度专门化的（它们都有一个特定的函数），并且很容易并行执行。正是由于它们具有并行执行的特性，当今大多数显卡都有成千上万的小处理核心，它们在GPU上为每一个（渲染管线）阶段运行各自的小程序，从而在图形渲染管线中快速处理你的数据。这些小程序叫做着色器(Shader)。

OpenGL着色器是用OpenGL着色器语言(OpenGL Shading Language, GLSL)写成的

img

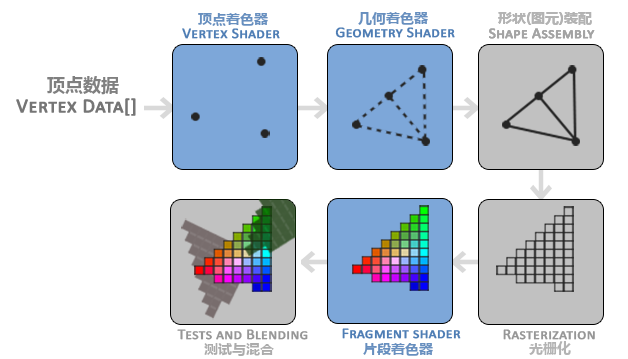
为了让OpenGL知道我们的坐标和颜色值构成的到底是什么，OpenGL需要你去指定这些数据所表示的渲染类型。我们是希望把这些数据渲染成一系列的点？一系列的三角形？还是仅仅是一个长长的线？做出的这些提示叫做**图元(Primitive)**，任何一个绘制指令的调用都将把图元传递给OpenGL。这是其中的几个：GL_POINTS、GL_TRIANGLES、GL_LINE_STRIP。

图形渲染管线的第一个部分—-顶点着色器

把3D坐标转为另一种3D坐标

几何着色器

一组顶点作为输入，这些顶点形成图元，并且能够通过发出新的顶点来形成新的(或其他)图元来生成其他形状

图元装配

将顶点着色器（或几何着色器）输出的所有顶点作为输入（如果是GL_POINTS，那么就是一个顶点），并将所有的点装配成指定图元的形状

光栅化阶段

把图元映射为最终屏幕上相应的像素，生成供片段着色器(Fragment Shader)使用的**片段(Fragment)**。在片段着色器运行之前会执行裁切(Clipping)。裁切会丢弃超出你的视图以外的所有像素，用来提升执行效率。

OpenGL中的一个片段是OpenGL渲染一个像素所需的所有数据

片段着色器

片段着色器的主要目的是计算一个像素的最终颜色

Alpha测试和混合(Blending)阶段

这个阶段检测片段的对应的深度（和模板(Stencil)）值（后面会讲），用它们来判断这个像素是其它物体的前面还是后面，决定是否应该丢弃。这个阶段也会检查alpha值（alpha值定义了一个物体的透明度）并对物体进行混合(Blend)。所以，即使在片段着色器中计算出来了一个像素输出的颜色，在渲染多个三角形的时候最后的像素颜色也可能完全不同

GL_ARRAY_BUFFER目标用于表示顶点属性数据的缓冲区对象

在OpenGL中，VAO（Vertex Array Object）和VBO（Vertex Buffer Object）是用于管理顶点数据的重要概念，并且它们之间存在一定的关系。

  1. VAO（Vertex Array Object）：
    • VAO是OpenGL中用于存储顶点属性状态的对象。它包含了多个指向VBO的指针，用于指定顶点属性数据的格式、排列方式等。
    • VAO可以看作是对VBO的管理器，它记录了OpenGL如何解释顶点数据，包括顶点的位置、颜色、法线等信息。通过绑定VAO，可以轻松地切换顶点属性的设置，从而简化渲染流程。
  2. VBO（Vertex Buffer Object）：
    • VBO是用于存储顶点数据的缓冲区对象。它可以存储顶点的位置、颜色、纹理坐标等信息。
    • 通过将顶点数据存储在VBO中，可以有效地管理和传输大量的顶点数据，而不必反复传输到GPU。

关系：

  • VBO存储了实际的顶点数据，例如顶点的位置、颜色、纹理坐标等。
  • VAO描述了顶点数据的格式和布局，它指明了如何从VBO中读取顶点数据以供渲染使用。
  • 通常情况下，我们先创建和绑定VAO，然后配置相应的VBO，并将VBO与VAO关联。这样，在渲染时只需绑定相应的VAO即可，OpenGL就会根据VAO中的配置自动获取正确的顶点数据进行渲染。

总结来说，VAO用于管理顶点属性状态，而VBO用于存储实际的顶点数据。它们共同协作，使得在OpenGL中管理和使用顶点数据变得更加灵活和高效。

我们可以绘制两个三角形来组成一个矩形（OpenGL主要处理三角形）

着色器(Shader)是运行在GPU上的小程序。这些小程序为图形渲染管线的某个特定部分而运行。从基本意义上来说，着色器只是一种把输入转化为输出的程序。着色器也是一种非常独立的程序，因为它们之间不能相互通信；它们之间唯一的沟通只有通过输入和输出。

Uniform是另一种从我们的应用程序在 CPU 上传递数据到 GPU 上的着色器的方式，但uniform和顶点属性有些不同。首先，uniform是全局的(Global)。全局意味着uniform变量必须在每个着色器程序对象中都是独一无二的，而且它可以被着色器程序的任意着色器在任意阶段访问。第二，无论你把uniform值设置成什么，uniform会一直保存它们的数据，直到它们被重置或更新。

在OpenGL中，VBO（Vertex Buffer Object）和VAO（Vertex Array Object）都是用于管理顶点数据的对象。它们之间的联系和区别如下：

联系：

  • VBO和VAO都是用于管理顶点属性数据的对象。
  • 它们都可以通过OpenGL API进行创建、绑定、更新和删除等操作。
  • VAO可以保存多个VBO的绑定状态，使得我们在绘制时只需绑定VAO即可同时启用多个顶点属性数组。

区别：

  • VBO是用于存储和管理顶点数据的缓冲对象，包括顶点位置、法线、颜色、纹理坐标等属性数据。它能够提高渲染效率，因为可以将这些数据上传到显卡内存中，而不需要每次绘制时都从系统内存中获取。
  • VAO是用于管理VBO的绑定状态的对象，它记录了VBO的绑定状态以及每个属性在VBO中的偏移量、类型等信息。VAO可以看作是一组VBO的绑定描述符，它规定了如何从VBO中获取顶点属性数据。

总体来说，VBO和VAO在OpenGL中都扮演着非常重要的角色，它们都可以提高渲染效率，使得开发者可以更加方便地管理和操作顶点属性数据。其中，VBO主要用于存储和管理顶点数据，而VAO则是用于在绘制时快速激活和绑定多个顶点属性数组。

把两个角度都发送

试一下发后两个数据，看看是不是数据的问题

试试发5个

image-202406031552098552024.6.3.15.52Matlab报错，遂改，无用！！！！

艺术家和程序员更喜欢使用纹理(Texture)。纹理是一个2D图片（甚至也有1D和3D的纹理），它可以用来添加物体的细节.这样就可以让物体非常精细而不用指定额外的顶点

为了能够把纹理映射(Map)到三角形上，我们需要指定三角形的每个顶点各自对应纹理的哪个部分。这样每个顶点就会关联着一个纹理坐标(Texture Coordinate)，用来标明该从纹理图像的哪个部分采样（译注：采集片段颜色）。之后在图形的其它片段上进行片段插值(Fragment Interpolation)。

使用 Xlib 来获取窗口大小需要一些底层的操作，但可以通过以下步骤来实现：

首先，你需要安装 python-xlib 库。你可以使用以下命令在 Ubuntu 上安装：

sudo apt-get install python-xlib

然后，你可以使用下面的代码来获取当前活动窗口的大小：

from Xlib import display

def get_screen_size():
    disp = display.Display()
    screen = disp.screen()
    root_win = screen.root
    windowID = root_win.get_full_property(disp.intern_atom('_NET_ACTIVE_WINDOW'), 0).value[0]
    window = disp.create_resource_object('window', windowID)
    geometry = window.get_geometry()
    return geometry.width, geometry.height

width, height = get_screen_size()
print("Window size: {} x {}".format(width, height))

这段代码中，我们首先创建了一个 Display 对象，然后获取了当前活动窗口的 ID。接着，我们使用这个窗口 ID 创建了一个 window 对象，并通过这个对象的 get_geometry 方法获取了窗口的宽度和高度。

请注意，使用 Xlib 需要对 X 窗口系统有一定的了解，因为它是一个底层的库，直接和 X 服务器进行交互。希望这个示例能够帮助你开始使用 Xlib 来获取窗口大小。

  • layout(location=0): 这是一个着色器布局限定符（layout qualifier），用于指定顶点属性在输入阶段的位置。在这里，location=0 表示顶点属性的位置索引为 0。这个位置索引将与顶点数组对象（VAO）中的对应属性绑定，以确保正确地将顶点数据传递给顶点着色器。
  • in: 这是一个输入变量修饰符，用于指示这个变量是从外部传递给顶点着色器的。
  • vec3: 这是指定变量类型的关键字，表示这个变量是一个三维向量。
  • in_position: 这是变量的名称，用于在顶点着色器中引用这个输入变量。在这里，in_position 可能表示顶点的位置信息。

在OpenGL中，gl_Position是一个内置的变量，用于表示顶点着色器（Vertex Shader）输出的顶点位置。它是一个四维向量（vec4），表示顶点的齐次坐标（Homogeneous Coordinates），通常用于表示三维空间中的点。齐次坐标是四维的，其中前三个分量表示点的位置，而第四个分量通常被用于表示点的类型或者进行透视除法（Perspective Division）。在顶点着色器中，对 gl_Position 的设置将影响后续的图元装配（Primitive Assembly）和光栅化（Rasterization）阶段，最终确定绘制的像素位置。因此，正确设置 gl_Position 是绘制正确图形的关键。

[[ 0.5 0.5 0. 0. 1. 0. ]
[-0.5 0.5 0. 1. 0. 0. ]
[-0.5 -0.5 0. 0. 0. 1. ]
[ 0.5 0.5 0. 0. 1. 0. ]
[-0.5 -0.5 0. 0. 0. 1. ]
[ 0.5 -0.5 0. 1. 0. 0. ]]

layout(location=0) in vec3 in_position;
layout(location=1) in vec3 in_color;

self.vbo_format = '3f 3f'
self.attrs = ('in_position', 'in_color')

vertex_data = np.hstack([vertices_array, colors_array])

缩放

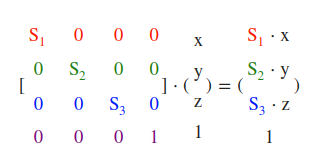
image-20240608192337289

位移

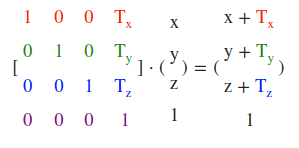
image-20240608192358635

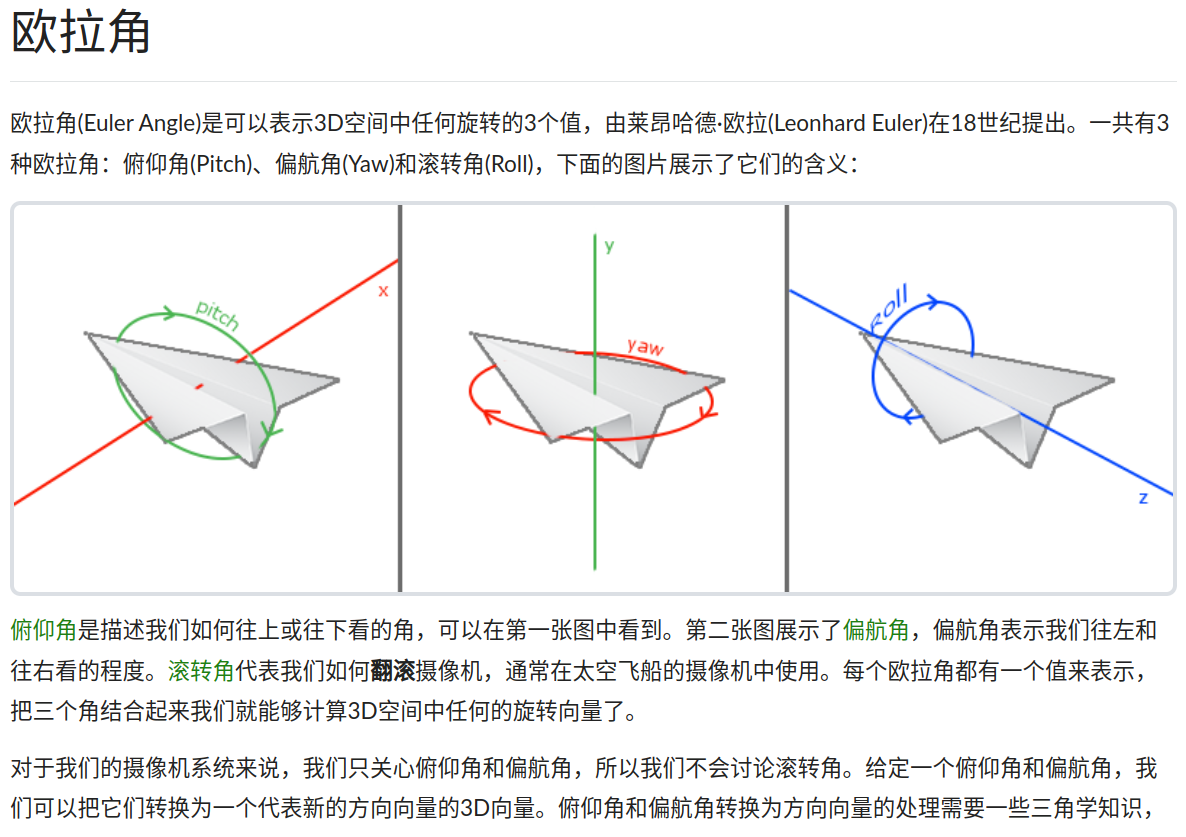
大多数旋转函数需要用弧度制的角，但幸运的是角度制的角也可以很容易地转化为弧度制的：

  • 弧度转角度：角度 = 弧度 * (180.0f / PI)
  • 角度转弧度：弧度 = 角度 * (PI / 180.0f)

image-20240608192525938

我这一辈子，抠抠搜搜的花了很多钱，精精明明的上了很多当。骂骂咧咧的干了很多活，小心翼翼的闯了很多祸。精打细算的欠了一屁股帐。认认真真的范了很多错。掏心掏肺的结了很多仇。不明不白的吃了很多亏。窝窝囊囊的活了几十年。

  1. glm::mat4 trans;：首先声明了一个4x4的矩阵trans，用于表示变换矩阵。
  2. trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));：这一行代码对trans进行了旋转变换。使用了glm库中的rotate函数，将trans矩阵绕Z轴旋转90度（使用radians函数将角度转换为弧度），并将结果赋值给trans本身。
  3. trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));：接着对trans进行了缩放变换。使用了glm库中的scale函数，将trans矩阵沿着X、Y、Z三个轴分别缩放0.5倍，并将结果再次赋值给trans本身。
  • 局部空间(Local Space，或者称为物体空间(Object Space))
  • 世界空间(World Space)
  • 观察空间(View Space，或者称为视觉空间(Eye Space))
  • 裁剪空间(Clip Space)
  • 屏幕空间(Screen Space)

为了将坐标从一个坐标系变换到另一个坐标系，我们需要用到几个变换矩阵，最重要的几个分别是模型(Model)、观察(View)、投影(Projection)三个矩阵。我们的顶点坐标起始于局部空间(Local Space)，在这里它称为局部坐标(Local Coordinate)，它在之后会变为世界坐标(World Coordinate)，观察坐标(View Coordinate)，裁剪坐标(Clip Coordinate)，并最后以屏幕

坐标(Screen Coordinate)的形式结束。下面的这张图展示了整个流程以及各个变换过程做了什么：

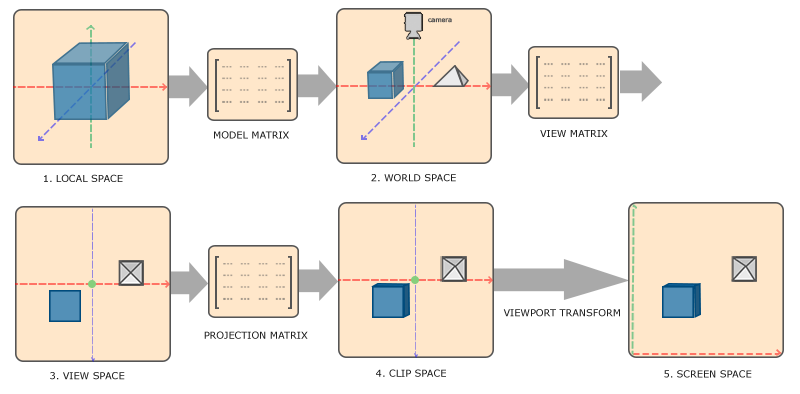
coordinate_systems

  1. 局部坐标是对象相对于局部原点的坐标，也是物体起始的坐标。
  2. 下一步是将局部坐标变换为世界空间坐标，世界空间坐标是处于一个更大的空间范围的。这些坐标相对于世界的全局原点，它们会和其它物体一起相对于世界的原点进行摆放。
  3. 接下来我们将世界坐标变换为观察空间坐标，使得每个坐标都是从摄像机或者说观察者的角度进行观察的。
  4. 坐标到达观察空间之后，我们需要将其投影到裁剪坐标。裁剪坐标会被处理至-1.0到1.0的范围内，并判断哪些顶点将会出现在屏幕上。
  5. 最后，我们将裁剪坐标变换为屏幕坐标，我们将使用一个叫做视口变换(Viewport Transform)的过程。视口变换将位于-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器，将其转化为片段。

你可能已经大致了解了每个坐标空间的作用。我们之所以将顶点变换到各个不同的空间的原因是有些操作在特定的坐标系统中才有意义且更方便。例如，当需要对物体进行修改的时候，在局部空间中来操作会更说得通；如果要对一个物体做出一个相对于其它物体位置的操作时，在世界坐标系中来做这个才更说得通，等等。如果我们愿意，我们也可以定义一个直接从局部空间变换到裁剪空间的变换矩阵，但那样会失去很多灵活性。

局部空间——–模型矩阵——–世界空间———观察矩阵———-观察空间(摄像机空间)———–投影矩阵————–裁剪空间————–视口变换————-屏幕空间

image-20240609164419389

image-20240609164929887

image-20240609165058873

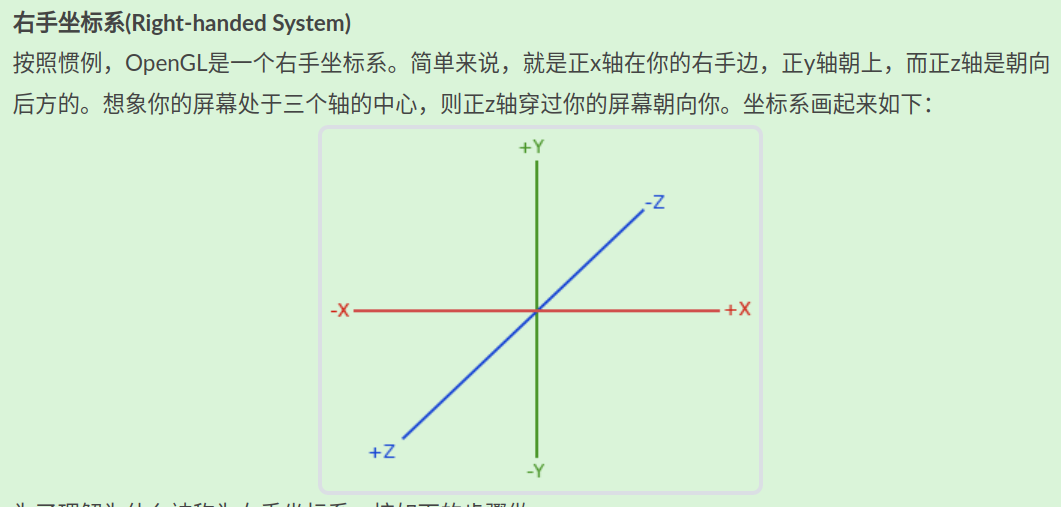
image-20240609211854570

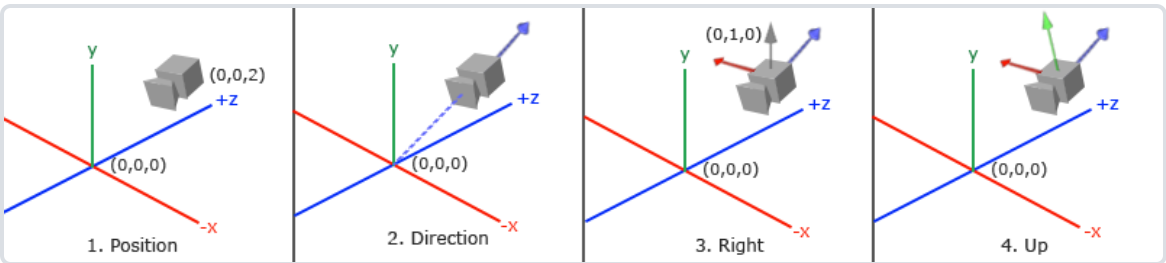
image-20240609212927721

image-20240609213514370

glm::LookAt函数需要一个位置、目标和上向量。它会创建一个观察矩阵。

为了改变摄像机方向

image-20240609221012736

self.m_projection=glm.perspective(V_FOV,ASPECT_RATIO,NEARPLANE,FARPLANE)

使用 GLM 库中的 glm::perspective() 函数创建了一个投影矩阵（projection matrix）.会根据给定的参数创建一个透视投影矩阵，并返回这个矩阵。这个投影矩阵描述了从摄像机位置观察场景时的投影效果，将三维场景转换为二维屏幕空间

image-20240610000155256

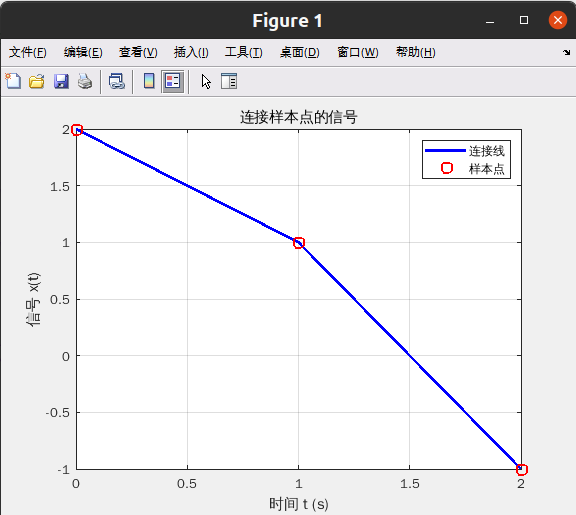
对连续时间正弦信号考虑下面表示式：
x ( t ) = s i n ( 2 π f 0 t + φ )
可以按抽样频率 fs=1/Ts对 x(t)抽样来获得离散时间信号
x [ n ] = x ( t )|t =nTs = x ( t ) |t=n / fs = s i n ( 2 πf0 /fsn + φ ),
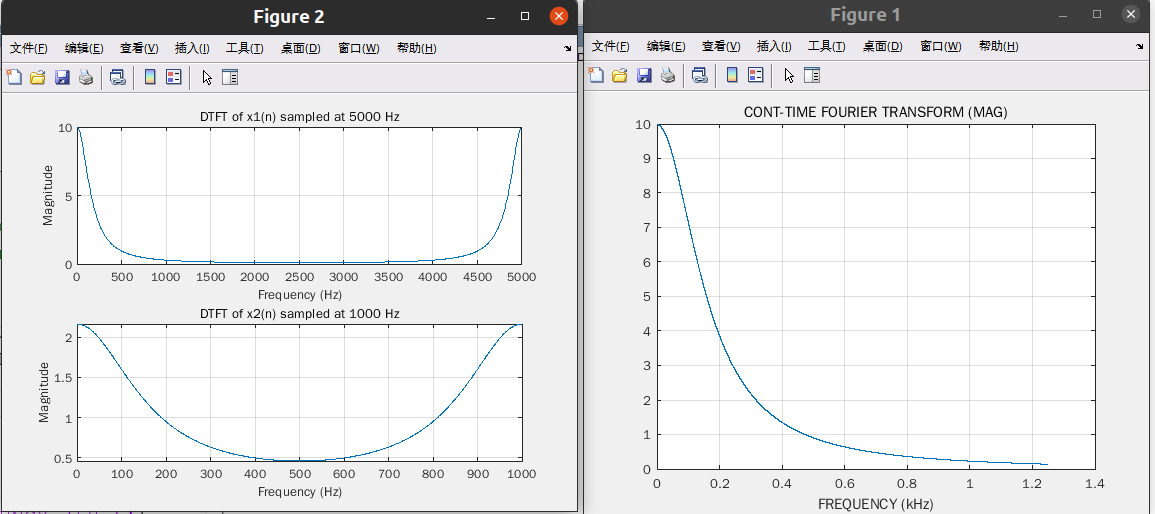
f0 =500Hz， fs 取 100Hz， 绘出 x[n]及其 DTFT

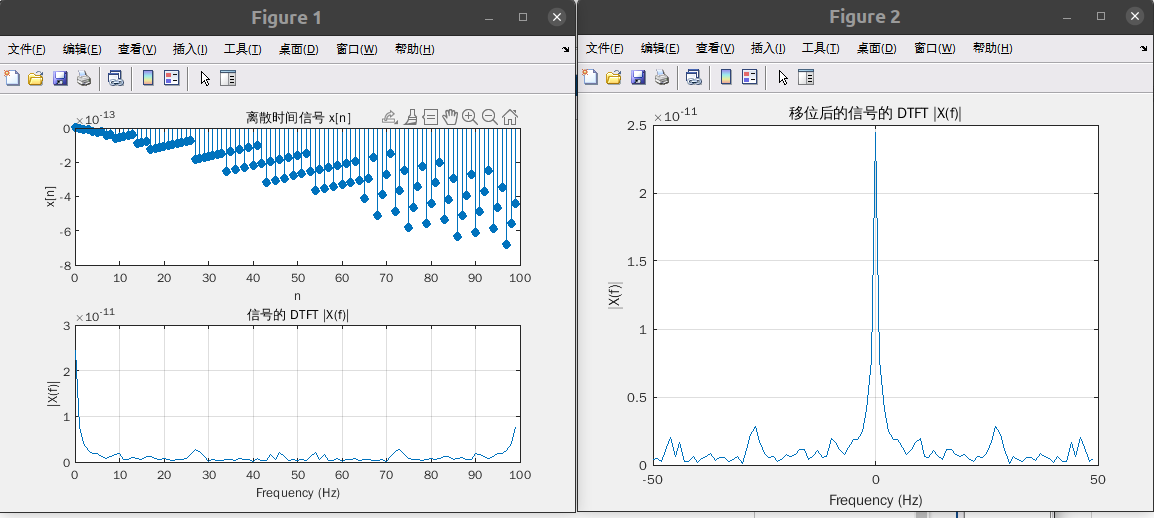
image-20240611133720092

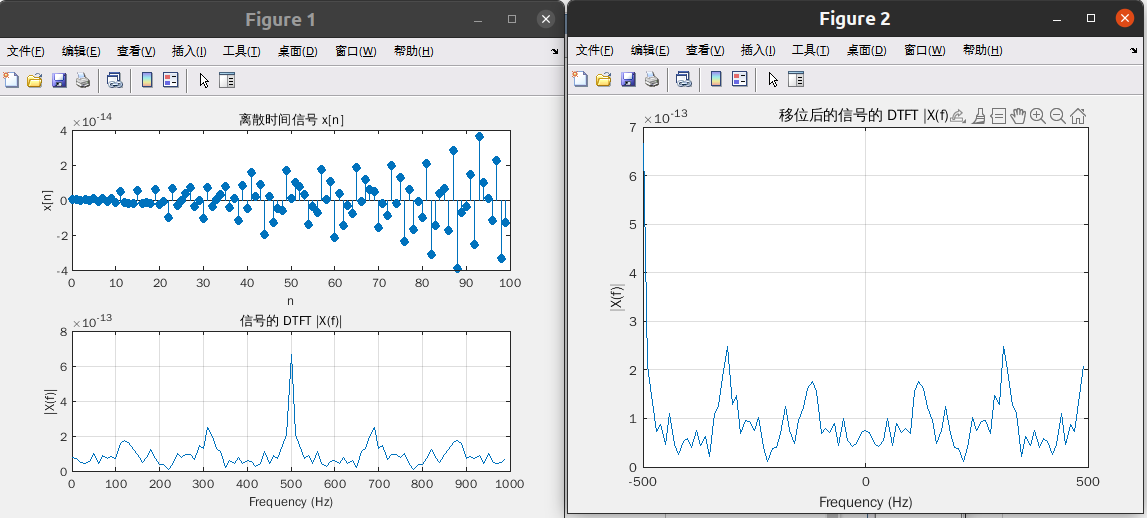
image-20240611133805550

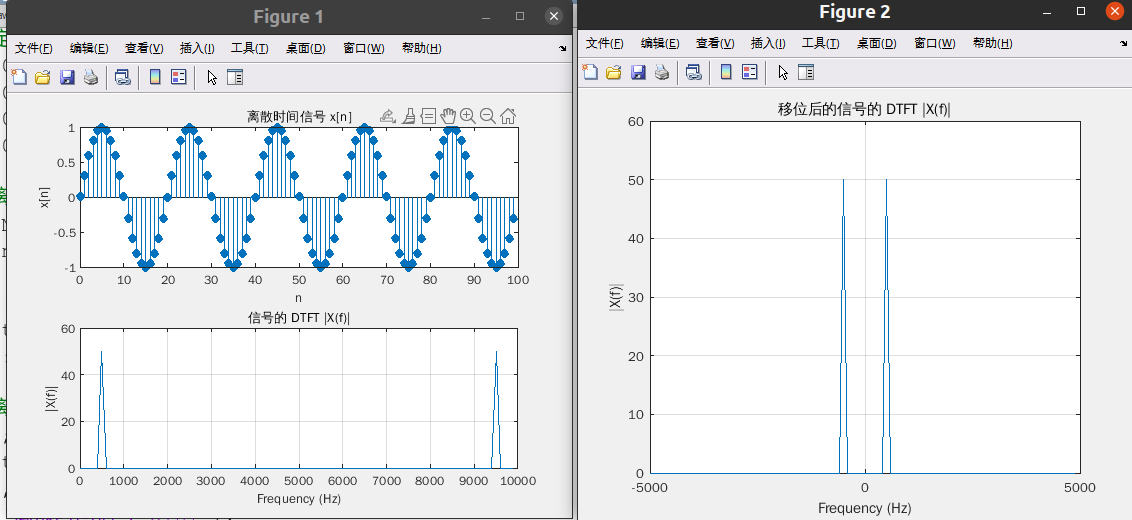
image-20240611133838091

image-20240611140046801

以 5000HZ 和 1000HZ 分别对其采样得到 x1(n)， x2(n)；画出它们的 DTFT 并比较

image-20240611140651535

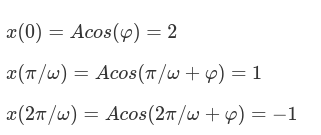
image-20240611141635271

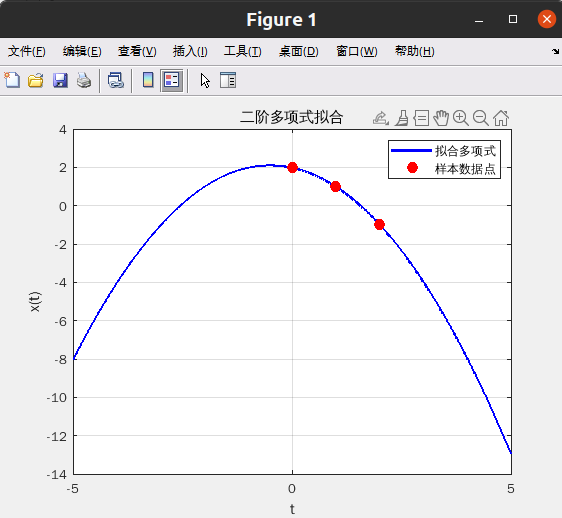
我们可以从第一个方程中直接得到 A 和 φ 的关系：

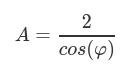
image-20240611141659727

φ ！=π/2+kπ

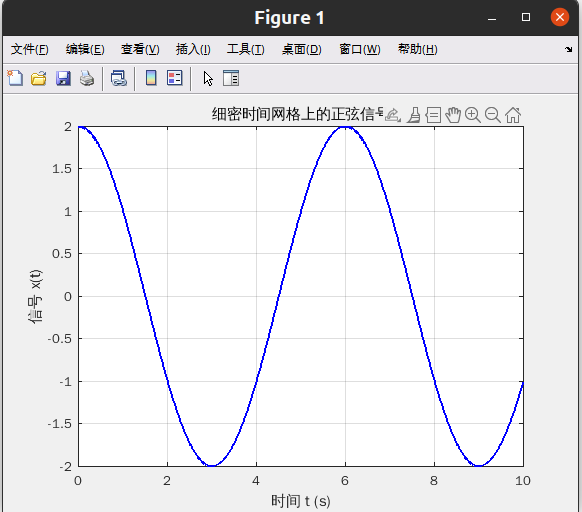
x(t)=2cos(π/3 *t)

image-20240611143342649

image-20240611143614094

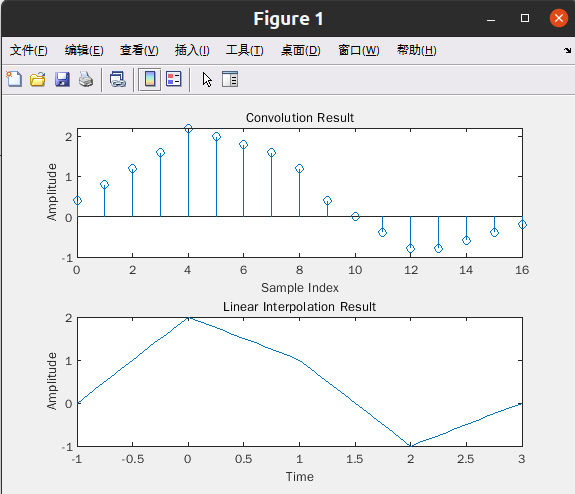
image-20240611144943071

image-20240611145404898

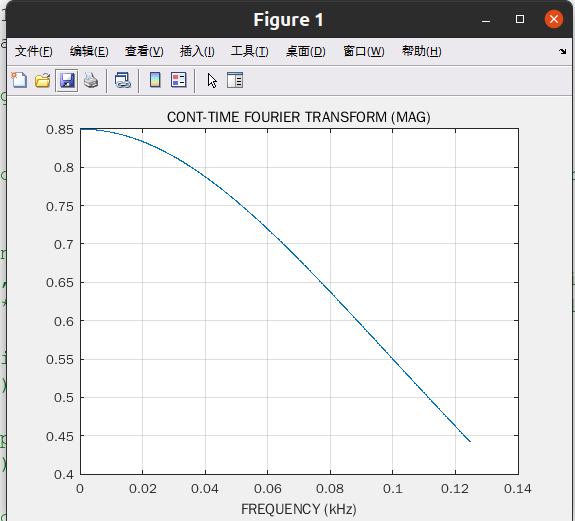
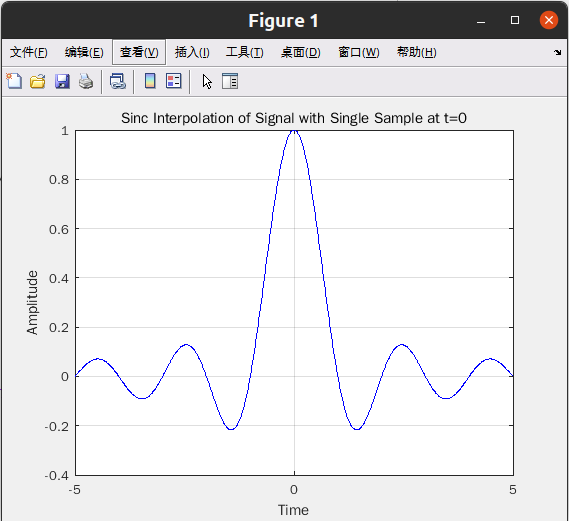
现实中无法实现理想低通滤波器。然而，可以按下面的方法计算由理想低通滤波器产生的
波形：理想低通运算相当于信号频谱与频域的矩形函数相乘，这对应于信号与通过傅里叶逆变
换得到的时域 sinc 函数的卷积。当其应用于点样本时，卷积和为 sinc 函数内插：

xa(t)=sum_{n=-无穷}^{正无穷} [xa(nt) sin(π(t-nTs)/Ts)/(π(t-nTs)/Ts)]

(3.18)
其中，样本 xa(nt)取自 t= nTs处。
a. 假设只有有限数量的信号样本是非零值，且只需在有限时间区间上进行信号重建，写出
基于(3.18)式的 sinc 内插表示式。

syms t n Ts xa;

xa_t = symsum(xa * sin(pi*(t-n*Ts)/Ts)/(pi*(t-n*Ts)/Ts), n, -inf, inf);

image-20240611153315884

C：
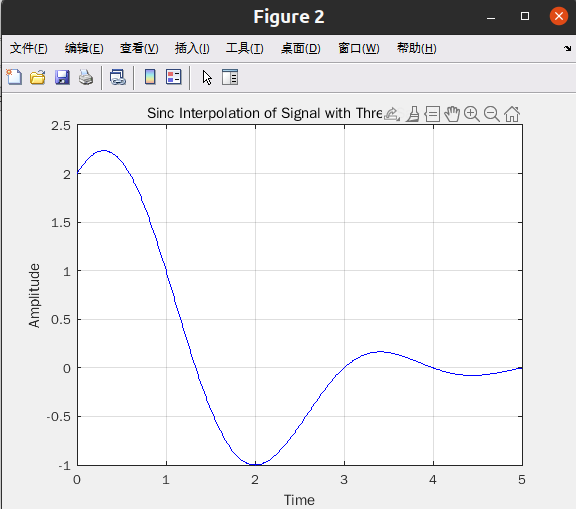
image-20240611155005492

根据奈奎斯特采样定理，要求 fs≥2fbfs≥2fb 以避免混叠现象。因此，fb<fs2fb<2fs 是满足采样定理的条件。

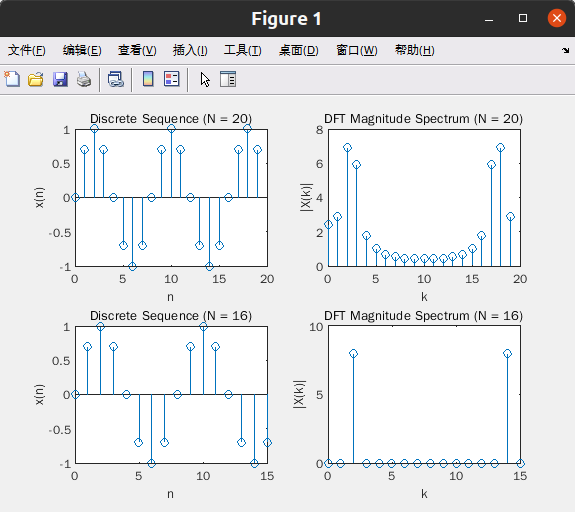
image-20240613162635475

45HZ，基本周期 T是 1/45

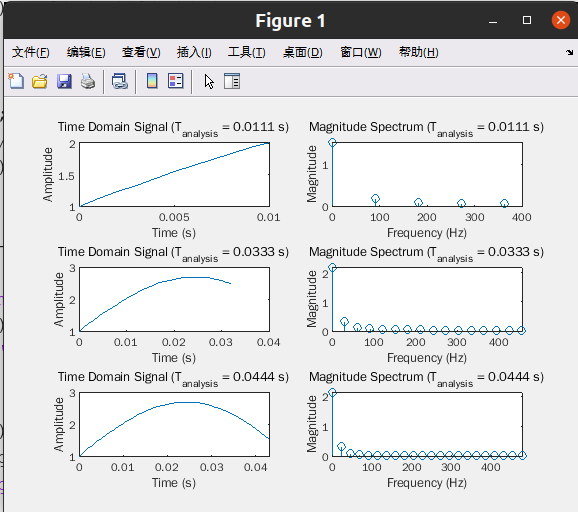
image-20240613160828062

结果分析与总结

  1. 分析长度 ( 0.5T_p = 0.1 ) 秒:
    • 频谱图中的频率分辨率较低，频率成分不清晰，可能会导致频率混淆。
    • 由于分析长度小于一个周期，频谱分析结果可能包含较多的谐波失真和旁瓣效应。
  2. 分析长度 ( 1.5T_p = 0.3 ) 秒:
    • 频谱图中的频率分辨率有所提高，主要频率成分变得更加明显。
    • 由于分析长度超过一个周期，频谱分析结果更加准确，频率成分容易识别。
  3. 分析长度 ( 2T_p = 0.4 ) 秒:
    • 频谱图中的频率分辨率进一步提高，主要频率成分非常清晰。
    • 更长的分析长度提供了更好的频率分辨率，但同时也增加了计算时间和资源需求。

总结

  • 选择合适的分析长度：分析长度可以通过基本周期 ( T_p ) 的整数倍来选择。一般来说，分析长度至少应等于或大于一个周期 ( T_p )，这样可以确保频谱分析结果的准确性。
  • 平衡分辨率和计算复杂度：较长的分析长度提供更好的频率分辨率，但也会增加计算时间和资源。在实际应用中，需要在频率分辨率和计算复杂度之间取得平衡。
  • 避免过短的分析长度：过短的分析长度（例如小于一个周期）可能导致频谱结果混乱，难以准确识别主要频率成分

image-20240613161203147

你可以看到，白色的阳光实际上是所有可见颜色的集合，物体吸收了其中的大部分颜色。它仅反射了代表物体颜色的部分，被反射颜色的组合就是我们所感知到的颜色（此例中为珊瑚红）。

这些颜色反射的定律被直接地运用在图形领域。当我们在OpenGL中创建一个光源时，我们希望给光源一个颜色。在上一段中我们有一个白色的太阳，所以我们也将光源设置为白色。当我们把光源的颜色与物体的颜色值相乘，所得到的就是这个物体所反射的颜色（也就是我们所感知到的颜色）。让我们再次审视我们的玩具（这一次它还是珊瑚红），看看如何在图形学中计算出它的反射颜色。我们将这两个颜色向量作分量相乘，结果就是最终的颜色向量了：

glm::vec3 lightColor(1.0f, 1.0f, 1.0f);
glm::vec3 toyColor(1.0f, 0.5f, 0.31f);
glm::vec3 result = lightColor * toyColor; // = (1.0f, 0.5f, 0.31f);

我们可以看到玩具的颜色吸收了白色光源中很大一部分的颜色，但它根据自身的颜色值对红、绿、蓝三个分量都做出了一定的反射。这也表现了现实中颜色的工作原理。由此，我们可以定义物体的颜色为==物体从一个光源反射各个颜色分量的大小。==

**现实世界的光照是极其复杂的，而且会受到诸多因素的影响，这是我们有限的计算能力所无法模拟的。因此OpenGL的光照使用的是简化的模型，对现实的情况进行近似，这样处理起来会更容易一些，而且看起来也差不多一样。这些光照模型都是基于我们对光的物理特性的理解。其中一个模型被称为冯氏光照模型(Phong Lighting Model)。冯氏光照模型的主要结构由3个分量组成：环境(Ambient)、漫反射(Diffuse)和镜面(Specular)光照。下面这张图展示了这些光照分量看起来的样子：

img

  • 环境光照(Ambient Lighting)：即使在黑暗的情况下，世界上通常也仍然有一些光亮（月亮、远处的光），所以物体几乎永远不会是完全黑暗的。为了模拟这个，我们会使用一个环境光照常量，它永远会给物体一些颜色。
  • 漫反射光照(Diffuse Lighting)：模拟光源对物体的方向性影响(Directional Impact)。它是冯氏光照模型中视觉上最显著的分量。物体的某一部分越是正对着光源，它就会越亮。
  • 镜面光照(Specular Lighting)：模拟有光泽物体上面出现的亮点。镜面光照的颜色相比于物体的颜色会更倾向于光的颜色。

在漫反射光照部分，光照表现并没有问题，这是因为我们没有对物体进行任何缩放操作，所以我们并不真的需要使用一个法线矩阵，而是仅以模型矩阵乘以法线就可以。但是如果你会进行不等比缩放，使用法线矩阵去乘以法向量就是必须的了。

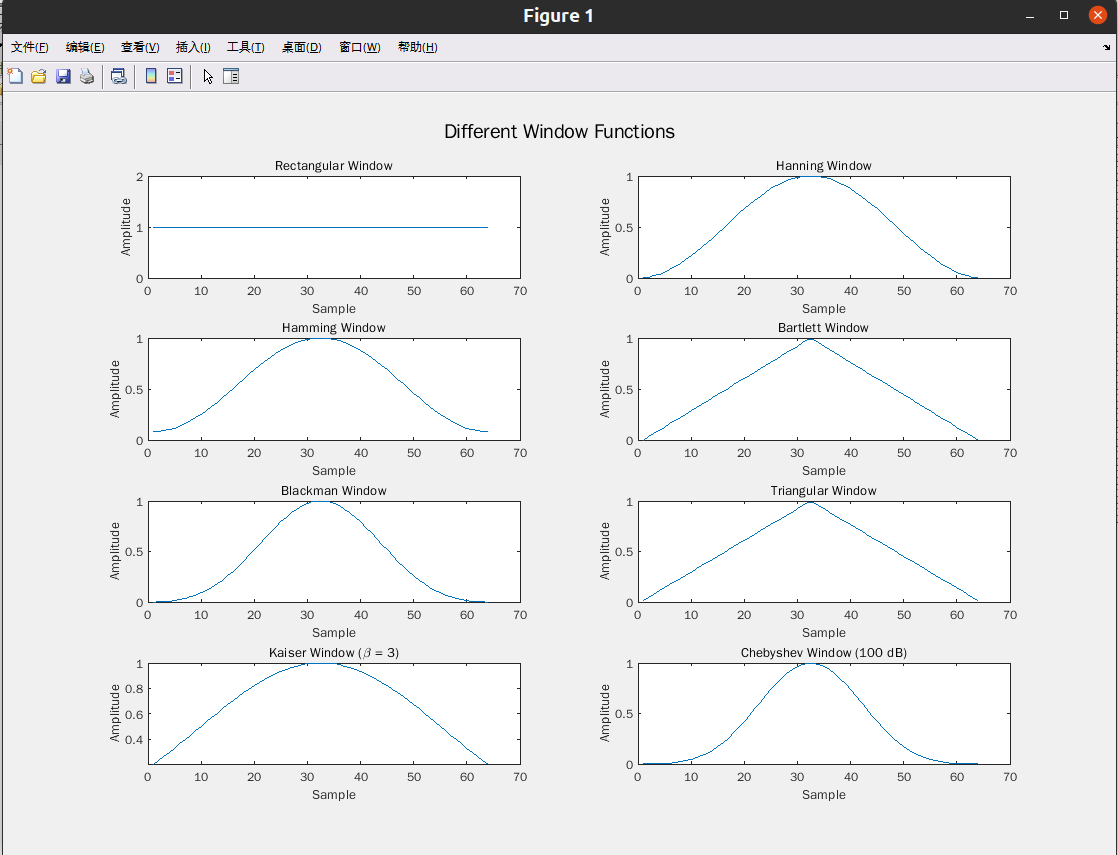
image-20240618134143162

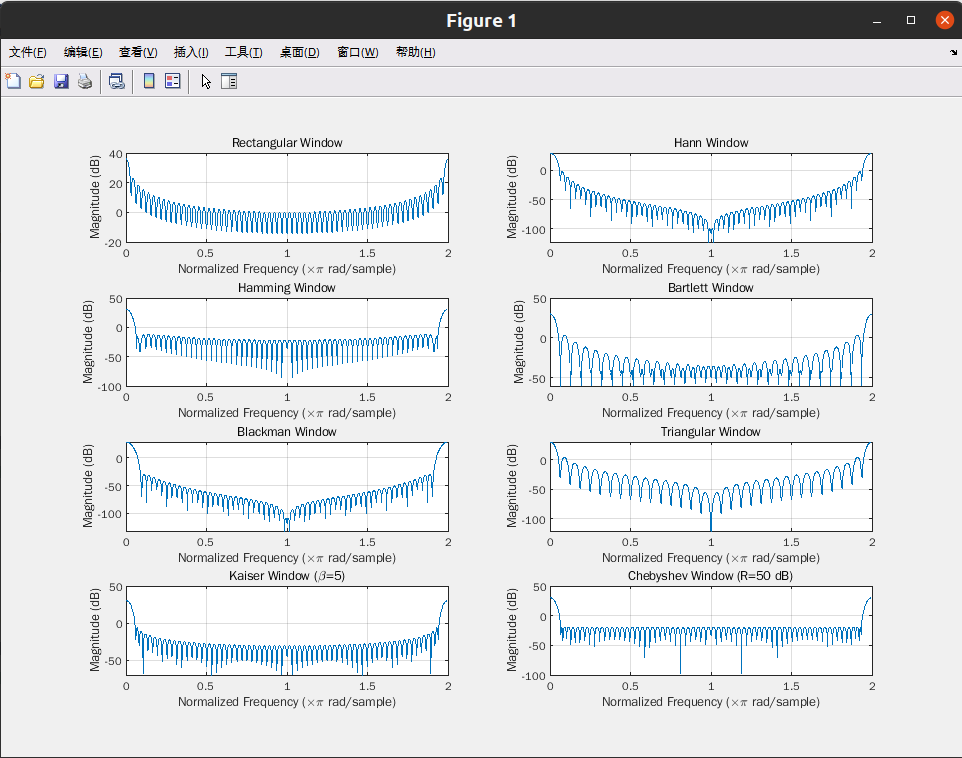
image-20240618134913056

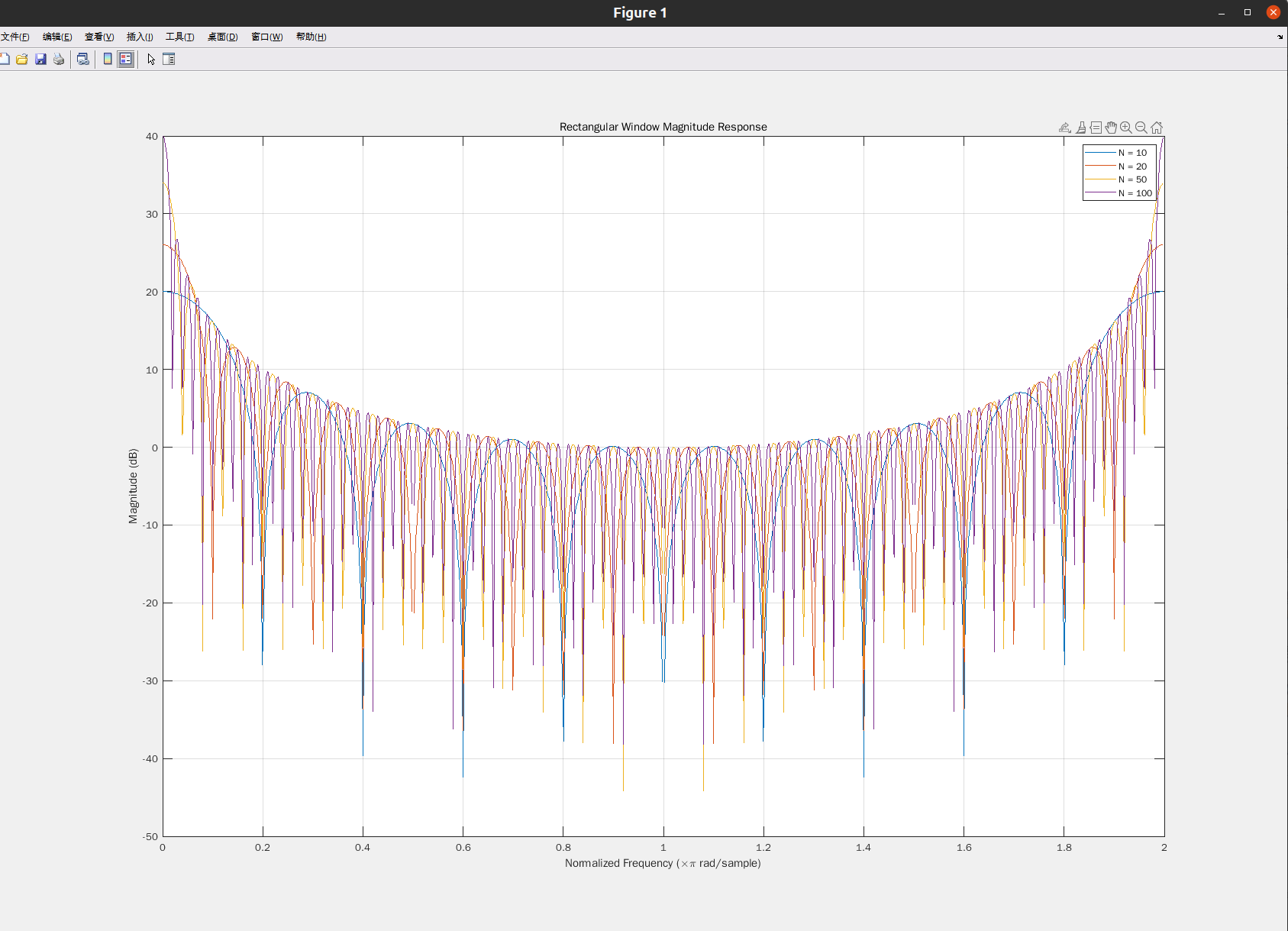
image-20240618135228887

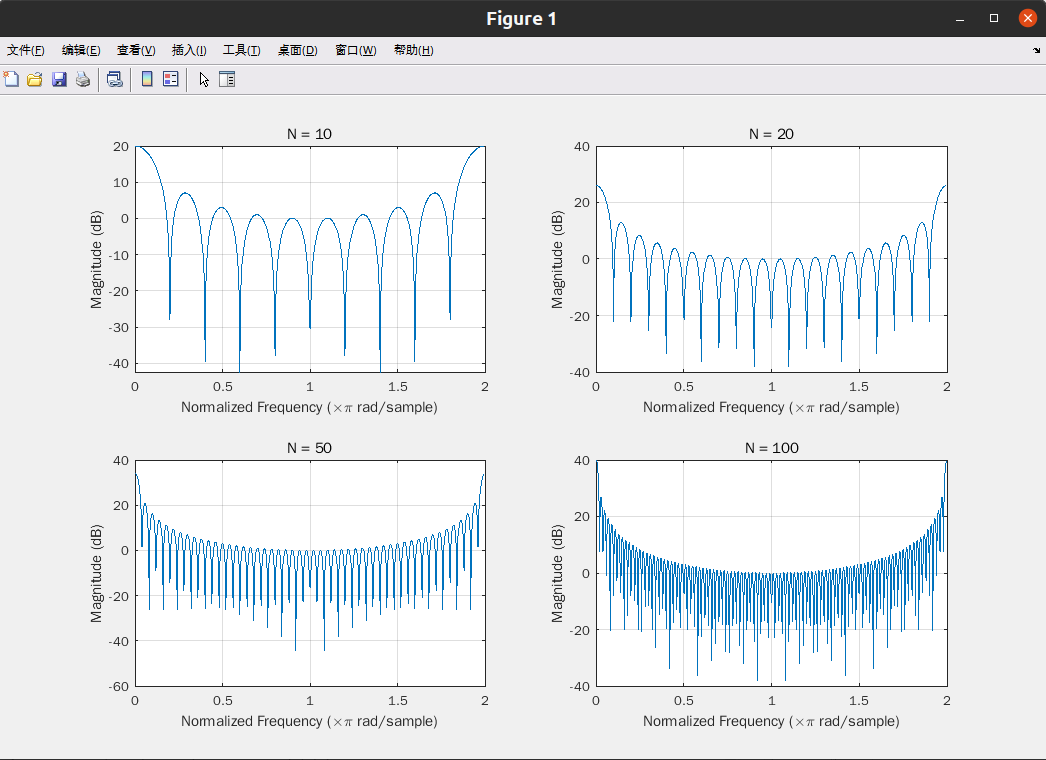
image-20240618135413787

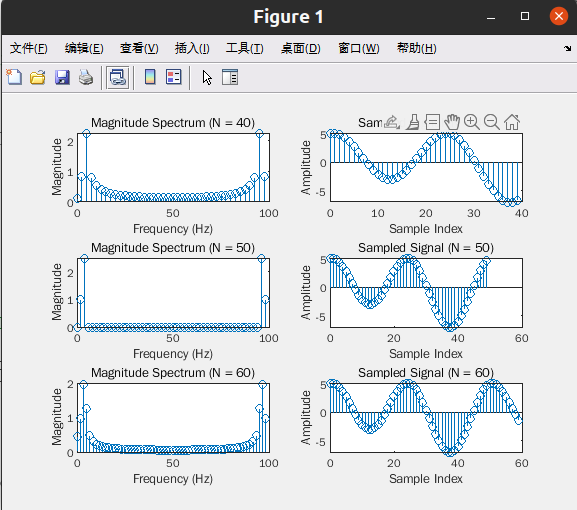
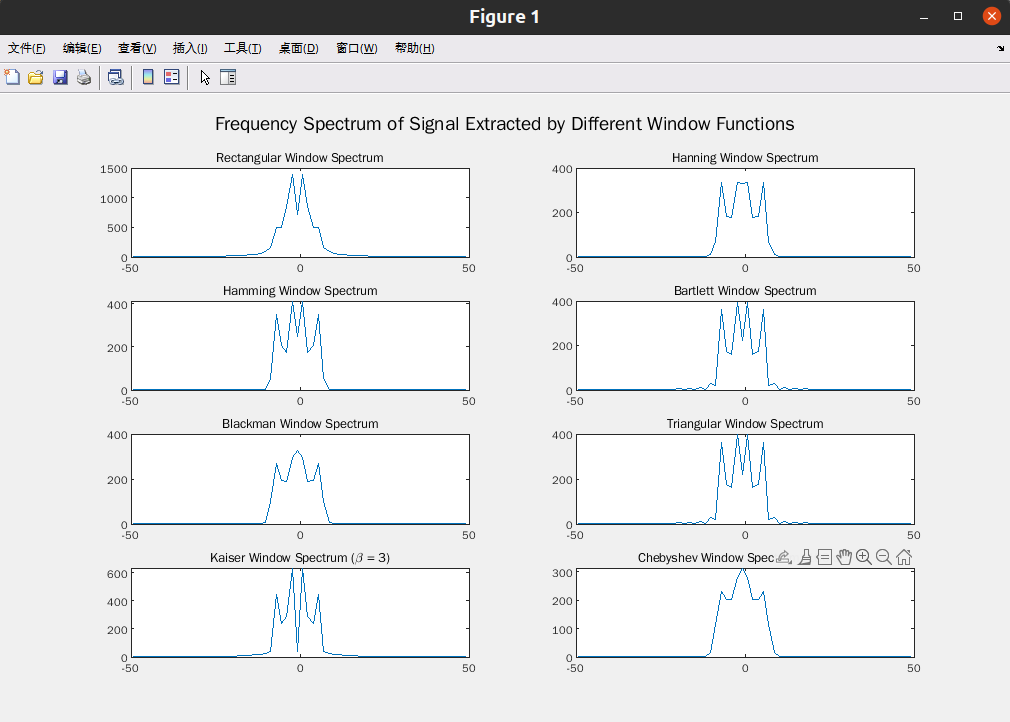
已知周期信号 x(t) = 0.75 + 3.4 cos 2πft + 2.7 cos 4π ft +1.5sin 3.5π ft + 2.5sin 7π ft ，其
中 25/16Hz,若截断时间长度分别为信号周期的 0.9 和 1.1 倍，试分别绘制这八种窗函数
提取的 x(t)的频谱。

image-20240618141855717

根据下列指标采用窗函数法设计低通数字滤波器， 通带截止频率wp= 0.2π ，阻带截止频率

ws = 0.3π，通带最大衰减 0.25dB，阻带最小衰减 50dB。

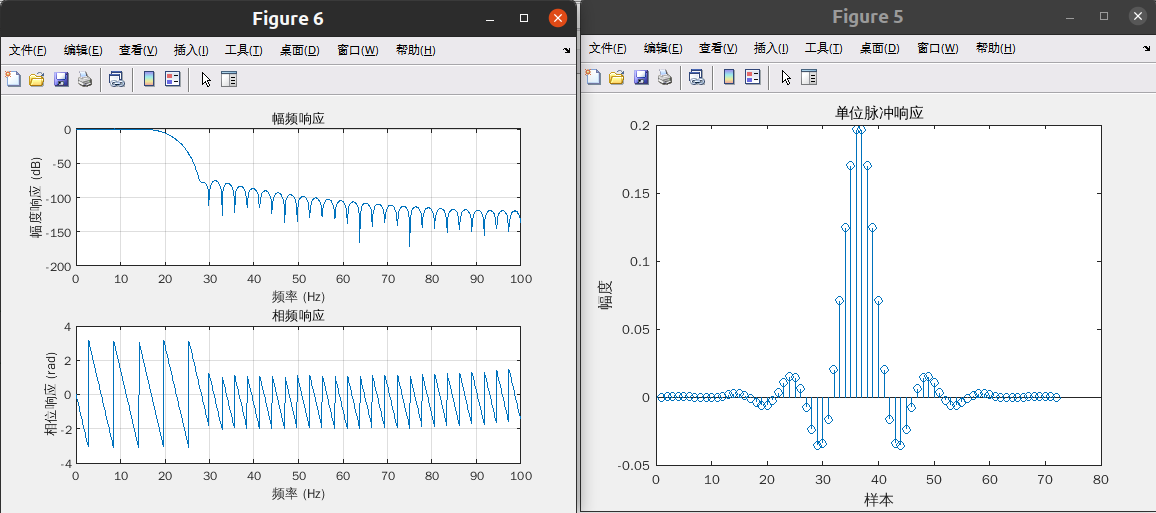
（1） 分别利用汉明窗、布莱克曼窗和凯泽窗设计该滤波器，且滤波器具有线性相位。绘出脉冲响应 h(n)及滤波器的频率响应；

（2） 增加 N，观察过渡带和最大肩峰值的变化。

利用汉明窗设计数字微分器

Hd(e^jw)=

jw,0<w<π;

-jw,-π<w<0.

要求 N = 21，且滤波器具有线性相位。